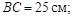 |
Примеры выполнения задач контрольной работы
|
|
|
|
Задача 1
Исходные данные (рисунок 3.9):
; 
; 
;
AC = 15 см, AB = 20 см.
Определить: угловую скорость и угловое ускорение блока 2, линейные скорости и линейные ускорения точек В и С.
Решение
|
1 Выполняем необходимые построения для изображения векторов скоростей. Поскольку блок 2 катится без проскальзывания по нерастяжимой нити PD, то его мгновенный центр скоростей находится в точке Р, как это показано на рисунке 3.10. В соответствии с условием точка Е колеса 1 движется вниз, поэтому вниз движется и точка К блока 2. Следовательно, направление ω2 соответствует вращению по ходу часовой стрелки.
Чтобы определить направления векторов скоростей точек В и С, проводим отрезки, соединяющие эти точки с МЦС. Соответствующие векторы скоростей направляются перпендикулярно этим отрезкам в сторону поворота тела по отношению к точке Р.
2 Определяем угловую скорость блока 2 и линейные скорости точек В и С.
|
.
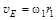Поскольку точки Е и К связаны нерастяжимой нитью, то их линейные скорости одинаковы
.
Скорость точки К может быть выражена через угловую скорость ω2 так:
.
Отсюда
.
В заданный момент времени
.
Теперь можно определить линейные скорости точек В и С:
;
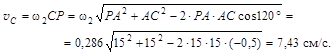
Здесь расстояние ВР определено из прямоугольного треугольника РАВ по теореме Пифагора, а длина СР – по теореме косинусов из треугольника РАС.
3 Рассчитываем угловое ускорение тела 2 и линейные ускорения точек В и С.
При расчете ускорений в качестве полюса следует взять точку, для которой известна траектория. Из схемы механизма видно, что центр блока (точка А) движется вдоль вертикальной прямой. Следовательно, у нее отсутствует нормальное ускорение. Для нахождения ее касательного ускорения следует продифференцировать выражение скорости v A по времени. Эта скорость может быть найдена по формуле
|
|
|
.
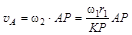Поскольку размеры, входящие в это выражение, не меняются в процессе движения, то при дифференцировании получаем:
.
Ускорение точки В теперь можно определить из выражения
. (3.3)
Значения составляющих ускорения 
и 
находим по формулам:
,
.
Для определения углового ускорения ε2 продифференцируем по времени выражение угловой скорости ω2:
.
Тогда
.
Поскольку движение тела 1 ускоренное (направления ω1 и ε1 совпадают), то вращение блока 2 так же ускоренное. Поэтому направление углового ускорения ε2 такое же, как и угловой скорости ω2. По той же причине вектор ускорения точки А сонаправлен с ее вектором скорости.
|
направляется перпендикулярно отрезку АВ в сторону углового ускорения звена 2, а вектор – от точки В к точке А, как это показано на рисунке 3.11.
Проецируя векторное равенство (3.3) на оси декартовой системы координат, получаем:
Аx: 
,
Аy: 
.
Отсюда полное ускорение точки В
.
Расчет ускорения точки С выполняем по аналогичному с точкой B алгоритму. В качестве полюса используем, по-прежнему, точку А. Тогда
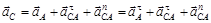; (3.4)
;
.
Векторы 
и 
направляем по тому же правилу, как и векторы и .
Проецируя выражение (3.4) на оси координат, получаем
Аx: 
;
Аy: 
.
Таким образом,
.
Задача 2
Исходные данные: в изображенном на рисунке 3.12 механизме ОА = 10 см, СВ = 10 см. В заданном его положении 
рад/с, 
рад/с2.
|
Решение
1 Выполняем построения для изображения векторов скоростей. Точка А находится на вращающемся теле 1. Поэтому она движется по окружности радиуса ОА, и вектор ее скорости направляется перпендикулярно отрезку ОА в сторону вращения стержня, как это показано на рисунке 3.13. Точка В движется по прямой ОВ. Следовательно, вектор ее скорости должен лежать на этой прямой.
|
|
|
|
Вектор скорости точки А направлен так, что это соответствует повороту звена АВ по ходу часовой стрелки вокруг точки Р. По этому направлению изображаем угловую скорость ω2.
Чтобы показать вектор скорости точки С, соединяем ее с мгновенным центром скоростей (точкой Р). Названный вектор лежит на перпендикуляре к отрезку РС и направлен в сторону угловой скорости ω2.
2 Определяем линейные скорости точек В и С и угловую скорость звена 2.
Кривошип ОА совершает вращательное движение вокруг оси, перпендикулярной плоскости рисунка, поэтому линейная скорость точки А
см/с.
С другой стороны, точка А принадлежит телу 2, которое в данный момент времени совершает поворот вокруг точки Р. Следовательно,
. (3.5)
Для нахождения угловой скорости ω2 следует определить расстояние АР. Из треугольника ОАВ (см. рисунок 3.12), используя теорему синусов, получаем:
;
см;
см.
Из прямоугольного треугольника ОВР (см. рисунок 3.13)
см.
Следовательно, 
см.
Тогда из формулы (3.5) следует, что
рад/с.
Используя выражения, аналогичные (3.5), находим линейные скорости точек В и С:
; 
.
В прямоугольном треугольнике ОВР углы при вершинах О и Р одинаковы. Поэтому 
см. Следовательно,
см/с.
Для определения расстояния РС применим к треугольнику РСВ теорему косинусов. Из нее следует, что
см.
Тогда окончательно находим
см/с.
3 Определяем ускорения точек В и С и угловое ускорение звена 2.
Поскольку заданы угловая скорость и угловое ускорение звена 1, то вначале рассчитаем ускорение точки А. Она движется по окружности, поэтому ее ускорение имеет касательную и нормальную составляющие:
. (3.6)
Касательное ускорение точки А
.
Оно направляется перпендикулярно отрезку ОА в сторону углового ускорения тела, как это показано на рисунке 3.14.
Нормальное ускорение точки А рассчитывается по формуле
см/с2
|
|
|
|
Теперь известно ускорение точки А. Ее принимаем за полюс при расчетах ускорений точек В и С. Причем вначале будем выполнять расчет для точки В, так как известна траектория ее движения.
Ускорения точек А и В связаны зависимостью
.
Точка В движется по прямой, поэтому у нее отсутствует нормальное ускорение, а ее полное ускорение 
равно касательному 
, которое лежит на прямой ОВ, как это показано на рисунке 3.14.
Тогда с учетом выражения (3.6) приходим к векторному равенству
. (3.7)
Вектор направляется перпендикулярно отрезку АВ в сторону углового ускорения звена 2 (оно выбирается произвольно), а вектор – от точки В к точке А. Значение нормального ускорения
см/с2.
Для определения углового ускорения звена АВ и полного ускорения точки В используем метод проецирования.
Замечание: расстояние от полюса А до МЦС звена АВ с течением времени изменяется. Поэтому применение дифференцирования выражения угловой скорости для определения углового ускорения звена АВ приведет к весьма громоздким выкладкам.
Проецируя выражение (3.7) на оси координат, получаем
Оx: 
; (3.8)
Оy: 
. (3.9)
Из уравнения (3.9) определяем 
Из уравнения (3.8) находим 
.
Знак «минус», получившийся при расчете ускорения точки B, показывает, что его действительное направление противоположно изображенному на рисунке 3.14.
Поскольку касательное ускорение в движении точки В вокруг А выражается через угловое ускорение формулой , то
.
Теперь находим ускорение точки С. В качестве полюса снова используем точку А. Тогда ускорение точки С
. (3.10)
Уже найдено угловое ускорение 
. Поэтому сейчас можем рассчитать и касательное, и нормальное ускорения в движении С вокруг А:
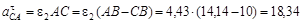см/с2;
см/с2.
Векторы , направляются аналогично векторам и .
Траектория точки С неизвестна, поэтому удобнее искать проекции ее ускорения на оси декартовой системы координат, проецируя выражение (3.10) на эти оси:
,
.
Тогда полное ускорение точки С
см/с2.
Условие задания К-3
Определение скоростей и ускорений при плоском движении тел
|
|
|
На рисунке 3.15 приведены расчетные схемы механизмов, а также исходные данные для выполнения задания. На их основании:
1 Изобразить в масштабе схему механизма и показать на нем векторы скоростей точек В и С со всеми необходимыми построениями и указать направления вращения звеньев, движущихся непоступательно.
2 По заданной схеме и исходным данным рассчитать линейные скорости точек В и С и угловые скорости звеньев механизма.
3 Определить линейные ускорения точек В и С и угловые ускорения звеньев; изобразить на схеме все составляющие линейных ускорений точек и угловые ускорения звеньев механизма.
   ; 
| 
   
| ||||
| 
     
| ||||
 
  | 
 
 
|
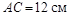
Рисунок 3.15
| 
 
 
| ||||
| 
  
| ||||
| 
 
|
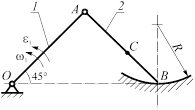
Рисунок 3.15 (продолжение)
| 
 
 
| ||||
| 
    
| ||||
| 
   
|
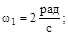
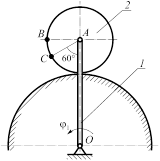
Рисунок 3.15 (продолжение)
| 
 
 
| ||||
  
| 
 
| ||||
| 
 
|
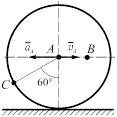
Рисунок 3.15 (продолжение)
| 
 
| ||||
| 
 
| ||||
| 
 
|
Рисунок 3.15 (окончание)
|
|
|
