 |
Определение всех токов в цепи методом узловых потенциалов.
|
|
|
|
Задание на курсовую работу
По дисциплине «Теория электрических цепей»
Часть 1. Линейные электрические цепи однофазного синусоидального тока
Принципиальная схема электрической цепи изображена на рисунке 1. Параметры элементов цепи выбираются по вариантам, приведенным в таблице П.1. Схема состоит из шести ветвей, поэтому в ней шесть токов. Количество узлов схемы 4. Во всех ветвях схемы изображены источник ЭДС Е и комплексное сопротивление Z. В зависимости от номера ветви и варианта ветвь может содержать только активное сопротивление R (в ветви только резистор), только реактивное сопротивление L, С, или LС (в ветви будет изображены или только конденсатор, или только катушка индуктивности, или последовательно соединенные конденсатор и катушка), или комплексное сопротивление R+j*XL или R-j*XС (изображаются последовательным соединением резистора с катушкой индуктивности или конденсатором соответственно). Источники ЭДС в каждом из вариантов находятся лишь в трёх ветвях. Для каждого из вариантов заданы номера этих ветвей, амплитудные значения напряжений и начальные фазы этих источников. В остальных трёх ветвях источники энергии отсутствуют.
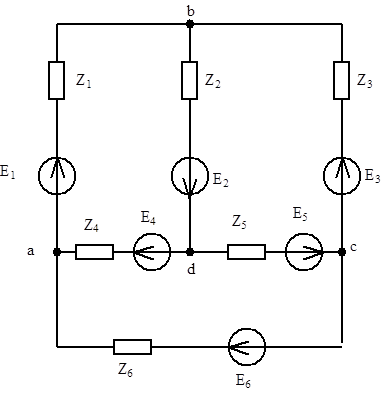
Рисунок 1. Заданная схема цепи к первой части курсовой работы.
Последовательность выполнения
первой части курсовой работы:
Составление расчетной схемы электрической схемы.
1.1. Составляется принципиальная схема электрической цепи для своего варианта задания, т.е. изображаются только заданные источники, а каждое комплексное сопротивление представляется последовательным соединением резистора, и/или конденсатора, и/или катушки индуктивности. Номера всех элементов на схеме рекомендуется задать согласно нумерации ветвей в исходной схеме (рис. 1). Для определенности назовем схему ERCL – схемой.
|
|
|
1.2. На принципиальной схеме выбираются произвольно направления токов в ветвях и направления обхода независимых контуров. Рекомендуется выбирать направления токов сонаправленными ЭДС в этих ветвях (направления ЭДС указаны на рис. 1). Рекомендуется выбирать короткие (внутренние) независимые контуры, а направление их обхода выбрать по часовой стрелке.
1.3. Представить заданные в схеме источники в символической (комплексной) форме. Здесь и далее все комплексные значения должны быть представлены в алгебраической и показательной формах. Основной для токов и напряжений является показательная форма, для сопротивлений и проводимостей – алгебраическая.
1.4. Рассчитать в численном виде значение всех сопротивлений (активных, индуктивных и ёмкостных) полученной цепи.
1.5. Заменить последовательно-соединенные элементы в ветвях их комплексными сопротивлениями. Представить эквивалентную схему цепи, в которой в каждой ветви находится не более одного источника и не более одного комплексного сопротивления (по аналогии с рис. 1). Подпишите на схеме численные значения всех элементов. Для определённости назовем эту схему EZ-схемой.
Определение всех токов в цепи с помощью законом Кирхгофа.
2.1. Записать систему уравнений, составленных по законам Кирхгофа, в дифференциально-интегральной форме (по ERCL-схеме). Подставлять численные значения ЭДС и пассивных элементов в систему не требуется.
2.2. Записать систему уравнений, составленных по законам Кирхгофа, в символической (комплексной) форме
- в общем виде («в буквах») по ERCL-схеме;
- в общем виде(«в буквах») по EZ-схеме;
- с подставленными численными значениями E и Z (по EZ-схеме).
2.3. Найти токи во всех ветвях, решив систему уравнений вручную или с помощью математических пакетов программ.
|
|
|
Определение токов в цепи с помощью метода контурных токов
3.1. Составить систему уравнений по методу контурных токов (по EZ-схеме), в общем виде
3.2. Привести формулы и расчет коэффициентов системы и столбца свободных членов.
3.3. Записать систему уравнений с подставленными значениями коэффициентов.
3.4. Найти контурные токи, решив систему линейных уравнений вручную или с помощью математических пакетов программ.
3.5. Привести формулы и расчет токов во всех ветвях цепи по найденным контурным токам.
Определение всех токов в цепи методом узловых потенциалов.
4.1. Составить систему уравнений по методу узловых потенциалов (по EZ-схеме), в общем виде. В качестве общей точки (узла с нулевым потенциалом, «земли») рекомендуется использовать узел с (рис. 1).
4.2. Привести формулы и расчет коэффициентов системы и столбца свободных членов.
4.3. Записать систему уравнений по методу узловых потенциалов с подставленными значениями коэффициентов.
4.4. Найти потенциалы в узлах схемы, решив систему линейных уравнений вручную или с помощью математических пакетов программ.
4.5. Привести формулы и расчет токов во всех ветвях цепи по найденным узловым потенциалам.
5. Расчет тока I3 методом эквивалентного генератора.
5.1. Представить эквивалентную схему замещения электрической цепи, состоящую из эквивалентного генератора и сопротивления z3.
5.2. Представить аналитическое выражение и расчет ЭДС эквивалентного генератора.
5.3. Представить аналитическое выражение и расчет внутреннего сопротивления эквивалентного генератора.
5.4. Представить аналитическое выражение и расчет тока I3 с помощью теоремы об эквивалентном генераторе.
6. Определение показаний ваттметра и варметра в ветви цепи. Проверка балансов мощности.
6.1. Изобразить принципиальную схему электрический цепи, предусмотрев в ней измерительные приборы для измерения протекающей активной и реактивной мощностей, рассеиваемой в ветви №3. Генераторные зажимы ваттметра и варметра подключаются в начало ветви – узел b.
6.2. Выполнить расчет показаний амперметра и ваттметра двумя способами:
- 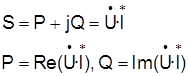 (1)
(1)
- 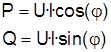 (2)
(2)
Обеспечить сходимость результатов расчета, полученных разными методами. При необходимости откорректируйте расчет, сделайте вывод, какую смысловую нагрузку несет знак полученного результата
|
|
|
6.3. Привести формулу и расчет полной мощности, генерируемой всеми источниками в цепи;
6.4. Привести формулу и расчет полной мощности, потребляемой всеми сопротивлениями в цепи (по ERCL-схеме). Обеспечить сходимость баланса мощности с точностью ± 0.1Вт и ±0.1ВА.
7. Построение потенциальной диаграммы схемы, совмещенной с векторной диаграммой токов.
7.1. Обозначить на ERLC – схеме исследуемой цепи контрольные точки, являющиеся местами соединения смежных элементов схемы (например, между источником и резистором в ветви, между резистором и конденсатором). Контрольные точки обозначаются строчными буквами латинского алфавита, не использованными при обозначении узлов цепи. Принять за общую точку (с нулевым потенциалом) узел с.
7.2. C помощью закона Ома для участка цепи последовательно рассчитать значения потенциалов во всех контрольных точках. Целесообразно рассчитывать потенциалы контрольных точек последовательно по ветвям. Сначала рассчитываются потенциалы контрольных точек в ветвях, начинающихся либо заканчивающихся в узле с – общей точке. При этом потенциалы вторых концов ветвей – потенциалы узлов a, b, d должны совпасть с узловыми потенциалами, рассчитанными в п.4.4 (если «заземленным» был один и тот же узел).
7.3. На комплексной плоскости (рисунок формата А4). Изобразить векторную диаграмму токов в цепи. Изобразить векторы токов направленными отрезками, исходящими из начала координат. Масштаб токов выбирается заранее и должен быть одинаков по обеим осям диаграммы, для реалистичного отображения углов.
7.4. На комплексную плоскость с построенной векторной диаграммой токов нанести точки, отображающие потенциалы всех узлов и контрольных точек, рассчитанные в п. 7.2. Точки должны быть подписаны. Масштаб напряжений потенциальной диаграммы может численно отличаться от масштаба токов векторной диаграммы (так как значения токов, как правило, на порядок меньше), но также должен быть одинаков по обеим осям. Точки на диаграмме соединяют между собой векторами в соответствии с ERLC- схемой: каждый вектор (ребро графа) будет обозначать напряжение на каком-либо элементе схемы (резисторе, конденсаторе, катушке индуктивности или источнике). Следует подписать эти напряжения (буквами).
|
|
|
7.3. Численные значения токов и потенциалов в показательной форме следует нанести на полученную совмещенную векторную диаграмму токов и потенциальную диаграмму напряжений, чтобы они не закрывали элементы этой диаграммы: узлы, векторы, оси. При необходимости можно использовать выноски. В свободном углу диаграммы наносятся значения масштабов по току и напряжению.
8. Составление системы уравнений по законам Кирхгофа для цепи с магнитными связями.
8.1. Полагая, что между любыми двумя катушками индуктивности, включенными в цепь (ERLC – схема), имеется индуктивная связь, составить два варианта принципиальной электрической схемы цепи – для встречного и согласного включения катушек индуктивности (соответственно схемы В (встречное) и С (согласное) схемы). Фактически требуется в схеме, полученной в п. 1.1, обозначить одноименные выводы выбранных катушек в соответствии со способом их включения (встречное или согласное) и выбранными в п.1.2 направлениями токов в ветвях.
8.2. Записать два варианта (для схемы В и схемы С) системы уравнений, составленных по законам Кирхгофа в дифференциально-интегральной форме, с учетом индуктивной связи. Подставлять численные значения ЭДС и пассивных элементов в эти системы не требуется.
8.3. Записать два варианта системы уравнений (для схемы В и схемы С), составленных по законам Кирхгофа в символической (комплексной) форме с учетом магнитных связей. Подставлять численные значения ЭДС и пассивных элементов в эти системы не требуется.
Численные результаты работы целесообразно свести в таблицу, в которой в заголовках строк разместить исходные и искомые величины (ЭДС источников, комплексные сопротивления ветвей, токи в ветвях, напряжения в узлах и контрольных точках, активные и реактивные мощности в элементах схемы), в заголовках столбцов – методы, используемые в работе (ЗК- законы Кирхгофа, МКТ – метод контурных токов, МУП – метод узловых потенциалов, БМ – баланс мощностей, ПД – потенциальная диаграмма). В ячейки таблицы в двух формах – алгебраической и показательной должны быть записаны значения этих величин. Не все ячейки таблицы будут заполнены, так как не все величины были рассчитаны каждым из предложенных методов.
|
|
|


