Главная | Обратная связь | Поможем написать вашу работу!

Методика расчета параллельно– последовательной резистивной цепи

Пусть дана цепь с параллельно– последовательным соединением резисторов (рис. 2.6, а). Известны значение ЭДС источника , величины сопротивлений , , , .

Рис. 2.6. Параллельно– последовательное соединение резисторов

Определить силу тока во всех ветвях схемы — , , и напряжения на каждом резисторе — , , , .

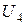Решение:

1. В соответствии со свойством последовательного соединения элементов, определим 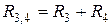. Схема примет вид, показанный на рис. 2.6, б.

2. В соответствии со свойством параллельного соединения элементов, определим . Схема примет вид, показанный на рис. 2.6, в.

3. Рассчитываем эквивалентное сопротивление цепи: (рис. 2.6, г).

4. По закону Ома рассчитываем ток .

5. Ток протекает через последовательно соединенные резисторы и , следовательно, можно найти падения напряжения на резисторах и (рис. 2.6, в): , .

По второму закону Кирхгофа делаем проверку .

6. Напряжение приложено к параллельно соединенным резисторам и (рис. 2.6, б). Следовательно, можно найти токи, протекающие через резисторы и : , . По первому закону Кирхгофа делаем проверку: .

7. Ток 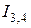протекает через резисторы и , следовательно, можно найти падения напряжения на резисторах и : , . По второму закону Кирхгофа делаем проверку .

Таким образом, методика расчета простой электрической цепи сводится к двум этапам.

На первом этапе схема последовательно сводится к элементарному виду с одним источником и одним резистором (рис. 2.6, г). В элементарной схеме определяются ток или напряжение.

На втором этапе схема последовательно наращивается от простейшей к исходной, с определением искомых токов и напряжений.

Метод контурных токов.

Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом законов Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурные токи, замыкающиеся в контурах. На рис. 3.1 в виде примера показана двухконтурная цепь, в которой I₁₁ и I₂₂ - контурные токи. Токи в сопротивлениях r₁ и r₂ равны соответствующим контурным токам; ток в сопротивлении r₃ являющемся общим для обоих контуров, равен разности контурных токов I₁₁ и I₂₂, так как эти токи направлены в ветви r₃ встречно.

Рис. 3.1. К расчету методом контурных токов

Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, то есть для электрической схемы с числом узлов q и числом ветвей p задача нахождения контурных токов сведется к решению системы p-q +1 уравнений. Так, в схеме рис. 3.1 q = 2 p = 3; следовательно, число уравнений равно 3-2+1=2 (число уравнений независимых контуров).

Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от заданного контурного тока в сопротивлениях, входящих в контур, берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 3.1, где направление обоих контурных токов выбрано по ходу часовой стрелки.

Для заданной электрической схемы с двумя независимыми контурами ( рис. 3.1 ) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:

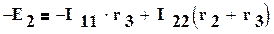здесь (r₁ + r₃) и (r₂ + r₃) - собственные сопротивления контуров 1 и 2, r₃ - общее сопротивление контуров 1 и 2. После определения контурных токов, легко найти и токи всех ветвей.