 |
Давления на стенки бункера
|
|
|
|
На стенки бункера, заполненного материалом, действуют давления от массы материала, которые зависят от физико-механических свойств материала (плотности, влажности, сыпучести), а также от коэффициента трения материала о стенки, способа формирования материала в бункере, формы бункера и др.
Давление на дно бункера
Если материал по своим физико-механическим свойствам близок к жидкости, то вертикальное давление Ру (Па), действующее на дно бункера, близко к гидравлическому
Ру =  ,
,
где h – глубина расположения рассматриваемой точки над уровнем материала, м;
 – плотность материала, кг/м3;
– плотность материала, кг/м3;
q – ускорение силы тяжести, м/с2.
Для материалов хорошо сыпучих в результате действия сил внутреннего трения, а также сил трения материала о стенки бункера давление на дно уменьшается. Это влияние учитывает коэффициент зависания Кз. Тогда
Ру =  . Кз.
. Кз.
Коэффициент Кз тем выше, чем большее значение имеет коэффициент бокового распора 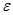 , который равен
, который равен  Рх / Ру, где Рх – боковое давление в рассматриваемой точке. Так для жидкости
Рх / Ру, где Рх – боковое давление в рассматриваемой точке. Так для жидкости  и Кз = 1. Для хорошо сыпучих материалов
и Кз = 1. Для хорошо сыпучих материалов  , тогда Кз можно принимать в пределах в пределах 0,8–0,9. Точное определение Кз находят по зависимости
, тогда Кз можно принимать в пределах в пределах 0,8–0,9. Точное определение Кз находят по зависимости
К3 =  ,где x =
,где x =  ;
;
f – коэффициент трения материала о стенки бункера;
R0 – гидравлический радиус (отношение площади дна бункера к периметру), м.
При загрузке бункера с большой высоты или возможности образования внутри бункера пустот и затем резкого падения материала давление на дно бункера значительно увеличивается. Это явление учитывает коэффициент динамики Кq. Для бункеров, оборудованных вибраторами, Кq = 1,3  1,5; при загрузке бункера с большой высоты Кq = 1,1
1,5; при загрузке бункера с большой высоты Кq = 1,1  1,4; при зависании материала с образованием пустот Кq = 2.
1,4; при зависании материала с образованием пустот Кq = 2.
|
|
|
Давление на дно бункера с учетом всех вышеизложенных факторов
Ру =  . Кз . Кq.
. Кз . Кq.
Давление на вертикальные стенки бункер
Давление на вертикальные стенки Рx определяется
Рx = Ру .  . Кз . Кq.
. Кз . Кq. 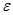 ,
,
где 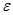 – коэффициент бокового давления, зависящий от свойств материала и может быть определен экспериментально или по зависимости
– коэффициент бокового давления, зависящий от свойств материала и может быть определен экспериментально или по зависимости  (
( – угол естественного откоса материала).
– угол естественного откоса материала).
Давление на наклонные стенки бункера
Для определения давлений на наклонные стенки бункера пользуются теорией сыпучих тел, согласно которой давление в произвольной точке массы следует закону эллипса напряжений, главными полуосями которого является вертикальное давление Ру и горизонтальное Рx. Основываясь на этом полное давление Рп, нормальное Рн и тангенциальное 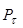 можно определить графическим путем (рис. 2.3).
можно определить графическим путем (рис. 2.3).

Рис. 2.3. Схема давлений на наклонную стенку бункера
Возьмем на наклонной стенке бункера точку О, лежащую на кромке выпускного отверстия и определим величину полного давления считая, что бункер заполнен материалом по кромку СD. Приняв точку О за центр, построим на ней эллипс напряжений с модулями осей ОВ = Рx и ОА = РУ. Из точки О проведем перпендикулярно ОD нормаль n и радиусом равным длине ОВ засекаем на n точку Е, а радиусом ОА точку И. Из точек Е и И проводим линии параллельные полуосям до их пересечения в точке К, которая будет лежать на эллипсе напряжений. Отрезок КО представляет собой вектор полного давления в точке О (Рп = КО).
Нормальное и касательное давление Рн = КЛ и 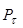 = ОЛ. Во всех остальных точках стенки О полное и нормальное давления имеют то же направление, что и в точке О и изменяются по закону прямой линии DM.
= ОЛ. Во всех остальных точках стенки О полное и нормальное давления имеют то же направление, что и в точке О и изменяются по закону прямой линии DM.
Кроме того, полное давление на стену бункера в точке О можно определить аналитически, зная угол наклона стенки бункера
Pп  Па,
Па,
а нормальные и касательные составляющие
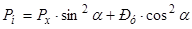 Па,
Па,
 Па,
Па,
где  – угол наклона стенки к горизонту.
– угол наклона стенки к горизонту.
|
|
|
Шиберные затворы
Шиберные затворы имеют вид плоской задвижки, перемещающиеся в пазах, расположенных по сторонам прямоугольного выпускного отверстия. Приводятся в действие ручным рычажным одно- или двух- реечным механизмом с помощью механического привода или гидропневмоцилиндров. Затворы этого типа применяются для бункеров, работающих на хорошо сыпучих материалах.
Схема затвора с механическим приводом представлена на рис. 3.1. Для затворов больших размеров и воспринимающих большие нагрузки вместо направляющих скольжения применяют роликовые опоры.
Расчет шиберных затворов сводится к определению усилия, необходимого для открытия шибера затвора, которое наибольшее в начальный момент трогания с места.
При открывании затвора по направляющим скольжения действуют следующие силы сопротивления (рис. 3.2).
Усилие открывания определяется
Р = (Р 1 + Р 2) . К 3.
Учитывая, что Р 1 = Ру . а . в . f 1 и Р 2 = (Ру . а . в + m ш . q). f 2, получим
Р = [ Ру . а . в . f 1 + (Ру. а . в + mш . q) . f 2] . K 3,
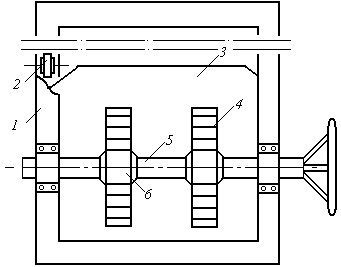
Рис. 3.1. Схема шиберного затвора
1 – металлоконструкция; 2 – опорный ролик; 3 – шибер;
4 – рейка; 5 – вал; 6 - зубчатое колесо

Рис. 3.2. Схема действия сил на шибер
Р 1 – сила сопротивления от трения материала по шиберу;
Р 2 – сила сопротивления в направляющих шибера
где mш – масса шибера, кг;
f 1 и f 2 – коэффициенты трения материала по шиберу и шибера по направляющим;
q – ускорение силы тяжести;
Ру – вертикальное давление, действующее на затвор, Па;
К 3 – коэффициент запаса, учитывающий возможность перекоса и заедания затвора, К 3 = 1,25-1,5.
При движении шибера по направляющим качения усилие открывания (рис. 3.3.)
Р = (Р 1 + Р 3 + Р 4 .  ) . К 3,
) . К 3,
где Р 3 – сопротивление качению шибера по ролику,
Р 3 = Р . а . в . К,
где К = 0,01–0,012 – коэффициент сопротивления качению стали по стали;
Р 4 – сопротивление трения в оси ролика, которое определяется
Р 4 = (Ру . а . в + mш . q) . f 3,
где f 3 – коэффициент трения в оси ролика;
d – диаметр оси, м;
D – диаметр ролика, м.
Скорость открывания затвора
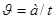 ,
,
где t – время перемещения затвора в крайнее положение, с.
Мощность, затрачиваемая на перемещение затвора
 Вт
Вт

Рис. 3.3. Схема действия сил на ролик
|
|
|
Секторные затворы
 Секторные затворы делятся на односекторные и двухсекторные (челюстные). Простой секторный затвор (рис. 3.4, а) представляет собой сектор 1, вращающийся на пальцах, закрепленных на боковых стенках корпуса 2, который имеет квадратное сечение и крепится к отверстию бункера. Управляется с помощью гидравлических или пневматических цилиндров 3, а также механической передачей. Такие затворы применяются преимущественно в бункерах для хорошо сыпучих материалов с мелкими и средними кусками.
Секторные затворы делятся на односекторные и двухсекторные (челюстные). Простой секторный затвор (рис. 3.4, а) представляет собой сектор 1, вращающийся на пальцах, закрепленных на боковых стенках корпуса 2, который имеет квадратное сечение и крепится к отверстию бункера. Управляется с помощью гидравлических или пневматических цилиндров 3, а также механической передачей. Такие затворы применяются преимущественно в бункерах для хорошо сыпучих материалов с мелкими и средними кусками.
Челюстной затвор состоит из двух секторов или челюстей 1 (рис. 3.4, б), которые соединены между собой зубчатыми секторами 2, находящимися в зацеплении. Обе челюсти открываются и закрываются одновременно. Челюстные затворы лучше приспособлены для частых открываний и закрываний бункеров и регулирования подачи материала.
При расчете секторного или челюстного затвора учитывается, что наибольший момент необходимо приложить в начале открывания затвора. Суммарный момент сопротивления складывается из потерь на трение в цапфах или подвесках М 1 и от трения материала о сектор М 2.

Рис. 3.4. Схема затворов: а – секторный, б – челюстной
М = М 1 + М 2.
Момент М 1 = F 1 . 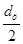 = (Ру . а . в + m c . q) . f ц .
= (Ру . а . в + m c . q) . f ц .  Н.м,
Н.м,
где F 1 – сила трения в цапфе, Н;
Р у – давление, действующее на затвор, Па;
mc – масса сектора, кг;
fц – коэффициент трения в цапфе;
dц – диаметр цапфы, м;
а и в – размеры выпускного отверстия, м.
Момент
М 2 = F 2 . R = Ру . а .в . f 1 . R,
где F 2 – сила трения материала о сектор, Н;
f 1 – коэффициент трения материала о сектор;
R – радиус вращения сектора, м.
Усилие, необходимое для открывания секторного затвора
Р = М / R Н.
Лотковые затворы
Применяются для различных по крупности материалов, из-за чего они нашли широкое применение. Рабочим органом лоткового затвора является шарнирно закрепленный под выпускным отверстием лоток (рис. 3.6). При закрытом положении затвора лоток 1 находится в горизонтальном положении. При перемещении лотка относительно шарнира О на угол больший угла естественного откоса материала, последний скользит по дну лотка и удаляется из бункера. Кроме этого с увеличением угла наклона лотка соответственно увеличивается скорость движения материала и его производительность. Подъем и опускание лотка осуществляется с помощью пневмо или гидроцилиндра, связанных с проушиной 2. Для уменьшения нагрузок на привод в затворе имеется противовес 3.
|
|
|
Расчет затвора сводится к определению усилия Р, необходимого для подъема лотка с находящимся на нем материалом.

Рис. 3.6. Схема лоткового затвора
Для расчета затвора принимаем следующие обозначения:
В – сторона квадрата выпускного отверстия, м;
В 1 – ширина лотка, м;
L – длина лотка, м;
hср – средняя высота загрузки лотка, м;
 – плотность материала, кг/м3;
– плотность материала, кг/м3;
q – сила тяжести одного погонного метра лотка, Н;
Q – сила тяжести сыпучего материала на лотке, Н;
G 0 – сила тяжести контр груза, Н;
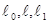 – плечи сил, м.
– плечи сил, м.
Рассматривая действие сил относительно оси поворота О получим
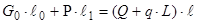 Н. м. (3.1)
Н. м. (3.1)
Среднюю высоту загрузки лотка по его длине можно с запасом считать hср = 0,4 . В 1, следовательно, сила
Q = B 1 . L . 0,4 . В 1 .  = 0,4 . В 12. L.
= 0,4 . В 12. L.  Н. (3.2)
Н. (3.2)
Принимая  ≈ 0,5 L и коэффициент запаса К = 1,3 получим из (3.1)
≈ 0,5 L и коэффициент запаса К = 1,3 получим из (3.1)
Р =  Н.
Н.
|
|
|


