 |
Определение оценок параметров закона распределения результатов измерений или случайных погрешностей измерений.
|
|
|
|
Определение точечных оценок параметров законов
Распределения результатов измерений
Цель работы: изучить точечные характеристики распределений результатов измерений и освоить методику их оценки и расчетов.
Приборы и принадлежности: дозиметр-радиометр АНРИ-01 “СОСНА”.
Краткие теоретические сведения
Порядок обработки результатов наблюдений при многократных измерениях состоит из ряда последовательно выполняемых этапов:
1. Определение точечных оценок параметров законов распределения результатов измерений. На этом этапе после ранжирования значений выборки (X)в порядке возрастания и представления ее в виде вариационного ряда (х1 ≤ х2 ≤ … ≤ хn) определяются:
· оценка центра распределения (Xц р);
· оценка среднеквадратического отклонения СКО отдельных результатов наблюдений (S);
· оценка СКО среднего арифметического значения (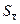
).
В соответствии с критериями исключаются грубые погрешности (промахи) и вводятся поправки на систематические погрешности. После их исключения проводится повторный расчет оценок среднего арифметического значения и оценок СКО наблюдений и измерений.
Определение оценок параметров закона распределения результатов измерений или случайных погрешностей измерений.
В этом случае от выборки результатов измерений x 1, x2,..., xn переходят к выборке отклонений от среднего арифметического Δ x 1, Δ x 2, …, Δ x n
(1)
Для оценки параметров закона распределения проводится построение по исправленным результатам измерений xi, где i = 1,2, …, n, - члены вариационного ряда (упорядоченной выборки) yi, где y1 = min(xi) и yn = max(xi). По виду статистических функций распределений (представленных в виде гистограмм или полигонов - для дифференциальной формы или в виде кумулятивной кривой - для интегральной формы) может быть оценен закон распределения результатов наблюдений;
|
|
|
3. Оценка закона распределения по статистическим критериям согласия. Для проверки гипотез о виде функции распределения экспериментальных данных используют следующие критерии согласия: Пирсона, Мизеса-Смирнова, составной критерий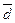 
. При числе наблюдений n >50 для идентификации закона распределения используется критерий Пирсона (хи-квадрат) или критерий Мизеса-Смирнова (ω2). При 15 < n < 50 для проверки нормальности закона распределения применяется составной критерий (d -критерий), приведенный в ГОСТ 8.207-76. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется. При этом нахождение доверительных границ случайной погрешности результата измерения по методике, предусмотренной ГОСТ 8.207-76 и описываемый далее, возможна в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению. В случае если гипотеза о принадлежности полученных результатов к нормальному закону распределения не подтверждается, то проводится приближенная оценка параметров законов распределения (идентификацией формы и вида закона распределения соответствующему теоретическому).
4. Определение доверительных интервалов случайной погрешности. Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находят квантильный множитель zp при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности
Δ= ±zp .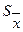 
.
5. Определение границ не исключенной систематической погрешности результата измерений. Под этими границами понимают найденные нестатистическими методами границы интервала, внутри которого находится неисключенная систематическая погрешность. Она образуется из ряда составляющих, как правило, погрешностей метода и средств измерений, а также субъективной погрешности;
|
|
|
6. Определение доверительной границы погрешности результата измерения Δ p. Данная операция осуществляется путем суммирования СКО случайной составляющей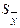 
и границ неисключенной систематической составляющей Ө в зависимости от соотношения этих погрешностей между собой;
7. Формирование результата измерений.
|
|
|
