 |
Определение оценок среднеквадратического отклонения
|
|
|
|
Оценка S 2 генеральной дисперсии σ2 любого закона распределения может быть вычислена (при неизвестном математическом ожидании генерального среднего) по формуле:
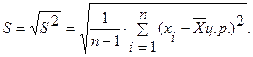 (17)
(17)
Эта оценка является несмещенной и состоятельной, а для нормального распределения - еще и эффективной.
Для нормального закона распределения оценка генерального среднеквадратического отклонения (СКО) S результатов наблюдений определяется:
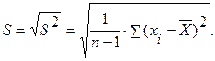 (18)
(18)
Оценка является несмещенной, состоятельной и асимптотически эффективной только для нормального закона. В случае представления результатов вариационным рядом следует пользоваться формулой (5.3).
Несмещенная оценка СКО для нормальных распределений так же определяется по формуле:
 (19)
(19)
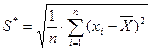 (20)
(20)
Значения коэффициента М к приведены в таблице 1
Таблица 1 - Значения коэффициента М к в зависимости от количества наблюдений п
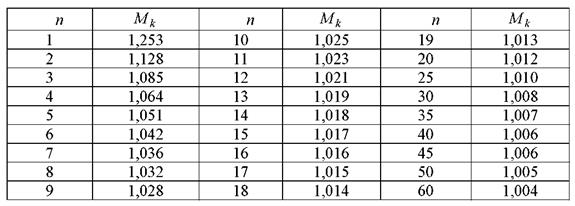
СКО случайной погрешности оценки центра распределения (СКО результата измерений) убывает по сравнению с СКО результата наблюдений
в  как показано по формуле:
как показано по формуле:
 (21)
(21)
Определение оценок третьего центрального момента μ 3 коэффициента асимметрии γa, СКО коэффициента асимметрии σ (уa) проводится по формулам:
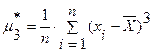 ; (22)
; (22)
 (23)
(23)
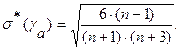 (24)
(24)
Формулы для вычисления начальных ak и центральных μ k моментов и соотношения между ними приведены в таблице 2.
Таблица 2 - Перечень формул

Выбор формул, приведенных во второй и третьей графах таблицы и дающих практически одинаковые результаты, осуществляют в зависимости от особенностей используемых средств вычислительной техники, алгоритмов и программ обработки информации.
Рассмотрим на примере последовательность определения оценок центра распределения. Даны результаты 20 измерений перемещения для точек пера лопатки компрессора под действием центробежной силы. Результаты наблюдения и частота их появления указаны в таблице 3.
|
|
|
Таблица 3 - Результаты наблюдений

Требуется определить оценки результата измерения и СКО результатов наблюдений и измерения.
Будем считать, что закон распределения не известен. В этом случае, как отмечалось раньше, за оценку центра распределения экспериментальных данных принимают медиану из ряда пяти оценок центров  (расположенных в вариационный ряд).
(расположенных в вариационный ряд).
Определяем оценку центра как:
· среднее арифметическое по формуле (4):
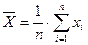
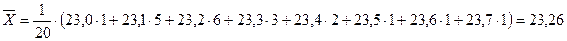 мкм;
мкм;
среднее арифметическое 90 %-ной выборки определяем по
формуле (7). Пять процентов выборки в нашем случае 0,05 . n = 0,05 . 20 =1,
т. е. один результат измерения. Отбрасываем по одному измерению с концов
вариационного ряда, т. е. результаты x1 = 23,0 мкм и x20 = 23,7 мкм.
Тогда:
 мкм;
мкм;
· медиану распределения - по формуле (9). Поскольку n -четное, то
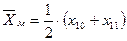 мкм
мкм
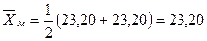 мкм;
мкм;
· срединный размах определяем по формуле (15). Для этого вычисляем 25 % и 75 %-ные квантили опытного распределения. Этими квантилями являются точки между 4 и 5, а также между 16 и 17 результатами:
 мкм;
мкм; 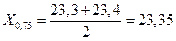 мкм.
мкм.
Тогда:
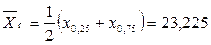 мкм.
мкм.
· центр размаха определяем по формуле (16):
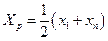 мкм
мкм
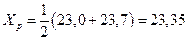 мкм.
мкм.
Полученные оценки центра распределения располагаем в вариационный ряд:
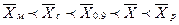 или
или
23,20 < 23,225 < 23,25 < 23,26 < 23,35 мкм.
За оценку центра распределения (результата измерения) окончательно принимаем среднее арифметическое 90 %-ной выборки, так как эта оценка занимает медианное положение в ряду оценок: 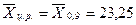 мкм.
мкм.
Оценку СКО результатов наблюдений вычисляем по формуле (17):
 мкм.
мкм.
Оценку СКО результатов измерений определяем по формуле (21):
 мкм.
мкм.
ПОРЯДОК выполнения работы
1 Изучить устройство и принцип работы дозиметра-радиометра АНРИ-01 “СОСНА”.
|
|
|
2 Получить допуск к проведению измерений.
3 Провести измерения удельной активности гамма-излучения в лаборатории (не менее 30 измерений).
4 Выполнить обработку результатов измерений по методике описанной в теоретической части работы.
5 Результаты измерений и результаты расчетов занести в таблицу
| Хi | 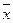
| 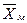
| 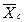
| 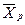
| 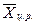
| 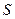
| 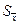
|
| … | |||||||
6 Сделать выводы.
Контрольные вопросы:
1. Дать определение точечной оценки.
2. Какую оценку называют несмещенной? эффективной? состоятельной?
3. Как определяется выборочное среднее?
4. Как определить несмещенную и состоятельную оценку математического ожидания генеральной совокупности?
5. Дать определение выборочной дисперсии. Каким свойством оценок она обладает?
6. Как определяются мода и медиана совокупности?
7. Понятие интервальной оценки неизвестного параметра генеральной совокупности.
8. Как найти интервальную оценку для генеральной средней нормально распределенной совокупности при известном среднем квадратическом отклонении?
9. Как найти интервальную оценку для генеральной средней нормально распределенной совокупности при неизвестном среднем квадратическом отклонении?
10. Каким образом определяется интервальная оценка среднего квадратического и дисперсии нормально распределенной генеральной совокупности?
Литература:
1 Сытько В.В. Теоретическая метрология. 1. Физические величины и их
измерение. Мн., - 1998.
2 Сергеев А.Г., Крохин В.В. Метрология: Учебное пособие для вузов. - М.:
Логос, 2001.
3 Маркин Н.С. Введение в метрологию. - М.: Издательство стандартов, 1991.
4 Тойберг П. Оценка точности результатов измерений. - М.: Энергоатомиздат,
1988.
5 Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений.
- М.: Энергоатомиздат, 1990.
|
|
|


