 |
Расчет зубьев прямозубой конической передачи на изгиб
|
|
|
|
3.74. Расчет производят по аналогии с расчетом цилиндрической прямозубой передачи (см. шаги 3.33—3.38).
Опытным путем установлено, что нагрузочная способность конической передачи ниже, чем цилиндрической. В соответствии с этим в расчетные формулы для зубьев конической передачи вводят коэффициент КFO, учитывающий снижение их нагрузочной способности по сравнению с зубьями цилиндрических передач.
Расчет на прочность зубьев при изгибе производят по среднему значению модуля зубьев т. Коэффициент формы зуба YF выбирают по аналогии с цилиндрической прямозубой передачей, но в зависимости от числа зубьев эквивалентных колес zV = z/cosδ.
Под числом зубьев z3 эквивалентных колес понимают такое число зубьев, которое может расположиться на длине окружности (см. рис. 3.47) радиусом, равным длине образующей дополнительного конуса О1А.
По какому модулю производят расчет геометрических параметров и по какому модулю — расчет на прочность конической передачи?
3.75. Проверочный расчет следует проводить по аналогии с прямозубой передачей.
Расчетные напряжения изгиба в зубьях конических колес и условие прочности выражаются формулой
(3.28)
где σF — возникающее напряжение изгиба, МПа; Т2 — вращающий момент на колесе, Н • мм; КFβ, KFu — коэффициенты нагрузки (см. табл. 3.4, 3.5); Ψbd — коэффициент длины зуба (см. шаг 3.71); YF — коэффициент формы зуба (выбирают по табл. 3.6) в зависимости от zV; z1 — число зубьев шестерни; и — передаточное число; m = me-(b/z)sinδ — средний модуль, мм; КFθ = 0,85 — опытный коэффициент снижения нагрузочной способности; [σ]F — допускаемое напряжение изгиба, МПа (см. шаг 3.39).
Для z2 = 72, δ2 = 75°58/ выберите из табл. 3.6 коэффициент формы зуба и концентрации напряжений.
|
|
|
3.76. Проектировочный расчет. Средний модуль зубьев определяется по формуле
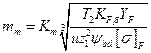(3.29)
где т, мм; Т2, Н • мм; [a]F, МПа; Кт= 1,45 — вспомогательный коэффициент для стальных прямозубых конических колес; Ψbd = b/dt принимают Ψbd =0,3 ÷ 0,6.
Для чего в формулу (3.28) введен коэффициент KFθ? Имеется ли он в аналогичных формулах для проектного расчета зубьев на изгиб прямозубой и косозубой передач?
Расчет конических прямозубых передач на контактную прочность
3.77. В основу данного расчета берется формула (3.20) в параметрах эквивалентной цилиндрической прямозубой передачи по среднему дополнительному конусу
Используем связь тригонометрических функций, формул для определения передаточного числа (см. шаг 3.68) и делительного диаметра эквивалентного колеса dvei = dei /cosδ1.
После подстановки в исходную формулу значений dvl и uv и несложных преобразований получим формулу проверочного расчета для стальных прямозубых конических колес
(3.30)
или, заменив Ft=2T2/d1u; b = Ψbdd1, получим:
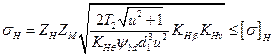
Z = ZH · ZM = 462 • 103 Па1/2 (для стальных колес), (3.31)
где σн — возникающее нормальное контактное напряжение, МПа; d1 — средний делительный диаметр шестерни, мм; Т2 — вращающий момент на колесе, Н · мм; ZH — коэффициент, учитывающий форму сопряжения поверхности зубьев; ZM — коэффициент, учитывающий механические свойства материала; Ψbd — коэффициент ширины (длины) зуба (см. шаг 3.71); и — передаточное число; КHθ = 0,85 — коэффициент, учитывающий снижение контактной прочности конической передачи по сравнению с прямозубой; [σ]н — допускаемое контактное напряжение (см. шаг 3.45). Из двух значений [σ]н выбирается меньшее.
Каким образом можно снизить нормальное контактное напряжение в передаче, не изменяя силовых параметров передачи и передаточного числа?
3.78. Проектировочный расчет.
Решая уравнение (3.31) относительно d1 запишем
|
|
|
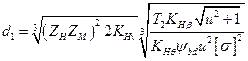
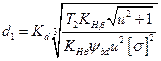(3.32)
где Kd =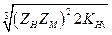 
— вспомогательный коэффициент (для стальных прямозубых конических колес Kd = 78 МПа1/3); (/„.мм; Т2, Н • мм; [σ]н, МПа.
Запишите в конспект формулы для определения [σ]H.
|
|
|
