 |
Разработка и принятие решений в условиях неопределенности и риска
|
|
|
|
Цель практической части курсовой работы
Выполнение расчётного задания с применением методов подготовки управленческого решения в условиях неопределенности и риска. Обоснование и выбор одной из альтернатив.
Постановка задачи
Таблица исходных данных к тестовой задаче
| № варианта | Затраты на НИОКР и внедрение новой продукции, млн. руб./ год | Эффект от использования новой продукции, млн. руб./ год | Затраты на модернизацию продукции, млн. руб./ год | Эффект от использования модернизированной продукции, млн. руб. / год | Априорные вероятности «состояний природы» | Условные вероятности исходов эксперимента |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 12 | 1,2 | 6 | 0,6 | 1,4 | 0,25;0,50;0,25 | 0,25 0,80 0,20 0,15 0,10 0,70 0,65 0,25 0,15 |
Рассматривается фирма, занимающаяся созданием и эксплуатацией наукоёмкой продукции. Перед руководством фирмы возникла проблема: следует ли принять решение о разработке новой продукции, то есть о проведении научно-исследовательских и опытно-конструкторских работ (НИОКР), или же отказаться от разработки новой продукции в пользу решения о проведении модернизации ранее выпущенной продукции. Ресурсы фирмы ограничены настолько, что заниматься разработкой новой и модернизацией ранее выпущенной продукции одновременно не представляется возможным. Принятие решения осложняется тем, что продолжительность разработки и внедрения новой продукции точно не известна и является дискретной случайной величиной (5, 10 или 15 лет).
Таким образом, решение принимается в условиях неопределённости и связано с риском непроизводительных затрат в рассматриваемом пятнадцатилетнем горизонте планирования.
Формализация задачи методами теории игр
|
|
|
Расчёты затрат и экономического эффекта (млн. руб.) в зависимости от продолжительности разработки, внедрения и использования новой продукции до конца 15-летнего планового периода удобно представить в виде таблицы возможных ситуаций.
Таблица ситуаций
| Решение планового органа | Продолжительность разработки, лет | Затраты на НИОКР и внедрение | Эффект от использования новой продукции | Затраты на модернизацию продукции | Эффект от использования модернизированной продукции | Суммарный эффект |
| Прово- дить НИОКР | 5 | -6 | 60 | -6 | 14 | 62 |
| 10 | -12 | 30 | -3 | 7 | 22 | |
| 15 | -18 | 0 | 0 | 0 | -18 | |
| Не про- водить НИОКР | 5 | 0 | 0 | -9 | 21 | 12 |
| 10 | 0 | 0 | -9 | 21 | 12 | |
| 15 | 0 | 0 | -9 | 21 | 12 |
Перейдём от неё к «платёжной» матрице игры, которую будем называть матрицей эффектов.
Матрица эффектов
| Решение планово-го органа | Состояние природы | ||
| В1 | В2 | В3 | |
| А1 | 62 | 22 | -18 |
| А2 | 12 | 12 | 12 |
Где А={А1,А2} – множество решений планирующего органа;
А1 – соответствует решению о проведении НИОКР;
А2 – соответствует решению об отказе от НИОКР;
В={В1,В2,В3} – множество состояний «природы», олицетворяющее неопределенность ситуации,
В1 – проведение НИОКР потребует 5 лет;
В2 – проведение НИОКР потребует 10 лет;
В3 – проведение НИОКР потребует 15 лет.
Рассматриваемая задача решается методами математической теории игр с использованием «платёжной» матрицы (матрицы эффектов либо матрицы потерь) и выбранных критериев принятия решения поэтапно:
– в условиях полной неопределённости;
– в условиях частичной определённости;
– в условиях эксперимента, предшествующего принятию решения;
– с применением аппарата решающих функций и использованием функции риска.
Решение задачи
Критерии принятия решений в условиях полной неопределённости.
Критерий Уолда
| Решение планового органа | Минимум выигрыша |
| А1 | -18 |
| А2 | 12* |
|
|
|
EY = maxi minj eij
Максимаксный критерий
| Решение планового органа | Максимум выигрыша |
| А1 | 62* |
| А2 | 12 |
EM = maxi maxj eij
Критерий Гурвича
| Решение планового органа | Степень оптимизма a | |||||||
| 0 | 0,2 | 0,3 | 0,4 | 0,6 | 0,8 | 1 | 0 | |
| А1 | -18 | -2 | 6 | 14 | 30 | 46 | 62 | -18 |
| А2 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
Критерий Сэвиджа
| Решение планового органа | Состояние природы | Максимум сожаления | ||
| В1 | В2 | В3 | ||
| А1 | 0 | 0 | 30 | 30 |
| А2 | 50 | 10 | 0 | 50 |
EC = mini maxj (maxi eij - eij)
Критерий Лапласа
| Решение планового органа | Равновероятный выигрыш |
| А1 | 22* |
| А2 | 12 |
n
EЛ = maxi S (eij / n)
j=1
Критерий принятия решений в условиях частичной определённости.
Условия частичной определенности предполагают, что распределение вероятностей состояний «природы» p(bj) известно и статистически устойчиво. В соответствии с исходными данными это распределение имеет вид:
p(b1) =0,25 p(b2) =0,50 p(b3) =0,25
Критерий Байеса-Лапласа
| Решение планового органа | Математическое ожидание выигрыша |
| А1 | 22* |
| А2 | 12 |
Принятие решений в статистических играх с экспериментом.
Принятию решения предшествует эксперимент. Допустим, что результаты эксперимента образуют множество X = {x1, x2, x3}, где исход эксперимента x1 означает, что проведение данной НИОКР потребует 5 лет, x2 – соответственно 10 лет и x3 – 15 лет. Как правило, такие результаты эксперимента носят не достоверный, а вероятностный характер. Это приводит к необходимости использования условных вероятностей p(xi/bj), которые показывают вероятность прихода к выводу xi, если на самом деле имеет место состояние «природы» bj.
В соответствии с исходными данными условные вероятности p(xi/bj) исходов эксперимента:
p(x1/b1) = 0,25 p(x1/b2) =0,80 p(x1/b3) =0,20
p(x2/b1) = 0,15 (x2/b2) =0,10 p(x2/b3) =0,70
p(x3/b1) =0,65 p(x3/b2) =0,25 p(x3/b3) =0,15
Находим полные вероятности исходов эксперимента:
p(x1) = p(x1/b1)p(b1) + p(x1/b2)p(b2) + p(x1/b3)p(b3)
p(x2) = p(x2/b1)p(b1) + p(x2/b2)p(b2) + p(x2/b3)p(b3)
p(x3) = p(x3/b1)p(b1) + p(x3/b2)p(b2) + p(x3/b3)p(b3)
p(x1) = 0,25×0,25+0,80∙0,50+0,20∙0,25=0,5125
p(x2) = 0,15×0,25+0,10∙0,50+0,70∙0,25=0,2625
p(x3) =0,65×0,25+0,25∙0,50+0,15∙0,25=0,325
Находим апостериорные вероятности состояния природы после того или иного исхода эксперимента (по формуле Байеса):
p(bj / xi) = p(xi / bj) p(bj) / p(xi)
|
|
|
p(b1/x1) = p(x1/b1)p(b1)/p(x1) =0,25∙0,25/0,5125≈0,1220
p(b2/x1) = p(x1/b2)p(b2)/p(x1) = 0,80∙0,50/0,5125≈0,7805
p(b3/x1) = p(x1/b3)p(b3)/p(x1) =0,20∙0,25/0,5125≈0,0976
p(b1/x2) = p(x2/b1)p(b1)/p(x2) =0,15∙0,25/0,2625≈0,1429
p(b2/x2) = p(x2/b2)p(b2)/p(x2) = 0,10∙0,50/0,2625≈0,1905
p(b3/x2) = p(x2/b3)p(b3)/p(x2) =0,70∙0,25/0,2625≈0,6667
p(b1/x3) = p(x3/b1)p(b1)/p(x3) = 0,65∙0,25/0,325=0,5
p(b2/x3) = p(x3/b2)p(b2)/p(x3) = 0,25∙0,50/0,325≈0,3846
p(b3/x3) = p(x3/b3)p(b3)/p(x3) =0,15∙0,25/0,325≈0,1154
Таким образом:
p(b1/x1) = 0,1220 p(b2/x1) = 0,7805 p(b3/x1) = 0,0976
p(b1/x2) = 0,1429 p(b2/x2) = 0,1905 p(b3/x2) = 0,6667
p(b1/x3) = 0,5 p(b2/x3) = 0,3846 p(b3/x3) = 0,1154
Находим по критерию Байеса-Лапласа (с учётом уже апостериорных вероятностей состояний «природы» p(bj / xi)) ожидаемые выигрыши для каждого исхода эксперимента:
62∙0,1220+22∙0,7805+(-18)∙0,0976=22,97561* Þ А1
EБ (x1) = max
12∙0,1220+12∙0,7805+12∙0,0976=12
62∙0,1429+22∙0,1905+(-18)∙0,6667=1,047619
EБ (x2) = max
12∙0,1429+12∙0,1905+12∙0,6667≈12*Þ А1
62∙0,5+22∙0,3846+(-18)∙0,1154=39,6*Þ А2
EБ (x3) = max
12∙0,5+12∙0,3846+12∙0,1154=12
Средний выигрыш при неизвестном заранее исходе эксперимента равен:
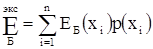
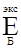=» 22,97561∙0,5125+12∙0,2625+39,6∙0,3125=27,3
При этом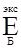 
=27,3 > Е = 22, то есть средний выигрыш с экспериментом больше, чем выигрыш без эксперимента.
Принятие решений в статистических играх в условиях риска.
В задаче без эксперимента решение (А1 или А2) принимается с использованием априорной информации о состояниях «природы». В задаче с экспериментом плановый орган принимает решение в зависимости от исхода эксперимента (Х1, Х2, Х3). Чтобы формализовать эту задачу, можно заранее проанализировать все возможные исходы эксперимента и составить правило d, определяющее, какое решение следует принять при каждом из возможных исходов эксперимента. Это правило называется решающей функцией.
В рассматриваемом случае (для трёх возможных исходов эксперимента) решающую функцию можно записать в виде
dkls = d (x1, x2, x3) = (Ak, Al, As),
где Ak, Al, As – решения, которые следует принять при исходах эксперимента x1, x2, x3 соответственно. Так, решающая функция d112 означает, что соответствие исходов и решений имеет вид
{ x1 ® A1, x2 ® A1, x3 ® A2 }, то есть при оценке срока НИОКР в 5 или 10 лет принимается решение о разработке новой продукции A1, а в 15 лет – решение об отказе от разработки новой продукции A2.
|
|
|
Множество решающих функций состоит из N = mq элементов, где m - число возможных решений; q – число возможных исходов эксперимента.
В нашем случае m = 2; q = 3; N = mq = 23 = 8 (см. таблицу).
|
|
|
