 |
Множество решающих функций
|
|
|
|
| Результаты эксперимента | d111 | d112 | d121 | d122 | d211 | d212 | d221 | d222 |
| X1 | A1 | A1 | A1 | A1 | A2 | A2 | A2 | A2 |
| X2 | A1 | A1 | A2 | A2 | A1 | A1 | A2 | A2 |
| X3 | A1 | A2 | A1 | A2 | A1 | A2 | A1 | A2 |
Из всего множества решающих функций необходимо выбрать такую, которая позволит принимать наиболее выгодные решения. Но для этого надо уметь оценивать сами решающие функции, что может быть сделано при помощи функции риска.
Функцией риска r(bj, dkls) называются средние потери, которые несёт плановый орган при данном состоянии природы и выбранной решающей функции. Число значений функции риска равно N×n, где n – число состояний природы. В нашем случае N = 8, n = 3, тогда 8×3 = 24.
Усреднение потерь ведётся по вероятностям исходов эксперимента при данном состоянии природы. В нашем случае:
r(bj, dkls) = П(bj, Ak)×p(x1/bj) + П(bj, Al)×p(x2/bj) + П(bj, As)×p(x3/bj)
или r(bj, dkls) = Пjk×p(x1/bj) + Пjl×p(x2/bj) + Пjs×p(x3/bj),
где Пjk, Пjl, Пjs – элементы матрицы потерь которые получаются из матрицы эффектов путём умножения её элементов на (-1). Отрицательные элементы Пji матрицы потерь означают получение экономического эффекта.
Матрица потерь
| Состояние природы | Решение планового органа | |
| А1 | А2 | |
| B1 | -62 | -12 |
| B2 | -22 | -12 |
| B3 | 18 | -12 |
Значения функции риска
| Состояние природы | d111 | d112 | d121 | d122 | d211 | D212 | d221 | d222 |
| В1 | -65,1 | -32,6 | -57,6 | -25,1 | -52,6 | -20,1 | -45,1 | -12,6 |
| В2 | -25,3 | -22,8 | -24,3 | -21,8 | -17,3 | -14,8 | -16,3 | -13,8 |
| В3 | 18 | 15 | -3 | -6 | 12 | 9 | -9 | -12 |
Расчёт значений функции риска
r(b1,d111) = -62∙0.25-62∙0.15-62∙0.65=-65.1
r(b1,d112) = -62∙0.25-62∙0.15-12∙0.65=-32.6
r(b1,d121) = -62∙0.25-12∙0.15-62∙0.65=-57.6
r(b1,d122) = -62∙0.25-12∙0.15-12∙0.65=-25.1
r(b1,d211) = -12∙0.25-62∙0.15-62∙0.65=-52.6
r(b1,d212) = -12∙0.25-62∙0.15-12∙0.65=-20.1
r(b1,d221) = -12∙0.25-12∙0.15-62∙0.65=-45.1
r(b1,d222) = -12∙0.25-12∙0.15-12∙0.65=-12.6
|
|
|
r(b2,d111) =-22∙0.80-22∙0.10-22∙0.25=-25.3
r(b2,d112) =-22∙0.80-22∙0.10-12∙0.25=-22.8
r(b2,d121) =-22∙0.80-12∙0.10-22∙0.25=-24.3
r(b2,d122) =-22∙0.80-12∙0.10-12∙0.25=-21.8
r(b2,d211) =-12∙0.80-22∙0.10-22∙0.25=-17.3
r(b2,d212) =-12∙0.80-22∙0.10-12∙0.25=-14.8
r(b2,d221) =-12∙0.80-12∙0.10-22∙0.25=-16.3
r(b2,d222) =-12∙0.80-12∙0.10-12∙0.25=-13.8
r(b3,d111) = 18∙0.20+18∙0.70+18∙0.15≈18
r(b3,d112) = 18∙0.20+18∙0.70-12∙0.15≈15
r(b3,d121) = 18∙0.20-12∙0.70+18∙0.15≈-3
r(b3,d122) = 18∙0.20-12∙0.70-12∙0.15≈-6
r(b3,d211) =-12∙0.20+18∙0.70+18∙0.15≈12
r(b3,d212) =-12∙0.20+18∙0.70-12∙0.15≈9
r(b3,d221) =-12∙0.20-12∙0.70+18∙0.15≈-9
r(b3,d222) =.-12∙0.20-12∙0.70-12∙0.15≈-12
Наилучшей решающей функцией будет та, которая обеспечивает минимум так называемому байесовскому риску, рассчитываемому по формуле:
r(dkls) = r(b1, dkls)×p(b1) + r(b2, dkls)×p(b2) + r(b3, dkls)×p(b3).
Определим байесовские риски для каждой из решающих функций:
r(d111) = -65.1∙0.25+(-25.3)∙0.5+18∙0.25=-24.425
r(d112) = -32.6∙0.25+(-22.8)∙0.5+15∙0.25=-15.8
r(d121) = -57.6∙0.25+(-24.3)∙0.5+(-3)∙0.25=-27.3
r(d122) =-25.1∙0.25+(-21.8)∙0.5+(-6)∙0.25=-18.675
r(d211) = -52.6∙0.25+(-17.3)∙0.5+12∙0.25=-18.8
r(d212)=-20.1∙0.25+(-14.8)∙0.5+9∙0.25=-10.175
r(d221) =-45.1∙0.25+(-16.3)∙0.5+(-9)∙0.25=-21.675
r(d222) =-12.6∙0.25+(-13.8)∙0.5+(-12)∙0.25=-13.05
Байесовские риски для различных решающих функций
| Решающая функция | d112 | d112 | d121 | d122 | d211 | d212 | d221 | d222 |
| Байесовский риск | -24,425 | -15,8 | -27,3 | -18,675 | -18,8 | -10,175 | -21,675 | -13,05 |
Умножая полученные байесовские риски на (-1), получим таблицу средних значений эффектов для различных решающих функций
Средние экономические эффекты для различных решающих функций, млн. руб.
| Решающая функция | d111 | d112 | d121 | d122 | d211 | D212 | d221 | d222 |
| Средний эффект | 24.425 | 15.8 | 27.3 | 18.675 | 18.8 | 10.175 | 21.675 | 13.05 |
Построим график среднего экономического эффекта в зависимости от выбранной решающей функции. На оси абсцисс графика с равным шагом отмечаются точками решающие функции в той последовательности, в которой они приведены в таблице, а вдоль оси ординат – в выбранном масштабе для каждой решающей функции строятся точки средних значений экономического эффекта.
|
|
|
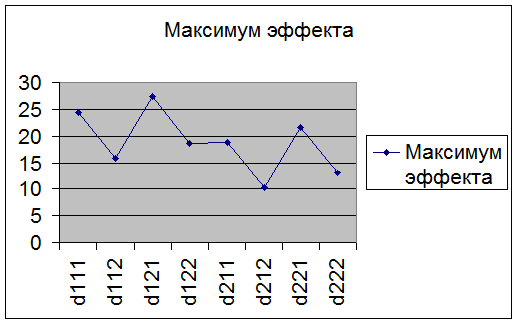 |
В результате последовательного соединения найденных точек прямыми линиями получается пилообразный график-диаграмма.
Выводы
В ходе выполнения практической части работы были рассмотрены различные способы и критерии разработки и принятия решений о целесообразности разработки новой продукции в условиях неопределенности.
Минимум байесовского риска (максимум эффекта) достигается при использовании решающей функции d121. Она и является наилучшей. Этот же результат получен и при нахождении среднего выигрыша в п. 4.3. без использования понятий риска и решающей функции, что подтверждает правильность выполненных расчётов.
Наихудшей решающей функцией является d212. При таком абсурдном поведении планового органа величина среднего эффекта ниже, чем даже при полном отказе от разработок новой продукции при любых условиях (пассивное поведение d222).
ЗАКЛЮЧЕНИЕ
В процессе написания моей курсовой, я рассмотрела в теоретической части тему: «Моделирование, как метод разработки управленческого решения».
Материал, подобранный мной, по этой теме помог ответить мне на интересующий меня вопрос: «Для чего в процессе принятия управленческих решений, необходимо моделирование?»
В практической части, в данной задаче, научилась применять знания, полученные на лекциях по данному предмету, на практике, а именно пришла к принятию решения в условиях неопределенности и риска, с помощью определенных расчетов.
На мой взгляд, в моей курсовой все поставленные мною задачи выполнены, основная цель достигнута.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Глущенко В.В. Менеджмент: системные основы. – 2-е изд. – Железнодорожный: ТОО НПЦ «Крылья», 1998. – 224 с.
2. Литвак Б.Г. Разработка управленческого решения: Учебник. – 3-е изд., испр. – М.: Дело, 2002. – 392 с.;
3. Ременников В.Б. Разработка управленческого решения: Учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2000. – 140 с.;
4. Смирнов Э.А. Разработка управленческих решений: Учебник для вузов. – М.: ЮНИТИ – ДАНА, 2000. – 271 с.
|
|
|


