 |
Методические положения оценки согласованности мнения экспертов с применением коэффициента конкордации.
|
|
|
|
Лабораторная работа №4
Оценка согласованности мнений экспертов с применением коэффициента конкордации
1. Цель и содержание лабораторной работы.
Цель лабораторной работы - освоение студентами знаний для самостоятельного использования методов экспертных оценок в управлении с целью принятия оптимальных управленческих решений, приобретение практических навыков проведения экспертизы и оценки согласованности мнений экспертов с применением коэффициента конкордации.
При проведении различных выборочных исследований (маркетинговых, клинических, эпидемиологических, социологических) очень часто возникает необходимость оценить согласованность мнений экспертов. Это в дальнейшем позволяет, во-первых, выявить различные подходы экспертов к оценке различных явлений (признаков, критериев), во-вторых, провести углубленный анализ ситуации и принять обоснованное решение.
Необходимо провести экспертизу, заключающуюся в выявлении степени влияния различных факторов на финансово-экономическую деятельность предприятия. С этой целью студенты делятся на две группы и выступают в роли экспертов.
Первая группа выявляет те факторы, которые отражают влияние внутренней среды предприятия, а вторая группа – внешней среды. Каждая группа формирует матрицу исходных данных, где в качестве объекта берутся соответствующие факторы, влияющие на финансово-экономическую деятельность предприятия. Каждый студент, выступая в роли эксперта, должен выявленным факторам присвоить соответствующий балл, оценивая степень влияния на деятельность предприятия по десяти - балльной шкале.
Затем эксперты обеих групп оценивают с использованием коэффициента конкордации согласованность мнений и делают соответствующие выводы.
|
|
|
Методические положения оценки согласованности мнения экспертов с применением коэффициента конкордации.
В связи с природой данных, которые являются результатами экспертных оценок (обычно баллы), для их анализа обычно используются ранговые (непараметрические) методы.
Для того чтобы оценить согласованность мнений двух экспертов при их оценке ряда признаков (или объектов, что имеет значение при решении задачи ранжирования), можно воспользоваться коэффициентом корреляции Спирмена или коэффициентом корреляции Кендалла.
В случае если экспертов не два, а более (например, при выяснении согласованности мнений группы экспертов), используется дисперсионный коэффициент конкордации:
 , (3.1)
, (3.1)
где  , (3.2)
, (3.2)
n - количество анализируемых объектов,
m - количество экспертов,
Rij- ранг j -го объекта, который присвоен ему i -ым экспертом.
Дисперсионный коэффициент конкордации рассчитывают по матрице ранжировок n объектов группой из m экспертов, где rij - ранг, присвоенный j- ым экспертом i- ому объекту.
Следует обратить внимание на отличие значений коэффициента конкордации от коэффициента корреляции, так как он существует в пределах от 0 до 1. Если мнения экспертов полностью противоположны, коэффициент конкордации равен нулю (W = 0), а коэффициент корреляции в этом случае будет равен -1.
Приналичииодинаковых связанных рангов формула (3.1) приобретает следующий вид:
 , (3.3)
, (3.3)
 , (3.4)
, (3.4)
 , (3.5)
, (3.5)
где Тj – показатель связанных (одинаковых) рангов в j- ой ранжировке,
Hj – число групп равных рангов в j- ой ранжировке;
hk – число равных рангов в k- ой группе связанных рангов при ранжировке j- ым экспертом,
n – число объектов,
m – число экспертов
rij- ранг, присваиваемый j- ым экспертом i- ому объекту;
 - средний ранг, равный
- средний ранг, равный 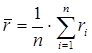 .
.
Если коэффициент конкордации равен 1, то все ранжировки экспертов одинаковы; а W = 0, если все ранжировки различны, то совершенно нет совпадений. Мнения экспертов согласованны, если W > 0,6. Если W < 0,6, анализируют ответы на согласованность мнений, выявляют дополнительные факторы, которые необходимо учесть экспертам, определяют экспертов, мнение которых максимально расходится с общим мнением.
|
|
|
|
|
|


