 |
Указания к выполнению заданий № 6-8.
|
|
|
|
См. [1, стр. 81-153]; [2, стр. 32-44]; [3, стр. 37-68]; [4, стр. 51-81]; [5, стр. 319-322]; [6, стр. 27-57].
Величина адсорбции зависит от природы поверхности адсорбента, природы адсорбата и его концентрации (давления), температуры и др. графическая зависимость адсорбции от концентрации адсорбируемого вещества в объемной фазе при данной температуре называется изотермой адсорбции.
Адсорбция из предельно разбавленных растворов или смесей газов подчиняется закону Генри:
А = КГ . С или А = К¢Г . Р, (1)
где КГ и К¢Г - константа Генри;
С - концентрация адсорбата в объемной фазе;
Р - давление пара адсорбата.
Аналитическим выражением изотермы мономолекулярной адсорбции при более высоких концентрациях и ровной поверхности является уравнение изотермы Ленгмюра:
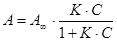 или
или 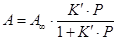 , (2)
, (2)
где К и К¢ - константы адсорбционного равновесия, характеризующие энергию адсорбции;
А¥ -предельная мономолекулярная адсорбция - емкость монослоя, А¥ = n/NА;
n - число молекул на 1 м2 адсорбированного слоя при максимальной упаковке;
NА - число Авогадро.
 А
А
|


 А¥
А¥
 | |||
 |
С(Р)
Константы А¥ и К можно найти графически преобразовав уравнение (2), получим:
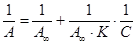 ,
, 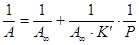 (3)
(3)
или
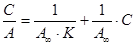 (4)
(4)


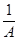
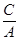
 |  | ||
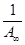

 |  |
C 1/C
Рисунок 2 – Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра.
1/A¥. К для уравнения (3) или 1/A¥ для уравнения (4) находят как тангенс угла наклона прямой к оси С или 1/C, соответственно (как отношение стороны противолежащей к стороне прилежащей, см. пояснения к контрольным заданиям по физической хиии).
|
|
|
Если адсорбируется газ, то уравнение (3) может принимать вид:
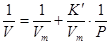 (5)
(5)
или
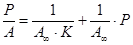 (6)
(6)
где v - объем адсорбированного газа;
vm - объем адсорбированного газа, полностью, покрывающего поверхность 1 г адсорбента.
Если принять экспоненциальное распределение неоднородностей поверхности, то как показал Я. Б. Зельдович, в области средних заполнений получается ранее найденное эмпирически уравнение Фрейндлиха:
A = K . P1/n , (7)
где K и n - постоянные.
Уравнение Фрейндлиха широко используется при обработке экспериментальных адсорбционных данных и инженерных расчетах, чаще оно применяется в логарифмической форме:
ln A = ln K + (1/n) . ln P, (8)
позволяющей построить линейную зависимость ln A - ln P и графически определить оба параметра K и n. вместо А иногда пишут x/m,где х - количество адсорбированного вещества; m - масса адсорбента. Для растворов уравнения (7) и (8) принимают вид:
x/m = K . Cn (9)
или ln(x/m) = ln K + n ln C. (10)
график для уравнения (10) принимает вид, аналогичный приведенному на рисунке 2.
Предполагая многослойную адсорбцию, Брунауэр, Эммет и Теллер вывели уравнение изотермы адсорбции (БЭТ):
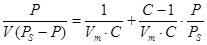 , (11)
, (11)
где v - общий объем адсорбированного газа;
vm - объем адсорбированного газа, если вся поверхность адсорбента покрыта сплошным мономолекулярным слоем;
Р - равновесное давление адсорбированного газа;
Р - давление насыщенного пара;
С - константа при данной температуре.
Согласно уравнению (11) зависимость 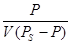 от
от  на графике дает прямую линию с тангенсом угла наклона
на графике дает прямую линию с тангенсом угла наклона 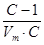 .
.
При выполнении задания № 8 можно воспользоваться примером решения аналогичной задачи.
Пример. Рассчитать удельную поверхность адсорбента по изотерме адсорбции бензола на его поверхности. Площадь, занимаемая молекулой бензола, S0 = 49 . 10-20 м2.
| Р/PS | 0,024 | 0,08 | 0,14 | 0,20 | 0,27 | 0,35 | 0,46 |
| A.103, моль/кг | 14,9 | 34,8 | 47,2 | 56,8 | 66,3 | 79,3 | 101,0 |
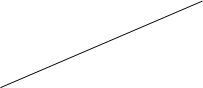
Решение. Проверяют применимость к экспериментальным данным теории БЭТ. С этой целью рассчитывают абсциссу и ординату уравнения изотермы адсорбции БЭТ в линейной форме, т. е.
|
|
|
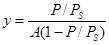 и x = P/PS.
и x = P/PS.
Результаты вычислений сводят в таблицу 9 и строят график зависимости y = f(x) (рисунок 3).
Таблица 9. Данные для проверки теории БЭТ
| Р/PS | 0,024 | 0,08 | 0,14 | 0,20 | 0,27 | 0,35 | 0,46 |
| y, кг/моль | 1,650 | 2,499 | 3,449 | 4,400 | 5,466 | 6,790 | 8,434 |
Для определения адсорбционной емкости монослоя А¥ по графику зависимости y = f(x) находят константы уравнения прямой линии: отрезок, отсекаемый на оси ординат при Р/PS = 0, b0 =1,24 кг/моль, и угловой коэффициент прямой b1 = 15,8 кг/моль. Для сравнения вычисляют b0 и b1, пользуясь методом наименьших квадратов. Данные для расчета b0 и b1 приведены в табл. 10.
Константы b0 и b1 рассчитывают по формулам (12) и (13):
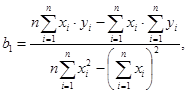 (12)
(12)
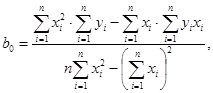 (13)
(13)
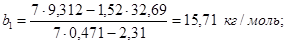
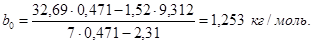
 |
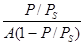

 P/PS
P/PS
Рисунок 3 – Изотерма адсорбции в координатах линейной формы уравнения БЭТ (14).
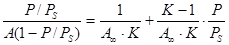 (14)
(14)
Таблица 10 – Данные для вычисления констант b0 и b1.
| n | x | y, кг/моль | xy, кг/моль | x2 |
| 0,024 | 1,650 | 0,0396 | 5,76.10-4 | |
| 0,080 | 2,499 | 0,2000 | 6,4.10-3 | |
| 0,140 | 3,449 | 0,4830 | 1,96.10-2 | |
| 0,200 | 4,400 | 0,8800 | 4,00.10-2 | |
| 0,270 | 5,456 | 1,4550 | 7,08.10-2 | |
| 0,350 | 6,790 | 2,3765 | 0,123 | |
| 0,460 | 8,434 | 3,8778 | 0,212 |
Решая систему уравнений
 (A¥K)-1 = b0,
(A¥K)-1 = b0,
(k-1) (A¥K)-1 = b1,
находят K = 13,65 и A¥ = 0,0489 моль/кг.
По величине A¥, рассчитывают удельную поверхность адсорбента:
S = S0 A¥NA = 49 . 10-20. 0,0489 . 6,02 . 1023 = 14,4 . 103 м2/кг.
3 образование и строение двойного электрического слоя. электрокинетические явления в дисперсных системах
ЗАДАНИЕ № 9
1. Вычислить x -потенциал с учетом поверхностной проводимости на границе раздела кварцевая диафрагма-раствор хлорида калия и построить график зависимости x от концентрации электролита по следующим данным:
| С. 10-3, моль/м3 | 0,05 | 0,1 | 0,5 | 1,0 |
| cv. 102, Ом-1.м-1 | 1,0 | 2,06 | 2,24 | 6,0 |
| Uтеч. 103, В | 10,01 | 8,5 | 7,0 | 3,1 |
| a | 3,25 | 1,5 | 1,3 | 1,05 |
e = 81; h = 1 . 10-3 Па . с; Р = 1,06 . 104 Па.
2. Рассчитать x -потенциал и построить график зависимости от диаметра пор кварцевой диафрагмы в растворе хлорида калия без учета поверхностной проводимости и с учетом ее по следующим данным:
| d. 106, м | ||||||
| v. 108, м3/с | 1,2 | 1,5 | 2,0 | 2,8 | 3,5 | 0,12 |
| cs. 102, Ом-1 . м-1 | 3,22 | 2,25 | 1,32 | 0,52 | 0,12 | 0,075 |
cv = 1,5 . 10-2 Ом-1. м-1; I = 2 . 10-2 А; e = 81; h = 1 . 10-3 Па . с.
3. Построить графики зависимости x- потенциала от диаметра пор кварцевой диафрагмы без учета поправки на поверхностную проводимость и с учетом ее по следующим данным:
|
|
|
| d. 106, м | ||||
| v. 108, м3/с | 1,2 | 2,4 | 3,4 | 3,7 |
| cs. 102, Ом-1 . м-1 | 3,1 | 2,08 | 1,08 | 1,01 |
cv = 1,6 . 10-2 Ом-1. м-1; I = 3,2 . 10-2 А; e = 81; h = 1 . 10-3 Па . с.
4. Рассчитать x -потенциал корундовой диафрагмы в растворе хлорида натрия и построить график зависимости x от диаметра пор диафрагмы по следующим данным:
| d. 106, м | |||||
| v. 108, м3/с | 2,8 | 3,2 | 3,6 | 3,9 | 4,0 |
| cs. 102, Ом-1 . м-1 | 1,48 | 1,30 | 1,15 | 1,05 | 1,02 |
cv = 1,6 . 10-2 Ом-1. м-1; I = 2 . 10-2 А; e = 81; h = 1 . 10-3 Па . с.
5. Рассчитать x -потенциал керамической диафрагмы в растворе хлорида натрия и построить график зависимости x от диаметра пор диафрагмы по следующим данным:
| d. 106, м | |||||||
| v. 108, м3/с | |||||||
| cs. 102, Ом-1 . м-1 | 2,93 | 2,50 | 1,71 | 1,34 | 1,23 | 1,08 | 1,06 |
cv = 1,5 . 10-2 Ом-1. м-1; I = 2 . 10-2 А; e = 81; h = 1 . 10-3 Па . с.
6. Рассчитать x -потенциал и построить график зависимости x от диаметра пор корундовой диафрагмы в растворе хлорида калия без учета и с учетом поверхностной проводимости по следующим данным:
| d. 106, м | ||||
| v. 108, м3/с | 2,0 | 3,2 | 3,9 | 4,0 |
| cs. 102, Ом-1 . м-1 | 1,6 | 0,48 | 0,08 | 0,03 |
cv = 1,6 . 10-2 Ом-1. м-1; I = 2 . 10-2 А; e = 81; h = 1 . 10-3 Па . с.
7. Рассчитать x -потенциал с учетом и без учета поверхностной проводимости и построить график зависимости x от диаметра керамической диафрагмы в растворе хлорида натрия по следующим данным:
| d. 106, м | ||||||
| v. 108, м3/с | 1,3 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
| cs. 102, Ом-1 . м-1 | 2,9 | 2,4 | 1,9 | 1,5 | 1,25 | 1,08 |
cv = 1,5 . 10-2 Ом-1. м-1; I = 2 . 10-2 А; e = 81; h = 1 . 10-3 Па . с.
8. Построить график зависимости потенциала течения от давления для кварцевой диафрагмы в растворе хлорида калия по следующим данным: р (Па) равно а) 5 . 103, б) 10 . 103, в) 15 . 103, г) 20 . 103, д) 25 . 103; x = 8 . 10-2 В; e = 81; h = 1 . 10-3 Па . с; cv =2,1 . 10-2Ом-1. м-1; a = 1,2.
9. Рассчитать скорость электрофореза частиц оксида алюминия в воде с учетом электрофоретического торможения по следующим данным: x = 20 . 10-3, В; Е = 5 . 102 В/м; e = 81; h = 1 . 10-3 Па . с; а = 5 . 10-7 м; c = 1,5 . 107 м-1.
|
|
|
10. Рассчитать скорость электрофореза частиц оксида алюминия в метаноле с учетом электрофоретического торможения по следующим данным: x = 30 . 10-3, В; Е = 8 . 102 В/м; e = 33; h = 0,8 . 10-3 Па . с; а = 1,5 . 10-8 м; c = 2 . 108 м-1.
11. Рассчитать потенциал течения через корундовую диафрагму в растворе хлорида калия, если известно, что скорость электрофореза частиц корунда, образующих диафрагму, в том же растворе без учета электрофоретического торможения равна 24 . 10-6 м/с; h = 1 . 10-3 Па . с; Е = 4 . 102 В/м; e = 81; а = 5 . 10-8 м; c = 2 . 108 м-1; Р = 4 . 103 Па; cv = 1,5 . 10-2 Ом-1. м-1; a = 1,5.
12. Рассчитать потенциал течения через диафрагму из частиц карбоната кальция в водном растворе хлорида натрия, если известно, что скорость электрофореза частиц карбоната в том же растворе без учета электрофоретического торможения равна 10 . 10-6 м/с; h = 1 . 10-3 Па . с; Е = 2 . 102 В/м; e = 81; а = 3 . 10-7 м; c = 1,5 . 107 м-1; Р = 5 . 103 Па; cv = 2,5 . 10-2 Ом-1. м-1; a = 1,2.
13. Рассчитать электрофоретическую подвижность частиц карбоната стронция в воде, если x, рассчитанный по скорости электрофореза без учета электрофоретического торможения, равен 50 . 10-3 В; h = 1 . 10-3 Па . с; Е = 4 . 102 В/м; e = 81; а = 3 . 10-7 м; c = 1,5 . 108 м-1; Р = 5 . 103 Па; а = 2 . 10-8 м.
14. Рассчитать скорость электроосмоса раствора хлорида калия через корундовую диафрагму, если известно, что x -потенциал, рассчитанный по скорости электрофореза частиц корунда в том же растворе без учета электрофоретического торможения, равен 35 . 10-3 В; h = 1 . 10-3 Па . с; Е = 2 . 102 В/м; e = 81; I = 2 . 10-2 A; ca = 3; Р = 5 . 103 Па; cv = 2 . 10-2 Ом-1. м-1; a = 1,1.
15. Вычислить x, если известно, что потенциал течения, определенный при продавливании раствора хлорида калия через корундовую диафрагму под давлением 20 . 103 Па, равен 22,5 . 10-3 В. Удельная проводимость раствора cv = 1,37 . 10-2 Ом-1. м-1, коэффициент эффективности диафрагмы a = 1,8; вязкость раствора h = 1 . 10-3 Па . с; e = 81.
16. Вычислить электрофоретическую подвижность частиц оксида железа по следующим данным скорость электроосмоса через диафрагму из таких же частиц в том же растворе v = 2 . 10-8 м/с; cv = 1,2 . 10-2 Ом-1. м-1; cs = 2 . 10-2 Ом-1. м-1; h = 1 . 10-3 Па . с; e = 81; I = 1,6 . 10-2 A.
17. Рассчитать массу осадка, полученного на цилиндрическом электроде при электрофорезе водной суспензии оксида железа. Длина электрода l = 2·10-2 м; радиус внутреннего электрода r2 = 1 . 10-3 м; радиус наружного r1 = 28 . 10-3 м; x = 20 . 10-3 В; напряжение на электродах U = 20 В; C0 = 0,5 . 103 кг/м3; h = 1 . 10-3 Па . с; e = 81; Cm = 1 . 10-3 кг/м3; t = 15 с.
18. Рассчитать массу осадка, полученного на цилиндрическом электроде при электрофорезе водной суспензии СаСО3. Длина электрода l = 2·10-2 м; радиус внутреннего электрода r2 = 1 . 10-3 м; радиус наружного r1 = 28 . 10-3 м; x = 25 . 10-3 В; напряжение на электродах U = 30 В; C0 = 0,3´ ´103кг/м3; h = 1 . 10-3 Па . с; e = 81; Cm = 1 . 10-3 кг/м3; t = 20 с.
|
|
|
19. Рассчитать массу электрофоретического осадка, полученного из водной суспензии глины на цилиндрическом электроде длиной l = 1·10-2 м и радиусом r2 = 0,5 . 10-3 м в ванне с наружным цилиндрическим электродом r1 = 14 . 10-3 м; x = 30 . 10-3 В; U = 5 В; C0 = 0,5 . 103 кг/м3; h = 1 . 10-3 Па . с; e = 81; Cm = 1 . 10-3 кг/м3; t = 10 с.
20. Рассчитать массу осадка, образовавшегося на электроде при электрофорезе водной суспензии корунда при напряженности электрического поля 1·102; 2·102; 4·102 В/м; концентрация суспензии C = 2,0 . 10-3 кг/м3, продолжительность осаждения t = 10 с; x-потенциала, определенный по скорости электроосмоса без учета поверхностной проводимости, равен 49,6 . 10-3 В; коэффициент эффективности диафрагмы равен 1,8; e = 81; поверхность плоского электрода S = 1 . 10-4 м2; h = 1 . 10-3 Па . с.
21. Рассчитать электрофоретическую подвижность частиц корунда в воде, если известно, что скорость электроосмоса через корундовую диафрагму в том же растворе составляет 2 . 10-8 м/с, удельная электрическая проводимость раствора cv = 1,2 . 10-2 Ом-1. м-1, поверхностная проводимость диафрагмы cs = 2 . 10-2 Ом-1. м-1; вязкость раствора h = 1 . 10-3 Па . с; сила тока при электроосмосе I = 4,25 . 10-2 A; e = 81.
22. Рассчитать потенциал седиментации частиц оксида алюминия в водном растворе хлорида калия по следующим данным: j = 0,1; e = 81; z = 50 . 10-3 B; r-r0 = 3 . 103 кг/м3; h = 1 . 10-3 Па . с; cv = 1 . 10-2 Ом-1. м-1.
23. Рассчитать потенциал течения и построить график его зависимости от концентрации электролита с по следующим данным:
| С. 10-3, моль/м3 | 0,1 | 0,5 | 1,0 | |
| cv. 102, Ом-1.м-1 | 2,13 | 20,6 | 79,4 | 154,0 |
| z . 103, B |
e = 81; h = 1 . 10-3 Па . с; Р = 5 . 103 Па; a = 1,0/
24. Под каким давлением должен продавливаться раствор хлорида калия через керамическую диафрагму, чтобы потенциал течения Uтеч составил 4·10-3 В; x = 30 . 10-3 В; e = 81; h = 1 . 10-3 Па . с; cv = 1,3 . 10-2 Ом-1. м-1; a = 1,5.
25. Вычислить x-потенциал по следующим данным: потенциал течения Uтеч = 45 . 104 В; Р = 4 . 10-3 Па; e = 81; h = 1 . 10-3 Па . с; cv = 1,5 . 10-2 Ом-1. м-1; a = 1,8.
26. Рассчитать электрокинетический потенциал с учетом поверхностной проводимости на границе раздела кварцевая диафрагма-раствор хлорида натрия и построить график зависимости x от концентрации электролита по следующим данным:
| С. 10-3, моль/м3 | 0,1 | 0,2 | 0,3 | 0,45 | 0,7 |
| cv. 102, Ом-1.м-1 | 2,0 | 3,0 | 3,5 | 3,7 | 4,0 |
| V. 109, м3/с | 5,1 | 3,1 | 1,1 | 0,7 | 0,2 |
e = 81; h = 1 . 10-3 Па . с; I = 4,0 . 10-3 A; a = 2.
27. Рассчитать электрокинетический потенциал с учетом поверхностной проводимости на границе раздела корундовая диафрагма-раствор хлорида калия и построить график зависимости x от концентрации электролита по следующим данным:
| С. 10-3, моль/м3 | 0,1 | 0,2 | 0,45 | 0,7 | 1,0 |
| cv. 102, Ом-1.м-1 | 2,0 | 2,5 | 2,8 | 3,0 | 3,5 |
| V. 109, м3/с | 1,5 | 1,0 | 0,5 | 0,25 | 0,1 |
e = 81; h = 1 . 10-3 Па . с; I = 4,0 . 10-3 A; a = 2.
|
|
|


