 |
Создание нечёткой экспертной системы в пакете CubiCalc
|
|
|
|
CubiCalc 2.0 – Программа фирмы HyperLogic, является одной из наиболее мощных экспертных систем на основе нечёткой логики. Пакет содержит интерактивную оболочку для разработки нечётких экспертных систем и систем управления.
Фактически пакет CubiCalc 2.0 представляет собой своего рода экспертную систему, в которой пользователь задает набор правил типа «если-то», а система пытается на основе этих правил адекватно реагировать на параметры текущей ситуации. Отличие состоит в том, что вводимые правила содержат нечёткие величины, т.е. имеют вид «если X принадлежит А, то Y принадлежит B», где A и В – нечёткие множества. Аппарат нечёткой логики, заложенный в CubiCalc, дает возможность оперировать нечёткими понятиями как точными и строить на их основе целые логические системы.
Рассмотрим следующий пример: необходимо оценить степень инвестиционной привлекательности конкретного бизнес-проекта (rate) на основании данных о ставке дисконтирования (discont) и периоде окупаемости (period).
Процесс разработки нечёткой экспертной системы в пакете CubiCalc начинается с определения переменных, которые будут использоваться в проекте project→variables→new (рис. 3.1).

Рис. 3.1 – Определение переменных
В CubiCalc доступны несколько типов переменных:
1) Fuzzy Input – входная переменная, на области значения которой задаются нечёткие множества, используемые в левой части правил вывода.
2) Fuzzy Output – результат работы системы нечёткого логического вывода, на интервале ее изменения определяются нечёткие множества, используемые в правой части правил вывода.
3) Constant – переменная с фиксированным значением.
4) Temporary – переменная, принимающая действительные значения (данному типу переменных соответствует тип «float»).
|
|
|
Объявляем первую переменную как discont (поле name), задаем атрибуты переменной: выберем ее тип (Fuzzy Input), зададим диапазон изменения ее значений [5, 50] (Range Low – нижняя граница диапазона, Range High – верхняя граница), а также зададим начальное значение Initial Value равное 5.
Нажмем на кнопку «ОК» и «discont» появится в списке переменных (рис. 3.2).
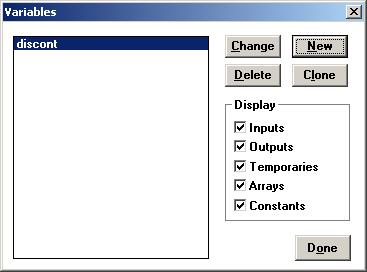
Рис. 3.2 – Окно списка переменных
Аналогично создадим вторую входную переменную – period с диапазоном изменения значений [3, 36]. Наименование выходной переменной, на основании которой принимается решение о степени инвестиционной привлекательности бизнес-проекта, задается как rate (диапазон изменения значений [0, 1]).
Далее необходимо задать характеристики всех трех переменных Project→ Adjective editor.
Выбрав переменную discont в окне «Adjectives for variables», нажмите кнопку Edit. Здесь каждой входной и выходной переменной поставим в соответствие набор функций принадлежности Adjective→ Change List→New. В появившемся окне «Create Adjective(s)» зададим следующие параметры: количество функций принадлежности (Number) равное 3; вид функции принадлежности (Shape) – triangle; ширина основания (base width) равная 45,0 (рис. 3.3).
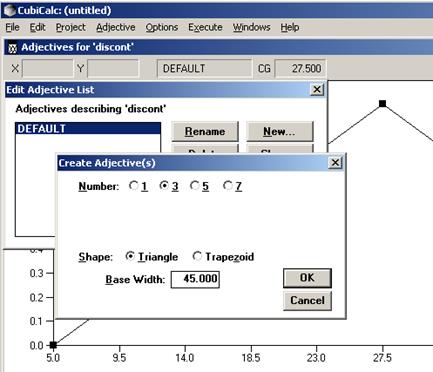
Рис. 3.3
В окне «Edit Adjective List» присвоим наименования – small, middle, big соответственно небольшой, средней и большой ставке дисконтирования (рис.3.4). Для переменной period зададим следующие параметры: количество функций принадлежности (Number) равное 3; вид функции принадлежности (Shape) – trapezoid; base width=33,0, crown width=8,25. В окне «Edit Adjective List» присвоим наименования – short, normal, long соответственно короткий, обычный и длительный срок окупаемости.
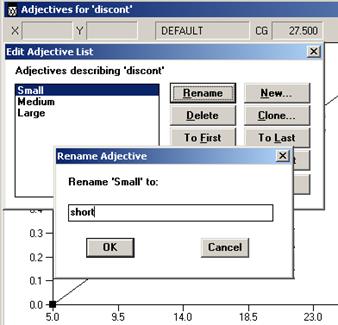
Рис. 3.4
Для переменной rate зададим следующие параметры: количество функций принадлежности (Number) равное 3; вид функции принадлежности (Shape) – triangle; base width=1. В окне «Edit Adjective List» присвоим наименования – bad, normal, good.
Далее необходимо определить набор правил, которые связывают входные переменные с выходными. Для этого в редакторе правил вывода Project→Rules определим:
|
|
|
IF discont is small AND period is short THEN rate is good;
IF discont is middle AND period is long THEN rate is bad;
IF discont is middle AND period is normal THEN rate is normal;
IF discont is big AND period is short THEN rate is normal;
Следующими этапами выполнения проекта в CubiCalc являются предобработка и постобработка. Предобработка (Project→Preprocessing) задает входные данные. Для этого используется функция field (), которая возвращает данные из отдельного поля текущей записи.
Откройте Preprocessing Editor (Редактор предобработки) и вставьте нижеследующие инструкции в его окно редактора:
discont = field(1);
period = field(2);
check = field(3);
В рассматриваемой нечёткой системе всего два входа, третья переменная (check) содержит «правильный ответ». Таким образом, мы можем посчитать количество ошибок, совершенных системой в классификации инвестиционной привлекательности бизнес-проекта.
В постобработке (Project→Postprocessing) задается метод автоматической оценки эффективности системы. Необходимо посчитать количество сделанных системой ошибок и вывести сумму в конце запуска. Чтобы обнаружить ошибку классификации в постобработке, необходимо сравнить выходную переменную с информацией check в файле данных.
Чтобы это сделать, вставьте нижеследующие инструкции в окно редактора:
If (rate <> check) errors += 1;end
If (endoffile=TRUE) call message(errors); end
Эти инструкции выполняют сравнение и дают приращение переменной errors, если происходит ошибка. Последняя инструкция выводит окно с сообщением, содержащим количество ошибок при достижении конца файла с входными данными.
В процессе настройки системы мы использовали переменные, отличные от входных и выходных. Для обнаружения ошибок классификации мы использовали переменную check и переменную errors для подсчета количества ошибок классификации. Теперь мы должны создать эти переменные.
Откройте Variables Editor с помощью меню Variables. Появится диалоговое окно, содержащее имена уже созданных входных и выходных переменных. Нажмите кнопку New для создания новой переменной.
В окне Edit Variable определите переменные: сheck (тип переменной – Temporary, начальное значение 0.0); errors (тип переменной – Temporary, начальное значение 0.0).
Настройка входного файла
Для присоединения входного файла к проекту, необходимо создать файл с расширением.txt (рис. 3.5), задать имя
|
|
|
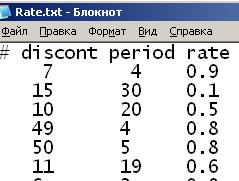
Рис. 3.5
файла (File→Input File) и некоторые его атрибуты (рис. 3.6).
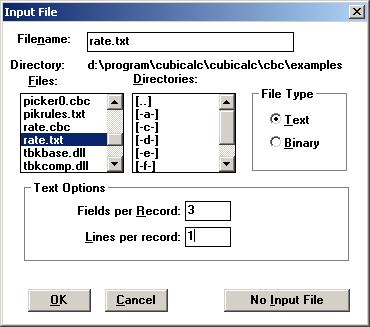
Рис. 3.6
Укажите Text для определения файла как текстового файла, содержащего печатаемые данные. Задайте количество Fields per Record (Полей на запись), равное 3 (каждая запись содержит значения для discont, period и check) и количество Lines per Record (Строк на запись), равное 1 (каждая запись занимает одну текстовую строку).
Далее необходимо определить, какая информация должна отображаться при запуске системы (Project→Log Format). Выберем нажатием кнопки «Add» из левого списка переменные discont, period, rate и check. Убедимся в непротиворечивости переменных (Execute→Check Definitions), снимем флажки Initialization, Simulation.
Проверим работу системы, запустив сценарий Execute→Run. Появится окно, содержащее значения переменных и их порядок, выбранные в Log Format Editor. Через некоторое время CubiCalc дойдет до конца входного файла и появится итоговое сообщение, заданное в предобработке. Выполните Execute→Terminate для остановки сценария.
Содержание работы
1. Постройте объединение, пересечение, разность нечётких множеств согласно варианту.
| Вариант | Исходные множества | Вариант | Исходные множества | Задание |
Постройте объединение нечётких множеств 
| ||||
Постройте пересечение нечётких множеств 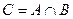
| ||||
Постройте пересечения 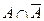 , , 
| ||||
Постройте разность нечётких множеств 
| ||||
Постройте разность нечётких множеств 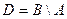
| ||||
Постройте пересечения 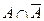 , , 
| ||||
Исходные множества
| Мно-жество | Множество А | Множество В |
| {(x1;0,7),(x2;0,5),(x3;0,3),(x4;0),(x5;0),(x6;0,2)} | {(x1;0),(x2;0,3),(x3;0,6),(x4;0,9),(x5;1,0),(x6;0)} | |
| {(x1;1,0),(x2;0,8),(x3;0),(x4;0),(x5;0)} | {(x1;0),(x2;0),(x3;0,4),(x4;0,7),(x5;0),(x6;0)} | |
| {(x1;0),(x2;0,3),(x3;0,3),(x4;0,5),(x5;0,2),(x6;0)} | {(x1;0,1),(x2;0,2),(x3;0,6),(x4;0,9),(x5;0,5),(x6;0)} | |
| {(x1;0),(x2;0),(x3;0,7),(x4;0,4),(x5;0),(x6;0,3)} | {(x1;0,9),(x2;0,7),(x3;1,0),(x4;0,9),(x5;0,5),(x6;0,2)} | |
| {(x1;0,9),(x2;0,8),(x3;0,5),(x4;0),(x5;0),(x6;0,3)} | {(x1;0,7),(x2;1,0),(x3;0,5),(x4;0,2),(x5;0),(x6;0,3)} |
|
|
|
2. По заданным функциям принадлежности нечётких отношений определить максиминную композицию и максмультипликативную композицию согласно варианту.
a) 
| b) 
| c) 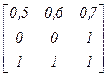
|
d) 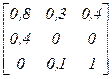
| e) 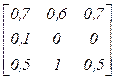
| f) 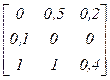
|
| Вариант | 
| 
| Вариант | 
| 
|
| а | e | e | f | ||
| b | а | а | c | ||
| c | b | b | a | ||
| d | c | c | d | ||
| e | d | d | e | ||
| а | f | c | а | ||
| b | f | d | b | ||
| c | e | e | c | ||
| d | а | а | d | ||
| e | b | b | c | ||
| а | d | d | f | ||
| b | e | e | f | ||
| c | d | d | c | ||
| d | b | b | a | ||
| f | c | c | e |
3. Создайте нечёткую экспертную систему в пакете CubiCalc.
Требования к отчету
Отчет о проделанной работе должен содержать:
- название работы, ее задачи и описание последовательности выполнения;
- расчеты согласно пунктам 1 и 2 содержания работы;
- реализацию нечёткой экспертной системы в CubiCalc 2.0.
Контрольные вопросы
1. Что такое нечёткие множества, нечёткие отношения, носитель нечёткого отношения, множество уровня?
2. Сформулируйте правила выполнения операций над нечёткими множествами, отношениями.
3. Перечислите этапы создания проекта в пакете CubiCalc.
ЛАБОРАТОРНАЯ РАБОТА 4
Тема: Решение задач с помощью генетических алгоритмов.
Цель работы: Ознакомиться с подходом к решению оптимизационных задач с помощью генетических алгоритмов (ГА).
Задачи работы:
1. Ознакомиться с основными понятиями ГА.
2. Научиться применять метод ГА для решения задачи о коммивояжере.
3. Изучить программное средство для решения оптимизационных задач с помощью ГА GeneHunter (на примере задачи о коммивояжере).
Теоретические сведения. Основные понятия
Генетический алгоритм (ГА) – это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путем последовательного подбора, комбинирования и вариации искомых параметров. ГА можно рассматривать как одну из разновидностей случайного поиска, которая основана на механизмах, напоминающих естественный отбор и размножение.
ГА начинает работу с некоторого случайного набора исходных решений, который называется популяцией. Каждый элемент из популяции называется хромосомой и представляет некоторое решение проблемы в первом приближении. Хромосомы эволюционируют на протяжении множества итераций, носящих название поколений (или генераций).
Для создания следующего поколения новые хромосомы, называемые отпрысками, формируются либо путем скрещивания двух хромосом-родителей из текущей популяции, либо путем случайного изменения (мутации) одной хромосомы.
Операция скрещивания (кроссовер). Скрещивание является главной генетической операцией. Эта операция выполняется над двумя хромосомами-родителями и создает отпрыск путем комбинирования особенностей обоих родителей. Приведем простейший пример скрещивания – одноточечный (рис.4.1). В начале выберем некоторую случайную точку (точка скрещивания Ts), после этого создадим хромосому-отпрыск (рис. 4.1в) путем комбинирования сегмента первого родителя (рис. 4.1а), стоящего слева от выбранной точки скрещивания, с сегментом второго родителя (рис. 4.1б), стоящего по правую сторону от точки скрещивания.
|
|
|
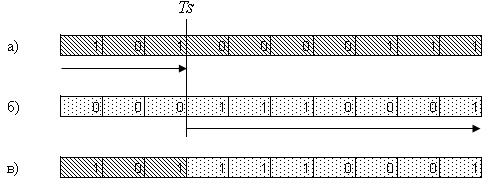
Рис. 4.1– Операция скрещивания
Операция мутации. Мутация – операция, производящая случайное изменение в различных хромосомах. Наипростейший вариант мутации состоит в случайном изменении одной (рис. 4.2) или более хромосом. В ГА мутация играет важную роль для восстановления генов, выпавших из популяции в ходе операции выбора. Интенсивность мутации определяется коэффициентом мутации.

Рис. 4.2 – Операция мутации
Кроме того, используется так называемый оператор инверсии, который заключается в том, что хромосома делится на две части, и затем они меняются местами (рис. 4.3).

Рис. 4.3 – Оператор инверсии
В принципе для функционирования ГА достаточно этих трех генетических операторов, но на практике применяют еще и некоторые дополнительные операторы или модификации представленных операторов. Например, кроссовер может быть не одноточечный, а многоточечный, когда формируется несколько точек разрыва (чаще всего две).
|
|
|


