 |
Программные средства реализации генетических алгоритмов
|
|
|
|
1. MatLab (открытие инструментария ГА осуществляется выполнением команды gatool в командной строке пакета).
2. RawData Analyzer (исследование данных с помощью нескольких видов нейросетей и генетических алгоритмов).
3. NeuroShell GeneHunter (комплекс мощных программных средств для решения оптимизационных задач).
4. Auto2Fit (инструмент, предназначенный для решения оптимизационных задач и проведения сложных инженерных расчетов).
Задача о коммивояжере
Задача коммивояжера является классической оптимизационной задачей, которая формулируется следующим образом: дано множество из п городов и матрица расстояний между ними или стоимостей переезда (в зависимости от интерпретации). Коммивояжеру необходимо объехать все города по кратчайшему пути или с наименьшими затратами на поездку. Причем в каждом городе он должен побывать один раз и вернуться в исходный город.
Для решения предлагается следующая задача: имеется пять телекоммуникационных станций (ТС), стоимость переезда между которыми представлена матрицей (табл. 4.1):
Таблица 4.1– Матрица стоимостей проезда
| ТС | |||||
Решение представим в виде перестановки чисел от 1 до 5, отображающей последовательность посещения ТС; значение целевой функции будет равно стоимости всей поездки, вычисленной в соответствии с вышеприведенной матрицей. Целью решения алгоритма является поиск минимума целевой функции.
Выберем случайным образом два варианта маршрута M и рассчитаем затраты S(M) по каждому из маршрутов:
1) M1=<1,4,2,5,3>, затраты S(M1)=1+1+3+2+3=10;
|
|
|
2) M2=<1,2,3,4,5>, затраты S(M2)=2+1+1+5+4=13.
Маршрут M1 более выгоден, однако он не является самым выгодным из всех возможных.
Разработаны различные модификации операции скрещивания для поиска минимума целевой функции, такие как оператор Грефестета [6, стр.165].
Воспользуемся данным оператором для поиска пути с наименьшими затратами (рис. 4.4).
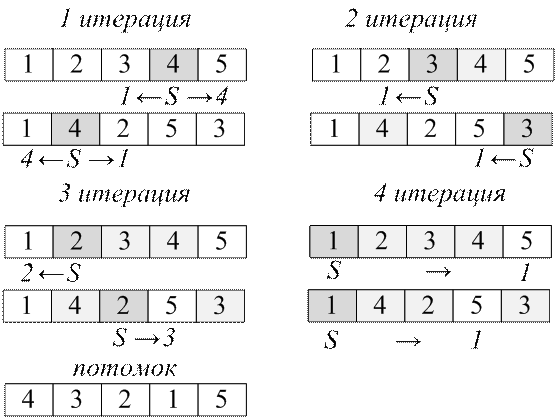
Рис. 4.4 – Иллюстрация работы оператора Грефестета
Таким образом, получили путь M=<4,3,2,1,5>.
Решение задачи о коммивояжере в GeneHunter
Задача о коммивояжере может быть решена с использованием программного средства, например в GeneHunter (рис. 4.5). Коммивояжер должен совершить замкнутый маршрут через заданное количество городов. Все города связаны между собой дорогами, и каждый город коммивояжер должен посетить только один раз. GeneHunter решает эту задачу, выбирая порядок посещения городов и минимизируя длину маршрута.
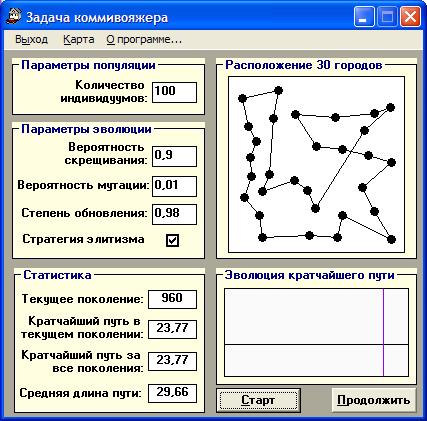
Рис. 4.5 – Решение задачи о коммивояжере в GeneHunter
Здесь задаются следующие параметры:
1. параметры популяции (количество индивидуумов);
2. параметры эволюции:
- вероятность скрещивания pc (случайный способ объединения хромосом из родительской популяции в пары);
- вероятность мутации pm (вероятность изменения значения гена в хромосоме на противоположное);
- степень обновления (обновление исходной популяции путем создания новых особей и уничтожения «бесперспективных», которые не удовлетворяют критерию целевой функции);
- стратегия элитизма заключается в том, что особи с наибольшей приспособленностью гарантировано переходят в новую популяцию.
Содержание работы
1. Решение задачи о коммивояжере методом ГА согласно полученному варианту.
| ТС | ||||||
| 5 + а | 4 + c | 2+b | ||||
| 4 + а | 7+b | 2 + c | ||||
| 4 + b | 8 + а | |||||
| 3 + c | 2 + а | 5+b | ||||
| 1+b | 1 + а | 9 + c | ||||
| 1 + а | 2+b | 5 + c |
|
|
|
2. Необходимо проанализировать работу программы GeneHunter, задав точки городов самостоятельно (карта ® по выбору пользователя); изучить вкладку «Статистика».
| Номер варианта | а | b | c |
Требования к отчету
Отчет о проделанной работе должен содержать:
- название работы, цель, последовательность выполнения;
- решение задачи о коммивояжере в соответствии с полученным вариантом;
- ответы на контрольные вопросы.
Контрольные вопросы
1. Что такое ГА, оператор скрещивания, мутации, инверсии?
2. Поясните цель решения задачи о коммивояжере.
3. Сформулируйте правила, по которым определяется оператор скрещивания Грефенстета.
4. Что такое вероятность скрещивания, мутации, стратегия элитизма?
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Люггер, Дж.Ф. Искусственный интеллект: стратегии и методы решения сложных проблем/ Дж. Ф. Люгер; пер. с англ. под ред. Н.Н.Куссуль.- 4-е изд..- М.: Вильямс, 2003.- 864 с.: ил.
2. Назаров, А. В. Нейросетевые алгоритмы прогнозирования и оптимизации систем/ А. В. Назаров, А. И. Лоскутов; [под ред. М.В. Финкова].- СПб.: Наука и Техника, 2003.- 384 с.: ил.
3. Осовский, С. Нейронные сети для обработки информации/ С. Осовский; пер. с пол. И. Д. Рудинского.- М.: Финансы и статистика, 2004.
4. Пономарев, А.С. Нечёткие множества в задачах автоматизированного управления и принятия решений: Учебное пособие. – Харьков, 2005.
5. Романов, В. П. Интеллектуальные информационные системы в экономике: учеб. пособие для вузов/ В. П. Романов; под общ. ред. Н. П. Тихомирова.- М.: Экзамен, 2003.- 496 с.: ил.
6. Романов, А.Н. Советующие информационные системы в экономике: Учеб. пособие для вузов. / А.Н.Романов, Б.Е.Одинцов. – М.:ЮНИТИ-ДАНА, 2000. – 487 с.
|
|
|
7. Рутковская, Д. Нейронные сети, генетические алгоритмы и нечёткие системы/ Д. Рутковская, М. Пилиньский, Л. Рутковский; пер. с польск. И. Д. Рудинского.- М.: Горячая линия-Телеком, 2004.- 452 с.: ил.
8. Ярушкина, Н. Г. Основы теории нечётких и гибридных систем: учеб. пособие для вузов/ Н. Г. Ярушкина.- М.: Финансы и статистика, 2004.- 320 с.: ил.
9. Яхъяева, Г. Э. Нечёткие множества и нейронные сети: учеб. пособие/ Г.Э.Яхъяева. – М.: Интернет Ун-т Информ. Технологий: БИНОМ. Лаб. знаний, 2006.- 316 с.: ил.
Методические материалы
Жданова Е.И.
Трошин Ю.В.
Халимов Р.Р.
ПРОЕКТИРОВАНИЕ
БАЗ ДАННЫХ И БАЗ ЗНАНИЙ
Методические указания
|
|
|


