 |
Методические указания по решению задач
|
|
|
|
СТАТИСТИКА
Методические рекомендации
по выполнению контрольных работ
Рекомендовано к изданию
Учебно-методическим советом
Оренбургского государственного
Института менеджмента
Оренбург
УДК
ББК
| Г | Горбачева Г. П., Колодина Н. Ф. Статистика: метод. реком. по выполн. контр. работ / Г. П. Горбачева, Н. Ф. Колодина. – Оренбург: Оренб. гос. ин-т менеджмента, 2008. – 65 с. |
| Методические рекомендации содержат общие положения, методические указания по выполнению контрольных работ, а также указания по выбору своего варианта и включены задачи контрольных работ, предоставлен список учебной литературы. Методические рекомендации адресованы студентам заочной формы обучения, обучающимся по специальностям 080507 «Менеджмент организации», 080504 «Государственное и муниципальное управление» |
УДК
ББК
| Горбачева Г. П., Колодина Н. Ф., 2008 | |
| Оренбургский государственный институт менеджмента, 2008 |
Оглавление
| Предисловие………………………………………………………….. | |
| 1 Общие положения…………………………………………………… | |
| 2 Теория статистики…………………………………………………… | |
| 2.1 Методические указания по выполнению контрольной работы. | |
| 2.1.1 Выбор варианта………………………………………………... | |
| 2.1.2 Методические указания по решению задач…………………. | |
| 2.1.3 Задачи контрольной работы…………………………………... | |
| 3. Социально-экономическая статистика……………………………… | |
| 3.1 Методические указания по выполнению контрольной работы. | |
| 3.1.1 Выбор варианта………………………………………………... | |
| 3.1.2 Методические указания по решению задач…………………. | |
| 3.1.3 Варианты контрольных работ………………………………… | |
| Библиографический список |
|
|
|
ПРЕДИСЛОВИЕ
На современном этапе статистическая грамотность – неотъемлемая часть экономического образования. Статистика для специалиста в области экономики – инструмент, позволяющий производить анализ текущей информации и прогнозировать поведение объекта управления. Эффективность управления экономикой в значительной степени зависит от качества информационной базы, основным компонентом которой является статистика. Работая с цифрами, каждый экономист должен знать, как получены те или иные данные, какова их природа, насколько полны они и достоверны. Статистика - самостоятельная отрасль знаний и практической деятельности. Она изучает количественную сторону массовых социально - экономических процессов и явлений в неразрывной связи с их качественной стороной в масштабе экономики страны, отраслей и регионов. Поэтому в системе экономического образования особое место отводится изучению статистики, являющейся базовой научной дисциплиной. В учебной программе статистика объединяет комплекс учебных дисциплин, в составе которого следует выделить такие основные разделы, как «Общая теория статистики» и «Социально-экономическая статистика».
Целью учебной дисциплины «Статистика» является раскрытие содержания системы статистических показателей, отражающих состояние и развитие явлений и процессов общественной жизни.
Предлагаемые вниманию методические рекомендации подготовлены в соответствии с программой курса. В методических рекомендациях по статистике представлены основные требования по выполнению контрольных работ, методические указания по решению задач, варианты контрольных работ и библиографический список
Методические рекомендации подготовлены для студентов 080507.65 «Менеджмент организации», 080504.65 «Государственное и муниципальное управление» заочной формы обучения экономических специальностей. Его использование в изучении курса «Статистика» предполагает всесторонний подход и анализ к рассмотрению каждой отдельной темы, будет способствовать закреплению знаний студентов по пройденному материалу.
|
|
|
ОБЩИЕ ПОЛОЖЕНИЯ
Контрольная работа – одна из форм проверки и оценки усвоенных знаний, получения информации о характере познавательной деятельности, уровня самостоятельности и активности студентов в учебном процессе, эффективности методов, форм и способов учебной деятельности.
Цель контрольной работы:
- изучить важнейшие методы статистики;
- приобрести практические навыки в методологии и расчетах обобщающих статистических показателей, построении и оформлении статистических таблиц и графиков;
- научиться понимать экономический смысл исчисленных показателей, анализировать их и делать практические выводы.
При выполнении контрольной работы необходимо руководствоваться следующими требованиями:
1) задачи выполнять в том порядке, в котором они даны в индивидуальном варианте;
2) записать полностью условие задачи, привести формулы, развернутый расчет с краткими пояснениями и анализом показателей, полученных в результате решения. Если имеется несколько методов расчета того или иного показателя, то применить один из способов, указав при этом и другие возможные;
3) по возможности решение задач следует оформлять в виде таблиц, которые оформляются в соответствии с правилами принятыми в статистике;
4) контрольная работа должна быть выполнена аккуратно, написана разборчиво, не рекомендуется произвольно сокращать слова, допускаются общепринятые сокращения;
5) в конце работы должен быть приведен список использованной литературы.
Контрольные работы, представленные студентом, в которых даны ответы без развернутых расчетов, будут считаться нерешенными. При удовлетворительном выполнении работа оценивается «допущена к собеседованию». К собеседованию студент обязан учесть все замечания рецензента и, не переписывая работу, внести в нее необходимые исправления и дополнения. После успешного собеседования студент получает зачет по работе и допускается к зачету или экзамену. Неудовлетворительные работы выполняются заново в соответствии с замечаниями рецензента.
|
|
|
Если студент не может выполнить контрольную работу или какую-то ее часть, то следует обратиться за консультацией на кафедру финансов, статистики и экономического анализа.
В соответствии с учебным планом студенты заочной формы обучения факультета менеджмента специализаций: «Производственный менеджмент» и «Государственное и муниципальное управление» выполняют письменные контрольные работы по разделам дисциплины «Статистика».
ТЕОРИЯ СТАТИСТИКИ
Методические указания
По выполнению контрольной работы
2.1.1 Выбор варианта
Варианты контрольных работ установлены для студентов с учетом первой буквы фамилии и последней цифрой номера зачетной книжки. Работы, не отвечающие обязательным для студента вариантам, не будут зачитываться.
Таблица 2.1 – Варианты контрольной работы
| Первая буква фамилии | Последняя цифра зачетной книжки | |||||||||
| А Б | 1, 7, 13, 19, 27, 31, | 5, 8, 14, 23, 29, 32, | 3, 9, 14, 22, 28, 33, | 1, 10, 14, 24, 27, 34, | 5, 11, 17, 23, 26, 35, | 3, 12, 14, 19, 30, 36, | 1, 12, 16, 20, 25, 36, | 5, 11, 18, 23, 28, 35, | 3, 10, 15, 23, 29, 34, | 1, 9, 13, 22, 25, 33, |
| В Г | 2, 8, 14, 20, 28, 32, | 6, 7, 13, 22, 30, 34, | 4, 7, 13, 24, 29, 36, | 2, 8, 13, 19, 28, 35, | 6, 9, 18, 22, 25, 31, | 4, 10, 13, 21, 29, 33, | 2, 11, 17, 23, 26, 36, | 6, 12, 15, 24, 27, 35, | 4, 12, 16, 22, 30, 34, | 2, 11, 14, 21, 26, 32, |
| Д Е Ж | 3, 10, 15, 21, 29, 33, | 1, 9, 17, 19, 27, 35, | 5, 8, 18, 23, 30, 35, | 3, 7, 18, 24, 29, 36, | 1, 12, 17, 21, 29, 34, | 5, 11, 17,23, 28, 33, | 3, 10, 18, 22, 27, 35, | 1, 9, 14, 24, 26, 36, | 5, 8, 13, 24, 25, 32, | 3, 7, 16,20, 27, 31, |
| З И К | 4, 10, 16, 22, 30, 33, | 2, 8, 16, 24, 26, 36, | 6, 12, 17, 19, 30, 36, | 4, 10, 17, 23, 30, 31, | 2, 11, 16, 20, 30, 32, | 6, 8, 18, 22, 27, 36, | 4, 9, 15, 21, 30, 36, | 2, 7, 15, 21, 25,35, | 6, 11, 13, 19, 26, 33, | 4, 11, 14, 19, 28, 31, |
| Л М | 5, 11, 17, 23, 29, 34, | 3, 9, 15, 20, 25, 36, | 1, 7, 15, 20, 28, 33, | 5, 11, 16, 22, 25, 32, | 3, 8, 15, 19, 25, 33, | 1, 9, 15, 19, 26, 36, | 5, 10, 14, 20, 25, 34, | 3, 11, 13, 19, 30, 34, | 1, 11, 18, 20, 27, 34, | 5, 12, 13, 24, 29, 32, |
| Н О П | 6, 12, 18, 24, 28, 35, | 4, 10, 14, 19, 30, 35, | 2, 8, 14, 21, 29, 34, | 6, 12, 15, 21, 26, 33, | 4, 9, 14, 19, 26, 34, | 2, 9, 14, 20, 25, 35, | 6, 12, 13, 19, 25, 33, | 4, 11, 16, 20, 29, 33, | 2, 11, 17, 24, 28, 35, | 6, 9, 15, 23, 30, 33, |
| Р С Т | 1, 7, 18, 24, 28, 36, | 5, 11, 13, 21, 29, 34, | 3, 9, 13, 19, 30, 35, | 1, 7, 13, 20, 27, 34, | 5, 7, 13, 20, 27, 35, | 3, 7, 13, 21, 30, 34, | 1, 8, 18, 24, 26, 32, | 5, 9, 17, 23, 28, 36, | 3, 8, 14, 21, 29, 36, | 1, 8, 15, 22, 30, 34, |
| У Ф Х | 2, 8, 17, 23, 27, 36, | 6, 12, 18, 22, 28, 33, | 4, 10, 18, 20, 25, 34, | 2, 8, 14, 19, 28, 35, | 6, 11, 18, 21, 28, 36, | 4, 11, 18, 22, 29, 33, | 2, 9, 16, 19, 27, 31, | 6, 11, 15, 22, 27, 31, | 4, 12, 13, 24, 30, 36, | 2, 7, 15, 21, 29, 35, |
Продолжение таблицы 2.1
|
|
|
| Ц Ч Ш Щ | 3, 9, 16, 22, 26, 35, | 1, 7, 16, 23, 27, 32, | 5, 11, 17, 21, 26, 34, | 3, 9, 15,24, 29, 36, | 1, 12, 16, 22, 29, 33, | 5, 8, 17, 23, 30, 32, | 3, 10, 5, 20, 28, 31, | 1, 10, 18, 23, 26, 32, | 5, 12, 13, 23, 25, 35, | 3, 11, 14, 20, 28, 36, |
| Э Ю Я | 4, 10, 15, 21, 25, 34, | 2, 8, 15, 21, 26, 31, | 6, 12, 16, 22, 27, 36, | 4, 10, 16, 23, 30, 35, | 2, 10, 15, 23, 30, 34, | 6, 11, 16, 24, 28, 31, | 4, 12, 17, 21, 29, 32, | 2, 9, 18, 24, 25, 33, | 6, 8, 18, 22, 26, 34, | 4, 12, 13, 19, 27, 36, |
Методические указания по решению задач
Задачи 1 – 6 составлены по теме «Статистическая сводка и группировка». При решении данных задач предусматривается выполнение аналитической группировки. При этом важно понять суть аналитической группировки, с помощью которой исследуются взаимосвязи изучаемых признаков.
Аналитическая группировка позволяет установить наличие и направление взаимосвязи между факторными и результативными признаками в пределах однородной совокупности. Группировка единиц совокупности производится по факторному признаку. Для составления аналитической группировки требуется определить величину интервала по формуле:
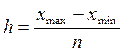, (2.1)
где xmax максимальное значение факторного признака в совокупности,
xmin – минимальное значение факторного признака в совокупности,
n – число групп.
Затем определяется число единиц в каждой из образованных групп, а также объем варьирующих признаков в пределах созданных групп и исчисляются средние размеры результативно показателя (признака) по каждой группе. Результаты группировки оформляются в виде групповой аналитической таблицы.
Аналитическая таблица должна обязательно иметь заглавие, наименование подлежащего и сказуемого, единицы измерения, расчетные и итоговые показатели.
Анализ рядов распределения провести на основе их графического изображения. Для этого нужно построить графики – полигон и гистограмму. Полигон используется при изображении дискретных вариационных рядов. Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Гистограмма применяется для изображения интервального вариационного ряда. Построение интервальных вариационных рядов целесообразно, прежде всего, при непрерывной вариации признака, а также, если дискретная вариация проявляется в широких пределах, т.е. число вариантов прерывного признака достаточно велико. В заключение необходимо дать экономический анализ показателей групповой таблицы и сделать выводы.
|
|
|
Задачи 7 – 12 составлены по теме «Форма выражения статистических показателей». В данных задачах представлены данные, для которых необходимо исчислить относительные показатели.
Относительный показатель – это результат деления одного абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и явлений. При решении задач на относительные показатели основное внимание необходимо уделить обоснованному выбору базы сравнения, определению размерности получаемых величин и их экономической интерпретации. Относительные показатели подразделяются на следующие виды:
Относительный показатель динамики (ОПД):
ОПД = 
. (2.2)
Различают относительные показатели динамики с постоянной и переменной базой сравнения. Если сравнение осуществляется с одним и тем же базисным уровнем, например первым годом рассматриваемого периода, получают относительные показатели динамики с постоянной базой (базисные). При расчете относительных показателей динамики с переменной базой (цепных) сравнение осуществляется с предшествующим уровнем. Рассчитанная величина показывает во сколько раз текущий уровень превышает предшествующий или какую долю от последнего он составляет. Данный показатель может быть выражен кратным отношение или переведен в проценты.
Относительные показатели плана (ОПП) и реализации плана (ОПРП):
ОПП = 
. (2.3)
Данный показатель характеризует напряженность плана, т. е. во сколько раз намечаемый объем производства (или какой-либо финансовый результат деятельности предприятия) превысит достигнутый уровень или сколько процентов от этого уровня составит.
ОПРП = 
. (2.4)
Данный показатель отражает фактический объем производства в процентах или коэффициентах по сравнению с плановым уровнем.
Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого:
ОПС = 
. (2.5)
Выражается в долях единицы или в процентах. Показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге.
Относительный показатель координации (ОПК) представляет соотношение одной части совокупности к другой части этой же совокупности (в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения):
ОПК = 
(2.6)
Показывает во сколько раз данная часть больше базисной, или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу базисной структурной части.
Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
ОПИ = 
(2.7)
Выражается именованной величиной, в процентах, промилле, продецимилле.
Относительный показатель сравнения (ОПСр) представляет собой отношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, районы и т. д.):
ОПСр = 
(2.8)
Выражается в разах.
Задачи 13 – 18 составлены на применение метода средних величин и показателей вариации. В данных задачах представлены интервальные вариационные ряды распределения, для которых необходимо исчислить среднее значение признака, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
В расчетах средней величины следует использовать формулу средней арифметической взвешенной:
. (2.9)
Обозначьте значение осредняемого признака через x, а частоту повторов через f.
Так как в задачах 13 - 15, 17 – 18 значения осредняемого признака представлены в виде интервалов, то необходимо сначала найти их середины, т. е.
, (2.10)
где 
- середина интервалов,
- нижняя граница интервала,
- верхняя граница интервала.
При этом величину первого интервала условно приравниваем к величине второго, величину последнего интервала к величине предпоследнего. Далее произведите расчет средней арифметической.
Расчет дисперсии производится по формуле:
(2.11)
Среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней, т. е. оно исчисляется путем извлечения квадратного корня и измеряется в тех же единицах, что и варьирующий признак. Среднее квадратическое отклонение показывает: на сколько в среднем отклоняются конкретные варианты от его среднего значения. Формула расчета следующая:
. (2.12)
Коэффициент вариации рассчитывается по формуле:
(2.13)
Выражаются в процентах и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Далее ряды распределения изобразить графически и сделать по произведенным расчетам выводы.
Задачи 19 – 24 по теме«Выборочное наблюдение» и предполагают использование формулы для определения необходимого объема выборки. Следует обратить внимание на расчет необходимого объема выборки (п), средней ошибки (
), предельной ошибки выборки (
) для различных видов выборки при повторном и бесповторном отборе.
В задачах 19, 22 – 23 требуется определить границы генеральной средней, которая находится:
, (2.14)
где = t 
.
Значение коэффициента t при различных уровнях вероятности берется из таблицы 2.2.
Таблица 2.2 – Значение коэффициента t при различных уровнях вероятности
| P | 0,683 | 0,950 | 0,954 | 0,997 |
| t | 1,96 |
Таблица 2.3 – Основные формулы видов выборки
| Вид выборки | Необходимый объем выборки при бесповторном отборе | Необходимый объем выборки при повторном отборе | Средняя ошибка при бесповторном отборе | Средняя ошибка при повторном отборе |
| Собственно-случайная | 
| 
| 
| 
|
| Механическая |
| - |
| - |
| Типическая | 
| 
| 
| 
|
| Серийная |  
| 
|  ,
где 
|  ,
где
|
где .
Задачи 25 – 30 составлены на расчет и анализ аналитических показателей динамических рядов, которые определяются по формулам (для удобства и наглядности исходные и рассчитанные показатели изложите в табличной форме, предварительно дав название ей):
Абсолютный прирост (показывает абсолютную скорость роста (снижения) уровня ряда):
базисный 
,
(2.15)
цепной 
,
где 
- порядковый уровень ряда динамики,
- базисный уровень ряда динамики,
-предшествующий уровню ряда динамики.
Темп роста (показывает интенсивность изменения уровней ряда динамики):
базисный 
%,
(2.16)
цепной 
%.
Темп прироста (показывает на сколько процентов возрос или сократился данный уровень ряда динамики по сравнению с базисным или предшествующим):
б азисный 
,
(2.17)
цепной 
%.
Абсолютное значение 1% прироста (расчет этого показателя имеет экономический смысл только на цепной основе):
. (2.18)
Средний уровень ряда динамики (используется для расчета обобщающей характеристики его абсолютных уровней динамики, т. е. для нахождения среднего значения ряда):
. (2.19)
Средний абсолютный прирост (показывает среднегодовой абсолютный прирост ряда динамики) рассчитывается по цепным абсолютным приростам:
, (2.20)
где yn - конечный уровень ряда динамики,
n - число уровней ряда динамики.
Средний темп роста (показывает среднегодовой темп роста - 
) рассчитывается по средней геометрической в рядах динамики по цепным коэффициентам (темпам) роста:
, (2.21)
где m – число коэффициентов роста.
Средний темп прироста вычисляется:
(2.22)
Ожидаемое число того или иного явления исчисляется по среднему темпу роста, когда есть основание считать, что общая тенденция ряда характеризуется экспоненциальной (показательной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции, т.е. по формуле:
, (2.23)
где yi– последний уровень динамики,
t– срок прогноза,
- средний коэффициент роста.
Далее изобразить интенсивность развития ряда динамики графически и сделайте выводы по полученным расчетам.
Задачи 31 – 36 составлены по теме «Индексы». В задачах 31, 34 - 35 следует рассчитать общие индексы, абсолютный размер экономии или перерасхода денежных средств, индекс товарооборота. Необходимо знать методику построения агрегатного индекса, которая предусматривает ответ на три вопроса:
- какая величина будет индексируемой;
-по какому составу разнородных элементов явления необходимо исчислить индекс;
- что будет служить весом при расчете индекса.
При выборе веса следует руководствоваться следующим правилом:
- если строиться индекс количественного показателя (выпуск продукции, объем продажи товаров и др.), то веса берутся за базисный период;
- если строиться индекс качественного показателя (себестоимость, цена, прибыль и др.), то веса берутся за отчетный период.
Так, например:
1) общий индекс физического объема рассчитывается (характеризует изменение количества проданных товаров в физических единицах измерения):
; (2.24)
2) общий индекс цен (характеризует изменение цен):
; (2.25)
3) абсолютный размер экономии или перерасхода денежных средств (разность числителя и знаменателя будет отражать величину экономии (если знак «-» или перерасхода («+»)):
; (2.26)
4) индекс товарооборота (позволяет сравнить товарооборот в текущем периоде с его величиной в базисном периоде):
(2.27)
По расчетам сделать вывод.
Задачи 32 – 33, 36 составлены на расчет индексов переменного, постоянного (фиксированного) состава и индекса структурных сдвигов, измеряющего влияние изменения структуры на динамику среднего показателя. Индекс переменного состава равен соотношению средних уровней изучаемого признака. При изучении динамики средней себестоимости одноименной продукции на двух и более предприятиях, то индекс себестоимости переменного состава исчисляется по формуле:
(2.28)
Выявление влияния факторов на динамику средней себестоимости продукции можно осуществить при помощи расчета индекса себестоимости постоянного состава и индекса структурных сдвигов.
Индекс себестоимости постоянного (фиксированного) состава характеризует изменение средней себестоимости единицы продукции за счет изменения только себестоимости на каждом предприятии:
. (2.29)
Индекс структурных сдвигов характеризует изменение средней себестоимости единицы продукции за счет изменения только удельного веса количества произведенной продукции на отдельных предприятиях. Данный индекс можно исчислить, используя взаимосвязь индексов:
. (2.30)
По расчетам сделать вывод.
Задачи 37 – 42 составлены по теме «Статистическое изучение взаимосвязи социально-экономических явлений».
Задачи 37 – 40 составлены на измерение взаимосвязи между результативными и факторными признаками с помощью парного коэффициента корреляции и коэффициента детерминации.
Для расчета этих коэффициентов существует несколько способов. При решении указанных задач рекомендуется выбрать наиболее простые, а именно, сначала рассчитать парный коэффициент корреляции:
, (2.31)
где r – парный коэффициент корреляции.
| 
| 
|
| 
|
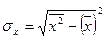
Коэффициент детерминации (r2)вычисляется возведением парного коэффициента в квадрат.
Для нахождения параметров а0 и а1 уравнения регрессии 
следует использовать метод наименьших квадратов. Уравнению прямой соответствует следующая система нормальных уравнений:
(2.32)
где n - объем исследуемой совокупности (число единиц наблюдения).
Для определения параметров а0 и а1 уравнения регрессии , а также парного коэффициента корреляции рекомендуется построить расчетную таблицу.
Таблица 2.4 – Вспомогательная таблица для определения параметров уравнения регрессии
| № п/п | x | y | X2 | Y2 | xy | 
|
Коэффициент эластичности Эx определяется по формуле:
, (2.33)
где 
- среднее значение факторного признака,
- среднее значение результативного признака,
- параметр уравнения при факторном признаке.
Коэффициент эластичности показывает, на сколько процентов в среднем изменяется значение результативного признака при изменении факторного на 1%. По расчетам сделать вывод.
Задача 41 дана на расчет количественной оценки связей социальных явлений. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака.
Таблица 2.5 – Вспомогательная таблица для вычисления коэффициентов ассоциации и контингенции
| а | b | a + b |
| с | d | c + d |
| а + с | b + d | a + b + c + d |
Коэффициенты вычисляются по формулам
ассоциации:
; (2.34)
контингенции:
. (2.35)
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Ка >0,5 или Кк >0,3.
Сделайте краткий вывод.
Задача 42 дана на расчет количественной оценки связей социальных явлений. Каждый из качественных признаков состоит более чем из двух групп и для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова, которые вычисляются по следующим формулам:
, где 
, (2.36)
, (2.37)
где 
- показатель взаимной сопряженности.
, (2.38)
где К1 – число значений (групп) первого признака,
К2 – число значений (групп) второго признака.
Чем ближе величины Кп и Кч к 1, тем связь теснее. Целесообразней построить вспомогательную таблицу для расчета коэффициента взаимной сопряженности. В конце задачи сделать краткий вывод.
Таблица 2.6 – Вспомогательная таблица для расчета коэффициента взаимной сопряженности
| x/y | I | II | III | Всего |
| I II III | … … … | … … … | nxy | nx nx nx |
| Итого | ny | ny | ny | n |
Задачи контрольной работы
Задача 1. Имеются данные по 10 производственным фирмам региона.
Таблица 2.7 – Распределение производственных фирм одного из регионов РФ по стоимости основных фондов и выпуску продукции
| Млн. руб. | ||
| Названия фирм | Стоимость основных фондов | Выпуск продукции |
| Фирма A | ||
| Фирма Б | ||
| Фирма В | ||
| Фирма Г | ||
| Фирма Д | ||
| Фирма Е |
Продолжение таблицы 2.7
| Фирма Ж | ||
| Фирма З | ||
| Фирма К | ||
| Фирма Л |
С целью изучения зависимости между выпуском продукции и стоимостью основных фондов произведите группировку предприятий по стоимости основных фондов, образовав четыре группы с равными интервалами.
По каждой группе и совокупности предприятий в целом подсчитайте:
1) число предприятий;
2) стоимость основных фондов – всего и в среднем на одно предприятие;
3) выпуск продукции всего и в среднем на одно предприятие.
Результаты расчетов представьте в виде групповой таблицы, постройте полигон и сделайте выводы.
Задача 2. Имеются данные по 10 банкам одного из регионов.
Таблица 2.8 – Распределение банков одного из регионов РФ по уставному капиталу и работающим активам
| Млн. руб. | ||
| Названия банков | Уставной капитал | Работающие активы |
| Банк А | 4,7 | 16,6 |
| Банк Б | 5,5 | 6.7 |
| Банк В | 3,6 | 3,9 |
| Банк Г | 11,7 | 17,9 |
| Банк Д | 10,9 | 15,5 |
| Банк Ж | 7,4 | 10,4 |
| Банк З | 3,3 | 12,0 |
| Банк К | 2,7 | 12,8 |
| Банк Л | 4,6 | 6,9 |
| Банк М | 2,9 | 3,2 |
С целью изучения зависимости между размером активов и уставным капиталом произведите группировку банков по размеру уставного капитала, образовав четыре группы с равными интервалами.
По каждой группе и совокупности банков подсчитайте:
1) число банков;
2) размер уставного капитала всего и в среднем на один банк;
3) размер активов всего и в среднем на один банк.
Результаты расчетов представьте в виде групповой таблицы, постройте полигон и сделайте краткие выводы.
Задача 3. Имеются данные за отчетный период о работе негосударственных предприятий отрасли.
Таблица 2.9 – Распределение негосударственных предприятий по выпуску продукции и суммам затрат на производство продукции одной из отрасли экономики
| Тыс. руб. | ||
| Негосударственные предприятия | Выпуск продукции | Сумма затрат на производство продукции |
| Предприятие А | 2,0 | |
| Предприятие Б | 5,5 | |
| Предприятие В | 3,6 | |
| Предприятие Г | 15,7 | |
| Предприятие Д | 10,9 | |
| Предприятие Ж | 17,4 | |
| Предприятие З | 3,3 | |
| Предприятие К | 2,7 | |
| Предприятие Л | 4,6 | |
| Предприятие М | 4,9 |
Для изучения зависимости между затратами на производство продукции и объемом выпуска продукции произведите группировку предприятий по объему выпуска продукции, образовав четыре группы с равными интервалами.
По каждой группе и по совокупности предприятий в целом подсчитайте:
1) число предприятий;
2) выпуск пр
|
|
|
