Достаточные условия оптимальности

Методы нелинейной оптимизации

Задача математического программирования

(1)     (2)

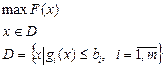
называется задачей нелинейного программирования, если функция цели или хотя бы одна из функций ограничений не линейна.

Точка 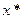называется точкой локального экстремума, если существует 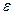– окрестность этой точки 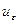, для которой , .

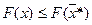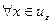Точка 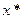называется точкой глобального максимума, если для любого .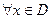

Точка 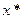называется точкой глобального минимума, если для любого .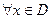

 

Функция называется унимодальной (одноэкстремальной), если у этой функции имеется только один локальный экстремум. В противном случае она называется многоэкстремальной.

В классической теории оптимизации рассматриваются экстремальные задачи без ограничений, то есть область D совпадает со всем n -мерным пространством вещественных чисел .

 

Классическая теория оптимизации (Должны быть изучить в курсе ВМ)

 

Рассмотрим задачу безусловной оптимизации

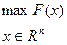
В случае достаточной дифференцируемости функции можно сформулировать необходимые и достаточные условия локального экстремума.

 

(3)

7.1. Необходимые условия оптимальности

 

Для функции одной переменной справедлива следующая теорема.

 

Теорема 1: для того, чтобы функция одной переменной имела в точке 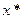локальный экстремум, необходимо, чтобы производная функции в этой точке была равна нулю.

 

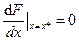
Аналогичная теорема справедлива для функции многих переменных.

Теорема 2: для того, чтобы функция 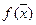имела в точке 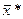локальный экстремум, необходимо, чтобы все ее частные производные в этой точке обращались в ноль

(4)

Другими словами, вектор градиента функции в этой точке должен быть нулевым.

(5)

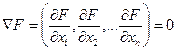
Такие точки называются стационарными точками функции.

 

Достаточные условия оптимальности

Для функции одной переменной достаточные условия задаются следующей теоремой.

Теорема 3: если в точке 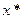первая производная функции равна нулю 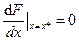, а вторая производная 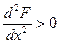, то функция в точке 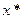имеет локальный минимум, если 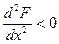, то функция в точке 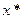имеет локальный максимум.

Если вторая производная функции в точке 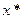равна нулю, то необходимо исследовать производные высших порядков в соответствии со следующей теоремой.

 

Теорема 4: если функция одной переменной имеет в точке 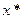производные до 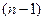порядка равными нулю и производная 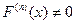, то тогда,

если 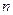четно, то точка 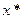является точкой минимума, если ,

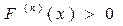точкой максимума – если .

Если 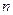нечетно, то точка 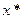– точка перегиба.

 

Для обобщения теоремы 3 на случай функции многих переменных рассмотрим матрицу вторых производных функции и её свойства.

Матрицей Гессе (Гессианом) называется матрица вторых производных функции:

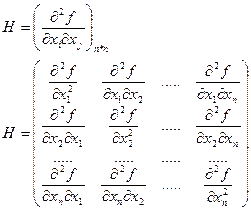
Для анализа поведения функции в точке потребуются некоторые свойства квадратичных функций.

Рассмотрим квадратичную функцию (форму):

(6)

Числовая матрица 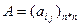называется матрицей квадратичной формы. Можно считать, что эта матрица симметрична.

Квадратичная форма (6) называется положительно определенной, если для 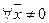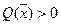и отрицательно определенной, если для .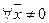

Симметричная матрица A называется положительно определенной, если построенная по ней квадратичная форма (6) положительно определена.

Симметричная матрица 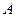называется отрицательно определенной, если построенная по ней квадратичная форма (6) отрицательно определена.

Проверить положительную или отрицательную определенность числовой матрицы можно по следующим признакам.

Признаки:

1. Критерий Сильвестра: матрица 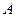является положительно определенной, если все ее угловные миноры больше ноля.

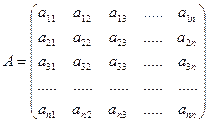
Матрица 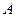является отрицательно определенной, если знаки угловых миноров чередуются.

Или: если все угловые миноры удовлетворяют неравенству .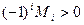

2. Для того чтобы матрица была положительно определенной, необходимо, чтобы все ее собственные числа были больше нуля.

Собственные числа – корни многочлена . Этот определитель есть многочлен относительно .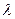

.

Для того чтобы матрица была отрицательно определенной, необходимо, чтобы все ее собственные числа были меньше нуля.

 

Достаточное условие оптимальности задается следующей теоремой.

Теорема 5: если в стационарной точк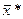е (т.е. ) матрица Гессе положительно определена, то эта точка – точка локального минимума, если матрица Гессе отрицательно определена, то эта точка – точка локального максимума.

Доказательство:

Пусть 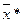– стационарная точка, , возьмем окрестность точки 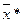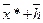. Тогда по теореме Тейлора

(7)

По условию теоремы , а матрица Гессе в точке 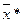положительно определена, то есть квадратичная форма >0 в точке 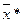, а в силу непрерывности вторых частных производных и в точке .

Значит точка 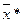– точка локального минимума.

 

Пример Решения задачи на безусловный максимум.

Пример: Продукция трех видов производится в объеме и реализуется по цене 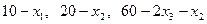соответственно. Определить объемы производства, обеспечивающие наибольший доход.

Определим стационарные точки функции

:

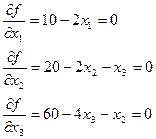
Решением этой системы линейных алгебраических уравнений является вектор

Проверим достаточное условие оптимальности. Вычислим матрицу Гессе в полученной стационарной точке.

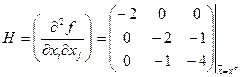
Угловые миноры матрицы имеют чередующиеся знаки

,
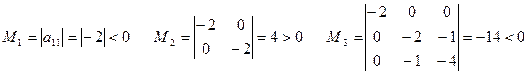значит, матрица Гессе отрицательно определена и точка – точка локального максимума. При полученных объемах производства будет достигнут наибольший доход .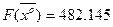

 

Проверим отрицательную определенность матрицы вторым способом. Найдем собственные числа матрицы Гессе

Так как все собственные числа матрицы 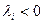, то матрица отрицательно определена и – локальный максимум.

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: