 |
Метод приведенного градиента
|
|
|
|
Основная идея градиентных методов.
Наибольшее распространение получили методы возможных направлений.
Рис.(э.3).
В исходной точке Х 0 рассматривается несколько направлений (рис. э.3) для перехода в новую точку Х 1. Возможными называют направления, которые ведут в сторону уменьшения целевой функции (направления 1 и 4). Перемещение допускается по любому возможному направлению 
в текущей точке пропорционально некоторой константе t, называемой шагом, т.е.
. (3.5)
В точке Х 1 аналогично выбирается возможное направление и делается очередной шаг. Общее уравнение итерационного процесса по методу возможных направлений
. (3.6)
Величина шага влияет на сходимость вычислительного процесса, определяемую числом итераций: при малых t – процесс сходится, но медленно; при больших t – процесс может расходиться.
Между этими крайностями существует оптимальный шаг, который на принятом направлении приводит в точку максимального значения F, где это направление касается линии 
(рис. э.4)
Рис.э.4
Для отыскания оптимального шага 
можно на принятом направлении выражение 
подставить в целевую функцию 
и после преобразований получить новую функцию, зависящую только от шага 
, а затем найти ее минимальное значение.
В математике известно правило определения производных с учетом неявновыраженных функций.
Запишем исходную задачу с учётом разделения исходного вектора неизвестных на составляющие 
и 
:
(3.29)
Запишем производную 
с учетом неявной зависимости 
, (3.30)
где производные в скобках определяются с учетом явной зависимости 
от и .
Производную 
найдем из ограничения 
, которое в результате дифференцирования определяет условие
, (3.31)
|
|
|
позволяющее получить
(3.32)
Здесь 
– квадратная матрица (
), для которой существует обратная 
.
После подстановки (3.32) в (3.30) получим
.
Полученный градиент 
, составляющие которого определяются независимыми переменными, и называется приведённым градиентом.
Этот градиент может использоваться в процедуре градиентного метода:
(3.34)
Геометрически приведённый градиент является проекцией градиента 
на поверхность ограничений, а точнее – на плоскость, касательную нелинейной поверхности в текущей точке (рис. 3.17).
Рис.э.3
В точке условного минимума функции равен 0.
Решим пример 1.
Воспользуемся формулой (3.33) для приведенного градиента
В качестве свободной переменной примем 
. Тогда зависимой будет 
, и пользуясь (*.3) получаем 
.
В решаемой задаче х1 является составляющей , а относится к . С учетом этого
.
| (*.9) |
|
С учетом этого приведенный градиент
|
Основное уравнение градиентного метода
| |
|
Рис.э.4
Решим пример1, взяв в качестве точности вычислений ε равное 0,01. В качестве исходного приближения примем
 =0 
|
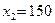
Все расчеты приведены на рис. рис.э.5-э.10. Приближенные значения 
и 
содержатся в интервале ячеек В3:С13. Значения приведенного градиента 
содержатся в интервале ячеек D3:D13. Шаг (величина) изменения равная 
содержатся в интервале ячеек F3:F13. Значения целевой функции – величины дохода записаны в интервале ячеек G3:G13. Модуль приведенного градиента 
с каждым шагом уменьшается от 420 в стартовый момент, до 0.04 на 10 шаге (рис.э.6), что свидетельствует о правильном движении найденных приближений в сторону экстремума функции.. Таблица содержит 11 строк (
=0,1,2,..10), поскольку на 10 шаге модуль приведенного градиент стал равен 0.04, что меньше заданной точности вычислений ε (0.01). Приближенные значения 
=69.9927 
=80.0073 содержатся в ячейках В13 и С13 соответственно. Отличие от решения, полученного аналитическими методами, составило менее 0,01. Обратите внимание, как происходит стабилизация значений 
, и 
с ростом , т.е. значения в соседних строках отличаются все меньше и меньше. Этот факт также проиллюстрирован графиком на рис.э.7.
|
|
|
Рис.э.5
Рис.э.6
Рис.э.7
Рис.э. 8
|
|
|
