 |
Листинг 6.2. Фрагмент программы. Предельное число итераций NIterMax и точность eps должны быть заданы.
|
|
|
|
Методические указания по выполнению домашних заданий для студентов 1 курса специальности ИУ-10.
Оглавление.
Введение. 1
Домашнее задание 1. 1
Практикум 6. Приближенные вычисления. 1
Задача 6.1. 3
Задания. 5
Задача 6.2. 7
Задания. 9
Практикум 7. Процедурные типы. 11
Задача 7.1. 13
Задания. 16
Задача 7.2. 17
Задания. 20
Домашнее задание 2. 21
Практикум 13. Типизированные файлы. 21
Задача 13.1. 21
Задания. 30
Домашнее задание 3. 35
Практикум 18. Использование объектной технологии для построения движущихся фигур. 35
Введение.
Поскольку домашние задания являются составной частью курса, то в настоящем пособии сохранена нумерация разделов, соответствующих темам домашнего задания из «Практикума по программированию», издание которого готовится в настоящее время на кафедре ИУ-10.
Домашнее задание 1.
Практикум 6. Приближенные вычисления.
Все приближенные вычисления выполняются над данными действительного типа, обычно real или double. Для приближенных методов вычисления, как правило, строится итерационный цикл по точности. Итерацией будем называть однократное выполнение этого цикла. Из трех конструкций цикла чаще всего используются циклы
repeat <операторы> until<условие окончания>;
while<условие продолжения> do <оператор>;
Цикл for...to… do … используется крайне редко, поскольку заранее никогда не известно на какой итерации будет достигнута заданная точность. Понятие точности решения мы будем использовать самое очевидное, не вдаваясь в математические тонкости, что, впрочем, не означает их отрицание. Наконец, кроме точности будем использовать дополнительно ограничение числа итераций.
Решение нелинейных алгебраических уравнений.
|
|
|
В дальнейшем будем считать, что на интервале x Î [a, b] существует корень уравнения f(x)=0 и этот корень единственный (рис.6.1). Сущность всех методов численного решения нелинейных алгебраических уравнений заключается в поиске такой точки c внутри интервала [a, b] ( т.е. с Î [a, b]), чтобы эта точка делила [a, b] на две части [a, с] и [с, b].
Не имеет принципиального значения способ определения точки c. Если координаты точки определяются как среднее арифметическое [a, b], то этот метод называется методом половинного деления. Если эта точка является точкой пересечения оси абсцисс и хорды AB, то это метод хорд.
Корень уравнения x0 находится теперь на одном из двух интервалов – либо на [a, с], либо на [с, b]. Если корень на [a, с], то полагается b=с, в противном случае для интервала [с, b] полагается a=с. Далее вычисления повторяются, пока не будет достигнута заданная точность.
Признаком того, что корень находится на [a, с] является выполнение неравенства f(a)*f(с)<0, в противном случае корень будет находится на втором интервале.

Рис.6.1. Методы определения приближенного положения корня.
Задача 6.1.
Найти все корни нелинейного уравнения x2-sin(x)=0 методом половинного деления с точностью 0.0001.
Этап 1. В этой и подобных задачах полезно вначале построить график функции вида y(x)=x2-sin(x), чтобы приближенно локализовать положение корней на оси абсцисс и подсчитать их количество. Элементарный анализ показывает, что это уравнение имеет тривиальный корень в точке x=0 и еще один корень на интервале от 0 до p/2. Отрицательных корней у этого уравнения нет. Таким образом, задача сводится к нахождению единственного корня. Левая граница интервала представляет собой число близкое к нулю, например 0.001. В качестве правой границы достаточно ограничится значением 1.0, поскольку при больших значениях функция x2 выходит из области допустимых значений функции sin(x).
|
|
|
Этап 2. На этом этапе, прежде всего, программируется заданная функция y(x), а затем в основной программе реализуется алгоритм нахождения корня. Ниже представлен листинг программы, в котором итерационный цикл по точности построен с помощью оператора цикла с постусловием. Начальные значения границ интервала, требуемая точность и максимальное число итераций заданы константами.
Листинг 6.1. Алгоритм нахождения корня нелинейного уравнения методом половинного деления (заголовок программы не приводится).
Function y(x: real):real;
Begin result:=x*x-sin(x); End;
Var a, b, c: real;
iter: longword;
BEGIN
a:=0.001; b:=1.0; iter:=0;
Repeat
c:=0.5*(a+b);
if y(a)*y(c)<0 then b:=c else a:=c;
if abs(y(c))<0.0001 then break;
inc(iter);
until iter>1000;
writeln(' iter=', iter);
writeln(' c=',c:7:5,' y(c)=', y(c):7:5);
readln;
END.
Этап 3. Самостоятельная работа. Представленный выше алгоритм является достаточно сырым для практического использования, поэтому следует оформить его в виде функций с интерфейсом для метода половинного деления и метода хорд[1] соответственно
Function Xd(a, b: real; eps: real): real;
Function Xh(a, b: real; eps: real): real;
где Xd – приближенное значение корня в методе половинного деления, Xh – приближенное значение корня в методе хорд; a, b – диапазон поиска ;eps – точность. Условием прекращения итераций считать выполнение неравенства abs(b-a)<eps или превышение заданного числа итераций (задать константой const iterMax=1000;).
Задания.
С использованием функций Xd и Xh составить программу нахождения всех корней нелинейного уравнения y(x)=0 в заданном интервале методом половинного деления и методом хорд с точностью eps=0.0001. Вывести значение корня и значение функции при данном корне.
Указание. Уравнение может иметь несколько корней в заданном интервале, поэтому для правильного определения количества корней и локализации диапазона поиска корня a,b целесообразно вначале построить график функции y(x). Поиск корней сразу на всем интервале обычно приводит к ошибочным результатам.
Вариант Функция y(x) Интервал
1. y(x)= sin(2*x)-0.2*x; [0; 5]
2. y(x)= cos(2*x)-0.2*x; [0; 5]
3. y(x)= sin(x)-(4-0.5*(x*x-2)); [-5; 5]
4. y(x)= cos(x)-(4-0.5*(x*x-2)); [-5; 5]
5. y(x)= 7.37*cos(x)-1/x; [0.1; 2]
6. y(x)= 3.37*sin(x)-1/x; [0.2; 2]
7. y(x)= sin(x)-(((x-1)*x+1)*x-1); [-2; 2]
8. y(x)= cos(x)-(((x-1)*x+1)*x-1); [-2; 2]
9. y(x)= exp(-sqr(x-4))-0.2*x; [2; 5]
10. y(x)= exp(-sqr(x-4))-cos(x); [4; 12]
11. y(x)= exp(-sqr(x-4))-sin(x); [0; 5]
12. y(x)= 5*exp(-sqr(x-4))-(arctan(x-3)+2); [0; 5]
|
|
|
13. y(x)= 2.73*sin(x)-(arctan(x-3)+2); [0; 5]
14. y(x)= x-0.5*x*x-arctan(x-3); [-5; 5]
15. y(x)= 0.2*x - sin(2*x); [0; 5]
16. y(x)= 0.2*x - cos(2*x); [0; 5]
17. y(x)= 4-0.5*(x*x-2) - sin(x); [-5; 5]
18. y(x)= 4-0.5*(x*x-2) - cos(x); [-5; 5]
19. y(x)= 1/x - 7.33*cos(x); [0.1; 2]
20. y(x)= 1/x - 3.37*sin(x); [0.2; 2]
21. y(x)= (((x-1)*x+1)*x-1) - sin(x); [-2; 2]
22. y(x)= (((x-1)*x+1)*x-1) - cos(x); [-2; 2]
23. y(x)= 0.2*x - exp(-sqr(x-4)); [2; 5]
24. y(x)= cos(x)- exp(-sqr(x-4)); [4; 12]
25. y(x)= sin(x)- exp(-sqr(x-4)); [0; 5]
26. y(x)= arctan(x-3)+2 - 5*exp(-sqr(x-4)); [0; 5]
27. y(x)= arctan(x-3)+2 - 2.73*sin(x); [0; 5]
28. y(x)= arctan(x-3)-(x-0.5*x*x); [-5; 5]
Вычисление суммы степенного ряда.
Математические основы и алгоритм решения этой задачи подробно рассмотрены в учебно-методическом пособии [2], поэтому ниже приведены лишь основные моменты.
Из курса математики известно, что любую функцию f(x), имеющую в окрестности точки x0 бесконечное число производных, можно разложить в окрестности этой точки в бесконечный степенной ряд с любой, наперед заданной точностью. Аналитическое выражение такого ряда называется формулой Тейлора. В частном случае, при x0=0, формула Тейлора называется также формулой Маклорена (MacLaurin).
f(x)=f(0)+f’(0)*x/1!+f”(0)*x2/2!+…f(n)(0)*xn/n!+…
Естественно, количество членов ряда, удерживаемых при разложении, будет зависеть от точности. Иначе говоря, точность нужна для определения количества членов ряда при разложении. Во избежание путаницы, всегда будем нумеровать члены ряда, содержащие члены с xn/n! натуральными числами 1, 2, 3…, а члену f(0) присвоим номер 0, т.е.
f(x)=a0+a1+a2+a3…an-1+an+an+1+…
Нетрудно заметить, что у таких рядов отношение rn=an+1/an, не содержит функции факториала и достаточно легко может быть вычислено. Таким образом, если известен текущий член ряда an и имеется формула, позволяющая определить rn, то следующий член ряда может быть найден по рекуррентной формуле an+1=rn * an. Первый член рядавсегда известен, по нему можно найти второй, по второму третий и т.д. Осталось все это просуммировать и добавить a0.
Из теории степенных рядов известны несколько оценок точности. Мы будем пользоваться следующей оценкой: точность считается достигнутой при выполнении условия |an+1 |<eps, где eps наперед заданное малое число.
Таким образом, алгоритм программирования ряда включает в себя «бумажный» этап и собственно программирование. От того насколько успешно, а главное ясно и понятно выполнены выкладки на бумаге, зависит конечный результат.
|
|
|
Задача 6.2.
Составить программу вычисления ряда, получающегося при разложении функции f(x)=sin(x) в окрестности точки x=0.
f(x)=x-x3/3!+x5/5!-x7/7!+…
Этап 1. «Бумажный». Выполняется с особой тщательностью без компьютера.
1. Отделяются все члены ряда слева, относительно которых есть хоть малейшие сомнения в их принадлежности к ряду. У первого члена нет факториала – уже повод для сомнения, отделяем. Здесь принцип «маслом кашу не испортишь». Эти отделяемые члены группируются в слагаемое a0=x.
2. Оставшиеся члены нумеруются натуральными числами 1, 2, 3…
f(x)=x - x3/3! + x5/5! - x7/7!+…
n -> 1 2 3 …
3. Подбором находится формула для n –го члена ряда. В нашем случае
an=(-1)nx2*n+1/(2*n+1)!
Полученную формулу следует обязательно проверить на двух – трех членах ряда.
4. Самое трудное действие – определение знаменателя ряда. В числитель подставляется формула для n+1 -го члена ряда, а в знаменатель – для n –го члена ряда.
rn=an+1/an=[ (-1)n+1x2*n+3/(2*n+3)!] / [ (-1)nx2*n+1/(2*n+1)!]
После сокращения степеней остаются факториалы
rn=-x2(2*n+1)!/(2*n+3)!
Чтобы упростить это выражение, необходимо больший факториал выразить через меньший. По определению факториала, путем записи в «обратную» сторону
(2*n+3)!=(2*n+3) (2*n+2)[ (2*n+1) (2*n+0) (2*n-1)…]
Сомножители в квадратных скобках есть ни что иное, как меньший факториал (2*n+1)!. Итак, окончательно (обратите внимание на общие скобки знаменателя)
rn=-x2/((2*n+3)*(2*n+2)).
Все! Можно включать компьютер.
Этап 2. Использование рекуррентной формулы предполагает, что существует некоторое начальное состояние ряда, от которого и будут «развиваться события». Естественно выбрать в качестве такого состояния, ряд при n=1, в котором есть только два слагаемых a0 и an= -x3/6, а его сумма равна s=a0 + an. Все дальнейшие действия выполняются в итерационном цикле по точности. Для заданного n вычисляется знаменатель ряда rn, затем по рекуррентной формуле определяется следующий член ряда an+1, накапливается новая сумма членов ряда и n увеличивается на единицу. Фрагмент программы, реализующий этот алгоритм, представлен на листинге ниже.
Листинг 6.2. Фрагмент программы. Предельное число итераций NIterMax и точность eps должны быть заданы.
iter:=0; // Счетчик итераций
x:=0.5*3.14159; // Аргумент (параметр)
n:=1; a0:=x; an:=-x*x*x/6; s:=a0+an; // Настройка
Repeat
r:=-x*x/((2*n+3)*(2*n+2));
an:=r*an; s:=s+an;
inc(n); inc(iter);
if abs(an)<eps then break;
until iter>NIterMax;
writeln(' iter=', iter);
writeln(' s=', s:7:5);
Этап 3. Самостоятельная работа. Представленный выше алгоритм является лишь заготовкой. Его необходимо оформить в виде функции с интерфейсом
|
|
|
Function R(x: real; eps: real): real;
где R сумма членов ряда, вычисленная при аргументе x с точностью eps.
Задания.
С использованием функции, оформленной в соответствии с требованиями этапа 3 предыдущей задачи, составить программу вычисления суммы членов ряда с точностью 0.0001 для своего варианта задания.
1. 
2. 
3. 
4. 
5. 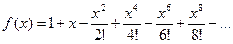
6. 
7. 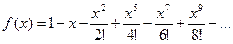
8. 
9. 
10. 
11. 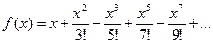
12. 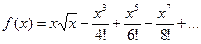
13. 
14. 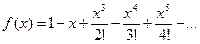
15. 
16. 
17. 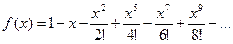
18. 
19. 
20. 
21. 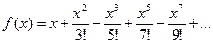
22. 
23. 
24. 
25. 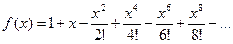
26. 
27. 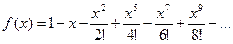
28. 
29. 
30. 
31. 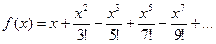
32. 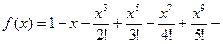
|
|
|


