 |
Практикум 7. Процедурные типы.
|
|
|
|
Основной целью этого практикума является изучение процедурных типов, но задачи практикума относятся к теме приближенных вычислений и фактически продолжают материал предыдущего практикума.
Вычисление площади под кривой по методу Дарбу – Римана.
Математические основы и алгоритм решения этой задачи подробно приведены в учебно-методическом пособии [3], поэтому ниже рассмотрены лишь основные моменты. Метод получил свое название по имени известных математиков впервые предложивших его.
Пусть на интервале [a..b] определена непрерывная положительная и монотонная функция Y=f(x), как это показано на рис. 7.1. При разбиении интервала на n равных отрезков шириной dx площадь под кривой, заданной этой функцией, можно аппроксимировать суммой площадей n прямоугольников с основанием dx двояким образом. Если в качестве высоты прямоугольника выбрать меньшую ординату f(x), соответствующую правой границе отрезка, то очевидно, что такая аппроксимация даст значение искомой площади с недостатком S1, а сама площадь получила название нижней площади Дарбу. При выборе в качестве высоты большей ординаты f(x+dx), соответствующей левой границе отрезка, аппроксимация получила название верхней площади Дарбу и даст значение искомой площади с избытком S2.
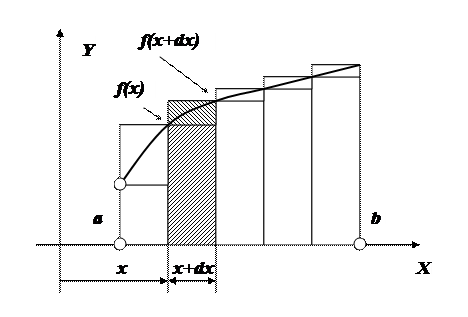
Рис. 7.1. Площади Дарбу. Прямоугольники s1=dx*f(x) – «малые», s2=dx*f(x+dx) – «большие». Сумма площадей всех «малых» прямоугольников S1=Ss1 – дают нижнюю площадь Дарбу, а всех «больших» S2=Ss2 – верхнюю площадь Дарбу.
Риман показал, что точное значение искомой площади S находится между S1 и S2 и, что самое главное, существует предел | S1 - S2 | < eps(dx), где eps(dx) - сколь угодно малое число, зависящее от dx. Именно эта оценка точности и будет использоваться для приближенного вычисления площади под кривой. Наконец, поскольку в методе Дарбу-Римана рассматриваются только неотрицательные функции, площадь под кривой, по своему геометрическому смыслу, не следует полностью отождествлять с определенным интегралом.
|
|
|
При программировании данной задачи необходимо учитывать, что на участке, где функция монотонно убывает, формулы для расчета площади «больших» и «малых» прямоугольников должны быть инвертированы, т.е. s1=dx*f(x+dx), s2=dx*f(x).
Задача 7.1.
Составить программу вычисления площади под кривой, заданной функцией f(x)=sin(x) на интервале x =[0..p] с точностью eps=0.0001.
Этап 1. Отладку алгоритма следует начать с основного цикла суммирования при заданном числе разбиений. После этого этапа, можно переходить к отладке внешнего цикла подбора числа разбиений для достижения требуемой точности.
Таким образом, функционально к циклу суммирования будем относить подготовительную часть и собственно цикл. Причем, поскольку число разбиений считается известным, то проще всего использовать оператор цикла «for».
Ниже приведен фрагмент программы вычисления площади под кривой y=sin(x) в диапазоне от 0 до p, при числе разбиений n, равном 100.
Листинг 7.1а. Цикл суммирования при заданном числе разбиений. Функциональная часть цикла выделена курсивом.
// Заданная функция определена в разделе P&F
Function y(x: real): real;
Begin result:=sin(x); End;
// Глобальные параметры и основная программа
Var a, b, x, dx, y1, y2, s1, s2: real;
n, i: word;
BEGIN
a:=0; b:=Pi; n:=100;
// Начало цикла суммирования
dx:=(b-a)/n; s1:=0; s2:=0;
for i:=1 to n do
Begin
x:=a+dx*(i-1);
y1:=y(x);
y2:=y(x+dx);
if y2>y1
Then // Функция возрастает
begin s1:=s1+dx*y1;
s2:=s2+dx*y2; end
Else // Функция не возрастает или убывает
begin s2:=s2+dx*y1;
s1:=s1+dx*y2; end;
end;
// Окончание цикла суммирования
Writeln(s1:7:4, s2:7:4); // 1.9684 2.0313
readln;
END.
Этап 2. После отладки программы с циклом суммирования при заданном числе разбиений, можно переходить к программированию внешнего цикла по точности. В приведенном ниже листинге текст цикла суммирования опущен. Функциональную часть цикла, которая на листинге выше выделена курсивом, необходимо вставить в указанное место. Управление точностью производится за счет увеличения числа разбиений в два раза за одну итерацию. Как и в предыдущих программах, выход из цикла при достижении заданной точности eps производится с помощью процедуры break, а условием прекращения цикла является превышение максимального числа итераций NIterMax. Обратите внимание на замену типа целочисленных переменных с word на longword, поскольку число разбиений n может быть очень большим.
|
|
|
Листинг 7.1б. Цикл по точности. Заголовок программы и раздел описаний P&F с функцией y(x) не приводятся.
Const NIterMax=10000;
eps=0.0001;
Var a, b, x, dx, y1, y2, s1, s2: real;
n, i, iter: longword;
BEGIN
a:=0; b:=Pi;
n:=10; iter:=0;
Repeat
// Текст цикла суммирования из листинга 7.1а
if abs(s1-s2)<eps then break;
n:=2*n; // Увеличение числа разбиений
inc(iter);
until iter > NIterMax;
Writeln(s1:9:5, s2:9:5); // 1.99996 2.00004
writeln(' iter=', iter); // 13
readln;
END.
Задания.
1. Преобразовать алгоритм вычисления площади под кривой в функцию, возвращающую значение 0.5*(s1+s2) с интерфейсом
Function Sq(a,b,eps:real; Var s1, s2:real):real;
Значения s1, s2 являются выходными и возвращаются через список параметров. Диапазон a,b и точность eps являются входными параметрами.
2. С использованием функции Sq составить программу вычисления площади под кривой y=abs(f(x)) с точностью eps=0.001. Функцию f(x) и значения a,b взять для своего варианта в задании к первой части Практикума 6 «Решение нелинейных алгебраических уравнений». Вывести значения площади и отдельно площадей s1 и s2. Вывод результатов выполнять только в основной программе. При необходимости можно использовать вывод диагностических сообщений из процедур и функций.
Процедурные типы.
После того, как предыдущее задание будет выполнено, у тех, кто это сделал самостоятельно, возникнет вполне законный вопрос №1, а у тех, кто этого не сделал – вполне понятное желание №2.
Между тем, получение ответа на вопрос №1 и есть предпосылка для выполнения желания №2.
Итак, вопрос №1. Можно смириться с тем, что для вычисления площади под кривой, заданной другой функцией, например для другого варианта, требуется переписать исходный код глобальной функции y(x). Но, что же делать, если необходимо в одной программе вычислить, площади для нескольких функций? Можно, конечно, создать несколько копий-аналогов функции Sq, отличающихся только именами и используемой глобальной функцией, но тогда желание №2 покажется уж вовсе недостижимым. Для решения этой и подобных проблем в DELPHI существует механизм передачи в функцию вычисления площади любой другой функции, без ее перепрограммирования, получивший название процедурные типы.
|
|
|
Все программные единицы, будь то основная программа, процедура или функция, «живут» в линейной памяти компьютера примерно одинаково: есть область программного кода со своим адресом и есть область данных со своим. Иначе говоря, если мы знаем где, по какому адресу, находится программный код, и знаем где и как устроены данные, т.е. знаем, сколько их, знаем их типы, то этого достаточно.
Таким образом, чтобы передать подпрограмме другую подпрограмму (процедуру или функцию) достаточно сообщить ей две сущности
• Адрес начала программного кода.
• Шаблон, по которому «скроен» список параметров, т.е. их количество и типы.
Создатели DELPHI сознательно решили скрыть всю эту адресную подоплеку, заменив ее понятием процедурного типа.
Задача 7.2.
Составить функцию вычисления площади под кривой для произвольной функции с двумя аргументами действительного типа. С использованием этой функции составить программу вычисления площади под двумя кривыми вида y=abs(f(x)) с точностью 0.001. Первая кривая f(x) является аналитической функцией и соответствует условиям задачи 6.1, а вторая представлена в виде ряда с условиями задачи 6.2.
Этап 1. Планирование структуры программы. На этом этапе следует объявить соответствующий процедурный тип и распределить местоположение программных составляющих хотя бы в виде комментариев[2]. В качестве первого параметра процедурного типа указан аргумент x, а вторым параметром является точность e, которая используется только при вычислении ряда. При передаче через процедурный тип аналитической функции значение второго параметра может быть любым.
|
|
|
|
|
|


