 |
В массиве грунта от действия полосовой нагрузки
|
|
|
|
Построить эпюры вертикальных сжимающих напряжений в массиве грунта от действия полосовой нагрузки р, изменяющейся по закону прямой в точках на заданной вертикали и горизонтали, расположенной на расстоянии z от поверхности (рис. 4.1). Точки по вертикали на глубине 0, 1, 2, 4 и 6 м, по горизонтали на границах и в середине треугольной и равномерно распределенной нагрузок.
Исходные данные – по табл. 4.1.
 |
Рис. 4.1. Схема к задаче 4
Таблица 4.1. Исходные данные к задаче 4
| Вариант | b 1, м | b 2, м | z, м | p, кПа | Расчетная вертикаль |
| М1 | |||||
| M2 | |||||
| МЗ | |||||
| М1 | |||||
| М2 | |||||
| М3 | |||||
| М1 | |||||
| М2 | |||||
| М3 | |||||
| М1 | |||||
| М2 | |||||
| М3 | |||||
| М1 | |||||
| М2 | |||||
| М3 | |||||
| М1 | |||||
| М2 | |||||
| М3 | |||||
| М1 | |||||
| М2 | |||||
| М3 | |||||
| М1 | |||||
| М2 | |||||
| М3 | |||||
| М2 |
Пример
Построить эпюры вертикальных сжимающих напряжений в массиве грунта от действия полосовой нагрузки p =200 кПа, изменяющейся по закону прямой в точках на заданной вертикали и горизонтали, расположенной на расстоянии z =2 м от поверхности (рис. 4.2). Ширина треугольной нагрузки b 1 = 2 м, ширина прямоугольной нагрузки b 2 = 2 м. Точки по вертикали M3 на глубине 0, 1, 2, 4 и 6 м, по горизонтали на границах и в середине треугольной и прямоугольной нагрузок.
|
|
|
 |
Рис. 4.2. Схема расположения нагрузок и точек определения
вертикальных сжимающих напряжений
Решение
Примем координатную систему yz.
Для распределенной полосовой нагрузки шириной b, изменяющейся по закону треугольника, вертикальные напряжения в грунтовом массиве определяются по формуле
,
где Kz – коэффициент, зависящий от соотношений z / b и y / b и определяемый по [4], y – горизонтальная координата рассматриваемой точки от оси, проходящей через вершину треугольной нагрузки; z – вертикальная координата точки от ограничивающей плоскости.
Для равномерно распределенной полосовой нагрузки шириной b вертикальные напряжения в грунтовом массиве определяются по той же формуле, что и для треугольной, но горизонтальная координата y отсчитывается от оси симметрии прямоугольной нагрузки.
Вертикальные сжимающие напряжения от совместного действия треугольной и прямоугольной нагрузок определяются суммированием напряжений от соответствующих нагрузок.
Определим напряжения по вертикали М3.
Для точки, находящейся на глубине z 1=0, отношения 
; 
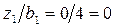для треугольной нагрузки; 
; 
для прямоугольной нагрузки. Значения коэффициентов Kz будут следующими: Kz 1 = 0; Kz 2 = 0,5.
Напряжение от совместного действия треугольной и прямоугольной нагрузок
Для точки, находящейся на глубине z 2=1 м, отношения ; 
; ; 
. Значения коэффициентов: Kz 1 = 0,003; Kz 2 = 0,5.
Напряжение
Для точки, находящейся на глубине z 3=2 м, отношения ; 
; ; 
. Значения коэффициентов: Kz 1 = 0,017; Kz 2 = 0,48.
Напряжение
Для точки, находящейся на глубине z 4=4 м, отношения ; 
; ; 
. Значения коэффициентов: Kz 1 = 0,045; Kz 2 = 0,41.
Напряжение
Для точки, находящейся на глубине z 5=6 м, отношения ; 
; ; 
. Значения коэффициентов: Kz 1 = 0,062; Kz 2 = 0,33.
Напряжение
Определим напряжения на горизонтальной прямой в точках A, В, С, D на глубине z =2 м.
Для точки А отношения 
; 
; 
; 
. Значения коэффициентов: Kz 1 = 0,127;
Kz 2 = 0,02.
|
|
|
Напряжение
Для точки B отношения 
; ; 
; . Значения коэффициентов: Kz 1 = 0,41;
Kz 2 = 0,08.
Напряжение
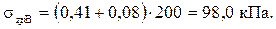
Для точки C отношения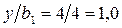 
; ; ; . Значения коэффициентов: Kz 1 = 0,353;
Kz 2 = 0,48.
Напряжение
Для точки D отношения 
; ; 
; . Значения коэффициентов: Kz 1 = 0,056;
Kz 2 = 0,82.
Напряжение
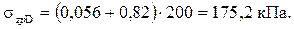
Для точки E напряжения
Построим эпюры вертикальных напряжений, откладывая ординаты соответствующих значений в расчетных точках по вертикали и горизонтали (рис 4.3).
Рис. 4.3. Эпюры вертикальных сжимающих напряжений
по горизонтальному и вертикальному сечениям
Задание 5. Определение устойчивости откоса методом
|
|
|
