 |
Корригирование эвольвентных цилиндрических прямозубых колес
|
|
|
|
Практические занятия по разделу ТММ
«ПРОЕКТИРОВАНИЕ ЗУБЧАТЫХ ЗАЦЕПЛЕНИЙ И МЕХАНИЗМОВ»
ПРОЕКТИРОВАНИЕ ТРЕХЗВЕННЫХ ЗУБЧАТЫХ ЗАЦЕПЛЕНИЙ
ОСНОВНАЯ ТЕОРЕМА ЗАЦЕПЛЕНИЯ
Общая нормаль к двум взаимоогибаемым кривым (профилям зубьев), проведенная в точке их касания, делит линию центров на части обратно пропорциональные угловым скоростям.
Пример № 1.1
Дано: два тела (рис. 1.1), насаженных на оси О1 и О2, контактирующих в точке К. Угловая скорость тела 1 равна ω1.
Определить: мгновенную угловую скорость ω2 тела 2.
Решение: проведем общую нормаль к профилям тел в точке их касания К до пересечения с линией центров О 1 О 2 в точке Р. В соответствии с основной теоремой зацепления
ω1 / ω2 = (О 2 Р)/(О 1 Р).
Откуда ω2 = ω1 (О 1 Р / (О 2 Р).
Пример № 1.2
Дано: два тела (рис. 1.2), насаженных на оси О1 и О2, контактирующих в точке К. Угловая скорость тела 1 равна ω1.
Определить: мгновенную угловую скорость ω2 тела 2.


ЛИНИЯ ЗАЦЕПЛЕНИЯ
Линией зацепления называется неподвижная прямая или кривая, в точках которой происходит касание зубьев.
Пример № 1.3
Дано: профиль зуба построен по эвольвенте 1, которую описывает произвольная точка прямой 2, перекатывающейся по основной окружности 3 с центром на оси колеса О (рис. 1.3).
Определить: линию зацепления.
Решение: выберем на профиле произвольную точку а и проведем из нее нормаль к профилю ─ прямую 4. По известному свойству эвольвенты, нормаль к ней является касательной к основной окружности 3. Отметим точку касания прямой 4 с окружностью 3 буквой d. Пересечение прямой 2 с окружностью 5 обозначим буквой с. Поскольку ba = cP как отрезки касательных между концентрическими окружностями, точка с принадлежит линии зацепления. Таким образом, прямая 2 является линией зацепления.
|
|
|

СОПРЯЖЕННЫЕ ПРОФИЛИ
Профили называются сопряженными, если их взаимодействие обеспечивает выполнение основной теоремы зацепления. Для круглых колес должно обеспечиваться постоянство передаточного отношения.
Пример № 1.4
Доказать сопряженность двух эвольвентных профилей зубьев.
Доказательство: В точке контакта сопряженных профилей должна существовать общая нормаль, которая в соответствии с основной теоремы зацепления проходит через полюс зацепления Р, делящий линию центров на части обратно пропорциональные угловым скоростям.
-Для каждого эвольвентного профиля нормаль является касательной прямой к основной окружности соответствующего колеса.
- Следовательно, точка контакта сопряженных эвольвентных профилей располагается на общей касательной к основным окружностям колес, и эвольвентное зацепление удовлетворяет основной теореме зацепления.
МИНИМАЛЬНОЕ ЧИСЛО ЗУБЬЕВ КОЛЕСА
ИЗГОТОВЛЕННОГО БЕЗ СМЕЩЕНИЯ
Если число зубьев на шестерне меньше предельного z мин., на шестерне произойдет подрез зуба при нарезании или интерференция зубьев в процессе зацепления.
Пример № 1.5
Определить zмин. на шестерне с внешним расположением зубьев при зацеплении его с внутренним колесом, у которого число зубьев z.
Решение: построение точки S ─ центра предельного колеса – показано на рис. 1.4.
Отсюда имеем: PS = Rмин = (АР)/ sin α;
АР = РК2 – АК2; РК2 = РО2 sin α;
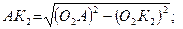
О2А =0,5 mz – ha*m; О2К2 = 0,5 mz cos α.
После преобразований получим
 (1.1)
(1.1)

Пример № 1.6
Определить зависимость zмин. для внутреннего зацепления от заданного передаточного числа u=z2 / z1 , ha*= 1 и α.
Решение: подставляя в формулу (1.1) z = z2 = z мин۰ u после преобразований получим:
 (1.2)
(1.2)
КОРРИГИРОВАНИЕ ЭВОЛЬВЕНТНЫХ ЦИЛИНДРИЧЕСКИХ ПРЯМОЗУБЫХ КОЛЕС
|
|
|
Колесо с числом зубьев z < zмин можно изготовить без подрезания, еслиприменить коррекцию, заключающуюся в том, что режущий инструмент отодвигается от оси заготовки. Необходимое смещение x m (мм) при заданном модуле m определяется по уравнению
x ≥ (zмин ─ z) / zмин. (1.3)
Если нарезаемое колесо внешнее, то при ha*= 1 и α = 200 принимаем
zмин = 17. Это значение соответствует нарезанию колеса рейкой.
Величина x называется коэффициентом смещения.
При нарезании колеса с Z< Zмин допустим отрицательный сдвиг, то есть приближение режущего инструмента к оси заготовки. Максимальный по абсолютной величине отрицательный сдвиг находим также по формуле (1.3).
Если нарезаемое колесо входит во внутреннее зацепление, то сдвиг также определяется по формуле (1.3), однако Zмин в этом случае вычисляем по зависимостям (1.1) или ( 1.2).
Пример № 1.7
Определить: основные размеры колеса с внешним расположением зубьев, если z= 10, m =12 мм, α = 200, ha*= 1.
Решение: величина коэффициента смещения
x ≥ (zмин ─ z) / zмин = (17─ 12)/17 = 0,412.
Абсолютный сдвиг рейки x m= 0,412۰ 12 = 4,94 мм.
Диаметры делительной окружности, окружности вершин зубьев и впадин равны: d = m z = 12۰ 10 = 120 мм;


Пример № 1.8
Определить абсолютный сдвиг при нарезании шестерни передачи с внутренним зацеплением, если z 1= 12, u= 4, m =12 мм, ha*= 1иα = 200.
Решение: z 2 = z1 u = 12۰4=48.
По формуле (1.1) получим

С учетом формулы (1.3) получим

|
|
|


