 |
Аналитическая теория эвольвентного зацепления
|
|
|
|
Уравнение эвольвенты имеет вид:
θ = tg α ─ α = inv α (инволюта α); соs α = rb / R,
где rb – радиус основной окружности; углы θ и α измеряются в радианах;
остальные обозначения указаны на рис. 1.5.

Толщина Sy зуба колеса с внешними зубьями по окружности произвольного радиуса ry:

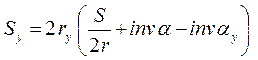 , (1.4)
, (1.4)
где S и r – соответственно толщина зуба и радиус делительной окружности.
r = mz/2;
 . (1.5)
. (1.5)
Радиус делительной окружности прямозубого зубчатого колеса
r = m z/ 2.
Для колес, нарезанных без смещения, межосевое расстояние
аw = (z1+ z2) m /2.
Радиусы окружностей вершин и впадин
ra = r + mn ha*; rf = r - mn (ha* + c*),
где ha* - коэффициент высоты головки зуба;
c*- коэффициент радиального зазора.
Пример № 1.9
Найти толщину зуба колеса с внешними зубьями для основной окружности Sa и для окружности вершин зубьев Sb при α =200, m = 10 мм, Z = 20, х = 0, ha*= 1.
Решение: радиус делительной окружности r = m z/ 2 = 100 мм.
Толщина зуба по делительной окружности S = π۰ m/ 2 = 15,7 мм.,
inv α = inv 200 = 0,0149; inv α b = 0.
По основной окружности: α b = 00; rb = r ۰cosα = 100۰0.94 = 94 мм.
 .
.
По окружности вершин зубьев: rа = r+ ha*m= 100+1۰10 = 110 мм.,
α a= arcos(rb/ rа) = arcos(94/ 110) = 31020’; inv α a = inv (31020’) = 0.0623.
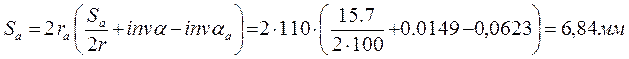 .
.
Пример № 1.10
По данным предыдущего примера установить: на каком радиусе толщина зуба равна нулю.
Решение: Принимая в формуле (1.4) Sy = 0, получим
 .
.
По таблице инволют αу = 35026’. cos αу = 0.815.
Следовательно ry = rb/ cos αу = 94 / 0.815 = 115 мм.
Пример № 1.11
Колесо с внешним зубом нарезано с положительным смещением х = 0,49. Остальные данные соответствуют примеру 1.9.
Найти толщину зуба колеса с внешними зубьями для основной окружности Sa и для окружности вершин зубьев Sb, для равносмещенного зацепления, когда х2= - х1.
|
|
|
Решение: толщина зуба по делительной окружности
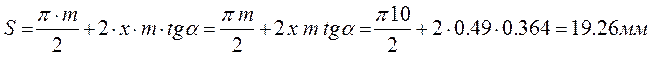 Радиус окружности вершин ra = r+m(x+ ha*)= 100+10 (0.49+1) = 114.9 мм.
Радиус окружности вершин ra = r+m(x+ ha*)= 100+10 (0.49+1) = 114.9 мм.
cos α a = rb/ ra = 94/114.9 = 0.817. α a= 35017’. Inv α a = 0.0912.
 .
.
 .
.
КОСОЗУБЫЕ ЦИЛИНДРИЧЕСКИЕ КОЛЕСА
На рис. 1.6.показана косозубая рейка (pn ─ нормальный шаг; pt ─ торцевой шаг; β – угол наклона зуба).

Зависимости между этими величинами такие:
pt = pn / cos β; mt = mn / cos β; tgα t = tgα n / cos β,
где mn, mt ─ нормальный и торцевой модули;
α n, α t ─ углы зацепления в нормальном и торцевом сечениях.
Как правило, нормальный модуль является стандартным.
Радиус делительной окружности косозубого зубчатого колеса
r = mt z/ 2 = z mn / (2 cos β).
Для косозубых колес, нарезанных без смещения, межосевое расстояние
аw = (z1+ z2) mn / (2 cos β).
Радиусы окружностей вершин и впадин
ra = r + mn ha*; rf = r - mn (ha* + c*),
где ha* - коэффициент высоты головки зуба;
c*- коэффициент радиального зазора.
Коэффициент перекрытия косозубых колес
εγ = εα + εβ = εα +(b sin β)/ pn,
где εα – коэффициент торцевого перекрытия, εβ – коэффициент осевого перекрытия, b – рабочая ширина венца колес.
Число зубьев эквивалентного колеса zv = z / cos3 β.
Подрез зубьев косозубого колеса будет, если
zv < zmin / cos3 β.
При ha* = 1, α n = 200 - zmin= 17.
Торцевой угол зацепления
 ,
,
где α t ─ угол зацепления исходного контура в нормальном сечении.
Межосевое расстояние
аw = (z1+ z2) mn cos α t / (2 cos α tw).
Пример № 1.12
Спроектировать косозубую передачу при условии устранения подреза зубьев при z1 = 8, z2 = 12, m = 6 мм, β = 300, ha* = 1, с*=0,25, α n = 200.
Решение: Число зубьев эквивалентных колес
zv1 = z1 / cos3 β = 8/ cos3 300 = 12,3;
zv2 = z2 / cos3 β = 12/ cos3 300 = 18,4.
Корригируем только шестерню: хn1 = (17 – 12.3) / 17 = 0.276; хn1 = 0.
Коэффициент смещения в торцевом сечении
хt1 = хn1 cos β = 0.276 ۰0.867 = 0.239.
Угол зацепления исходного профиля в торцевом сечении
tg α t = tg α n / cos β = tg 200 / cos 300 = 0,420; α t = 22047’; inv α t = 0,0224;
|
|
|
cos α t = 0,922.
Угол зацепления в торцевом сечении
 ;
;
α tv = 25035’; cos α tv = 0,902.
Межосевое расстояние
аw = (z1+ z2) mn cos α t / (2 cos α tw) =20۰6۰0,922/(2۰0,867۰0,902) = 70,77 мм.
Радиусы делительных окружностей, вершин и впадин зубьев такие:
r1 = z1 mn / (2 cos β) = 6۰8 / (2 ۰cos 300) = 27,75 мм;
r2 = z2 mn / (2 cos β) = 6۰12 / (2 ۰cos 300) = 41,58 мм;
rf1 = r1 - mn (ha* + c*- хn1) = 27,75 – 6 (1+ 0,25 - 0.276) = 21,85 мм;
rf2 = r2 - mn (ha* + c*- хn2) = 41,58 – 6 (1+0,25) = 34,08 мм;
rа1 = аw - rf2 - mn c* = 70,77 – 34,08 - 6۰0,25 = 35,19 мм;
rа1 = аw - rf1 - mn c* = 70,77 – 21,85 - 6۰0,25 = 47,72 мм.
ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ ПЛАНЕТАРНЫХ МЕХАНИЗМОВ РАЗЛИЧНЫХ СХЕМ
Планетарный однорядный механизм (механизм Джеймса).

Передаточное отношение можно определить:
1. графическим способом по чертежу;
2. аналитическим способом, используя формулу Виллиса.
Графический способ определения передаточного отношения.
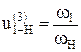
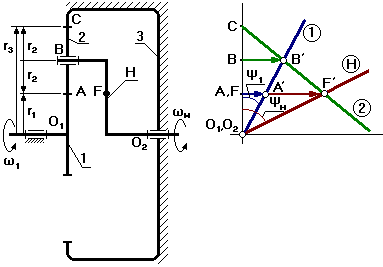
Выберем на водиле Н точку F которая расположена на том же расстоянии от оси О2, что и точка А.
Оси О1 и О2 расположены на одном уровне.
Для данной схемы входное звено – звено 1 (солнечное колесо), выходным является водило Н.
Зададимся отрезком АА’, который изображает линейную скорость колеса 1 в точке А. Т.к. колесо 1 вращается вокруг О1, то закон распределения линейной скорости по первому звену изображается прямой линией О1А’. Сателлит 2 в т.А имеет такую же линейную скорость, что и колесо 1. В т.С сателлит 2 имеет МЦС в абсолютном движении, т.к. идет контакт с неподвижным колесом 3. Закон распределения линейной скорости по второму колесу изображается прямой линией СА’. В т.В сателлит имеет линейную скорость, которая изображается отрезком ВВ’, однако т.В является также и осью водила Н, которое вращается вокруг О2. Следовательно, закон распределения линейной скорости по водилу изобразиться прямой линией О2В’. Для точки F водила линейная скорость изображается отрезком FF’.
От вертикали до линии распределения скоростей по водилу измеряем угол ψн, а от вертикали до линии распределения скоростей по колесу 1 измеряем угол ψ1. Так как углы ψ1 и ψн отложены от вертикали в одном направлении, то это показывает, что входное звено 1 и выходное звено вращаются в одном направлении.



Аналитический способ определения передаточного отношения.
|
|
|

Применим метод обращения движения, обратив планетарный механизм в непланетарный.

w1* = w1 – wН
w3* = w3 – wН = – wН


 – плюсовой механизм.
– плюсовой механизм.
Планетарный механизм со смешанным зацеплением
(с одним внешним и одним внутренним зацеплением).

Входное звено – первое звено;
 Выходное – водило.
Выходное – водило.
1– солнечное колесо;
2,3 – блок сателлитов;
4 – коронная шестерня;
Н – водило.
Выберем на выходном звене (на водиле) точку F так, чтобы O1A= O2F (оси O1 и O2 лежат на одной прямой - соосны).
1. Графический способ определения передаточного отношения


Отрезок АА' берем произвольно.
2. Аналитический способ определения передаточного отношения.
Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).
В обращенном движении каждое из звеньев будет иметь:
1 звено: ω*1 = ω1 + (–ωн)
2 звено: ω*2 = ω*3 = ω2 + (–ωн)
3 звено: ω*3 = ω*2 = ω3 + (–ωн)
4 звено: ω*4 = ω4 + (–ωн) = –ωн
5 звено: ω*н = ωн + (–ωн) = 0


если (1) переписать через количество зубьев, то

 плюсовой механизм.
плюсовой механизм.
2.3 Механизм с двумя внешними зацеплениями.
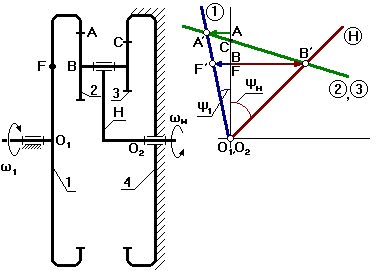 |
u(4)1–Н = 20 ÷ 50 при η = 0.99
Входное звено – водило;
Выходное – первое колесо.
u(4)1–Н = 1 / u(4)Н–1
Например, если u(4)Н–1= 20, то u(4)1–Н = 1 /20.
Графический способ.
Выберем точку F на входном звене так, чтобы O1F = O2B.
Точка С для данной схемы может располагаться как выше, так и ниже точки А. В зависимости от положения точки С план скоростей будет разный.
ψ1 и φ2 – направлены в разные стороны от вертикали. Следовательно, водило и колесо 1 вращаются в разные стороны.
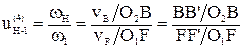

Аналитический способ.
Применим метод обращения движения.
u(4)1–Н = 1 – u(Н)1–4
Запишем передаточное отношение через число зубьев:

 Минусовой механизм
Минусовой механизм
2.4 Планетарный механизм с двумя внешними
Зацеплениями.

Механизм Давида
Применяется в приборных устройствах, так как u(4)Н–1 до 10 000.
|
|
|
Недостаток – низкий К.П.Д
Графический способ.
Выберем на водиле Н точку F так, чтобы O2F=O1A (валы O1 и O2 соосны). Точка С может быть выше или ниже точки А.
FF' – произвольный отрезок (линейная скорость точки F).
Для колес 2 и 3 точка С – МЦС.
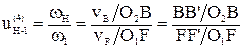

Аналитический способ.
u(4)1–Н = 1 – u(Н)1–4

 Минусовой механизм.
Минусовой механизм.

|
|
|


