Исходные данные задачи №8.01

Название	Непосредственно предшествующие операции	Длительность, недели
A	–
B	–
C	A,B
D	B
E	C
F	D
G	E,F

 

Решение

Построим сетевую модель и рассчитаем временные параметры событий (рис.8.3). При поиске критических путей на сетевом графике будем использовать следующие условия его критичности:

· необходимое условие – нулевые резервы событий, лежащих на критическом пути;

· достаточное условие – нулевые полные резервы работ, лежащих на критическом пути.

Согласно необходимому условию два полных пути сетевой модели (см. рис.8.3) и могут быть критическими. Проверим достаточное условие критичности для работ (1,2) и (1,3)

;

.

Путь , начинающийся с работы (1,3) не является критическим, т.к. как минимум одна из его работ (1,3,) не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ.

Таким образом, сетевая модель имеет единственный критический путь длительностью недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом.

Работа D или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа D задержится на 4 недели, то весь проект закончится на 1 неделю позже.

 

 

Рис.8.3. Сетевой график задачи №8.01

Задача №8.02

По данным о кодах и длительностях работ в днях (табл.8.2) постройте график привязки сетевой модели, определите критические пути и их длительность. Определите свободные и полные резервы каждой работы, отметьте на графике привязки свободные резервы работ.

Таблица 8.2

Исходные данные задачи №8.02

(i,j)	1,2	1,3	1,4	1,5	2,3	3,6	3,7	4,5	4,6	5,7	6,7
t(i,j), дни

 

 

Общие рекомендации

При поиске критических путей следует помнить, что признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы. Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта (). Кроме того, следует учесть, что критический путь является полным, т.е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.

Из вышеприведенных соображений следует способ определения критического пути на графике привязки (все найденные работы выписываются последовательно справа налево):

1) найти на графике привязки и выписать работу (i,j), которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие иметь номер завершающего события сети);

2) из всех работ сети (k,i), конечное событие которых i совпадает с начальным событием i работы (i,j), найденной в п.1), выбрать и выписать ту, которая на графике вплотную примыкает к работе (i,j);

3) из всех работ сети (l,k), конечное событие которых k совпадает с начальным событием k работы (k,i), найденной в п.2), выбрать и выписать ту, которая на графике вплотную примыкает к работе (k,i);

4) продолжать п.3) до тех пор, пока не будет найдена исходная работа сети, т.е. начинающаяся в нулевой момент времени (ее начальное событие будет иметь номер исходного события сети, например, 1).

Следует заметить, что если в сетевой модели несколько критических путей, то, выполняя вышеописанные действия, можно обнаружить несколько работ, удовлетворяющих сформулированным требованиям. В таком случае необходимо продолжать поиск по каждой из таких работ в отдельности. В сложных сетевых моделях подобные разветвления могут привести к большим затратам времени на поиск критически путей. Тем не менее, такой способ хорош для учебных целей, поскольку дает понимание значения критических работ в сетевой модели и учит "читать" и понимать график привязки.

Решение

I. Поиск критических путей

1) Построим график привязки (рис.8.4).

 

Рис.8.4. График привязки задачи №8.02

 

2) Начнем поиск критических путей (справа налево) с работ, завершающих проект. На графике привязки (см. рис.8.4) две работы (6,7) и (3,7), которые заканчиваются позже остальных в завершающем событии №7. Записываем работы, определенные как критические справа налево

;

(8.1)

.

3) Найдем критическую работу из , предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две – (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную "примыкает" на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (8.1)

.

(8.2)

4) Найдем критическую работу из , предшествующую (3,6). Код этой работы должен оканчиваться на 3. Таких работ две – (2,3) и (1,3). Но только одна из них, работа (2,3) по времени своего окончания вплотную "примыкает" на графике к началу работы (3,6). Допишем слева найденную критическую работу (2,3) к выражению (8.2)

.

(8.3)

5) Найдем критическую работу из , предшествующую (2,3). Код этой работы должен оканчиваться на 2. Работа (1,2) по времени своего окончания вплотную "примыкает" на графике к началу работы (2,3). С этой работы начинается критический путь

.

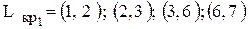6) Аналогичный поиск работ критического пути приводит к результату .

В другой форме записи и .

7) Для наглядности выделим на графике привязки критические работы жирной линией.

II. Поиск резервов работ

1) Для всех найденных критических работ впишем в табл.3 нулевые значения свободного и полного резервов. Рассмотрим некритические работы, начиная с конца табл.8.3.

Таблица 8.3

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: