Методические рекомендации по выполнению контрольной работы.

При решении задачи №1 необходимо, в первую очередь, определить единицу изучаемого множества, её первичные и вторичные признаки. По первичным признакам расчёт общей средней выполняется по схеме простой арифметической. Для вторичного признака определяем схему расчёта его индивидуальных значений и выражаем неизвестный признак через известные, используя их буквенные обозначения. Полученную расчётную схему применяем для определения общей средней.

Например, по условию задачи по нескольким предприятиям известна стоимость продукции - и выработка продукции на 1-го работника - . Так как признак является первичным, значение его общей средней рассчитаем по простой арифметической: .

Признак - вторичный, его индивидуальные значения получены по формуле:

Стоимость продукции: Численность работников. Численность работников по условию неизвестна, но её можно найти, если выразить через Стоимость продукции и Выработку на 1-го работника, то есть, Численность работников = . Тогда общая средняя будет рассчитана следующим образом: . Здесь использована средняя гармоническая взвешенная, а весом является первичный признак - Стоимость продукции. Следует помнить, что весом всегда выступает первичный признак, в какой бы сложной форме он ни присутствовал в используемом расчёте.

В задаче №2 предполагается выполнить расчёт абсолютных и относительных (нормированных) показателей различий 2-х структур. Средний арифметический показатель определяется по формуле: . Здесь и - показатели удельного веса, оценивающие отчётную и базисную структуры и выраженные в процентах: . Показатель определяет на сколько процентных пунктов в среднем отличается удельный вес каждой группы отчётной и базисной структуры. Относительная или нормированная оценка показывает сколько процентов составляют фактические различия двух структур от величины их предельных различий, составляющих 200%: процентов.

Коэффициент Гатева принадлежит к группе квадратических нормированных характеристик и показывает сколько процентов составляют фактические различия 2-х структур от их возможных различий: (процентов).

Аналогичную задачу относительной оценки различий двух структур решает коэффициент Рябцева. В отличие от коэффициента Гатева в нём иначе определяется возможное изменение структур: здесь это сумма квадратов сумм индивидуальных долей. Т.к. знаменатель коэффициента Рябцева больше, чем коэффициента Гатева, то К_{Рябцева} оценивает различия двух структур в меньшей мере по сравнению с оценками Гатева. Для более определённой характеристики выявленных различий используется шкала атрибутивных оценок: от тождественности структур до их полной противоположности.

Различия дух структур иллюстрируются столбиковой диаграммой, в которой рассматриваются фигуры, образовавшиеся в «зоне перехода» от одной структуры к другой.

Решение задачи №3 начинается с выяснения природы изучаемых явлений: относятся они к категории соизмеримых или несоизмеримых. Соизмеримые явления характеризуются одинаковой физической формой и одинаковыми потребительскими свойствами, назначением и использованием. Например, необходимо изучить зависимость и изменения значений признаков: W –стоимость произведённой продукции; T – численность работников; S – выработка продукции в среднем на 1-го работника. Зависимость признаков выражается соотношением: W_i = T_i * S_i.

Отсутствующие в условии задачи значения признаков у изучаемых единиц множества необходимо рассчитать: неизвестные значения W_i = T_i * S_i; неизвестные значения ; неизвестные значения .

Для анализа соизмеримых явлений используются система сводных индексов:

.

По условию задачи возможно рассмотреть ту часть системы, где более подробно анализируются факторы изменения среднего значения вторичного признака и рассчитать индекс переменного состава - , индекс постоянного состава - и индекс структурных сдвигов - , то есть систему сводных индексов в относительной форме:

.

Для расчёта указанных индексов необходимы значения общей средней выработки, которые определяются по формуле: .

Индекс переменного состава или индекс общей средней рассчитаем по схеме:

.

Пусть в нашем примере (тыс руб.); (тыс руб.), тогда или 107,0%. Общая средняя выработка отчётного периода оставила от уровня базисного периода 107%, то есть средняя выработка возросла на 7%

Индекс постоянного состава или индекс собственно выработки покажет как изменилась общая средняя под влиянием изменений индивидуальных значений вторичного признака; его значение определим по схеме:

.

В расчёте участвует условная средняя выработка, значение которой определяется на основе условной величины результата – условной стоимости продукции; её необходимо предварительно рассчитать.

В нашем примере

(тыс руб.). Тогда: или 104,3%.

Индекс постоянного состава показывает, что в результате изменения индивидуальной выработки работников общая средняя выработка в отчётном периоде составила 104,3%, то есть возросла на 4,3%.

Индекс структурных сдвигов оценивает изменения общей средней под влиянием изменений удельного веса единиц с высокими и низкими значениями вторичного признака-фактора.

или 102,6%.

В результате увеличения удельного веса работников с высоким уровнем выработки и уменьшения удельного веса работников с низким уровнем общая средняя выработка составила 102,6% от базисного уровня, то есть возросла на 2,6%. Если бы в структуре произошли противоположные изменения, тогда бы общая средняя уменьшилась, а величина индекса структуры была бы меньше единицы.

Представим полученные результаты в виде системы индексов в относительной форме:

; в нашем примере 1,070 = 1,043 * 1,026.

Увеличение общей средней выработки на 7% произошло в результате увеличения индивидуальной выработки на 4,3% и на 2,6% за счёт изменений в структуре работников. Из двух факторов, повлиявших на увеличение общей средней выработки, изменения индивидуальной выработки были более значительными, а их влияние на увеличение общей средней - более сильным, чем влияние изменений в структуре работников.

Решение задачи № 4 начинаем с определения вида динамического ряда: является он интервальным или моментным. Формальная отличительная черта моментного ряда – это заданность его значений на определённую дату. Уровни интервального динамического ряда формируются в течение определённого периода времени и поэтому приводятся за определённый отрезок, интервал времени.

Перечень показателей динамики за каждый год периода включает в себя:

а) абсолютный прирост – d (цепной и базисный);

б) темп роста (цепной и базисный) – К;

в) темп прироста (цепной и базисный) – T;

г) абсолютное значение 1% прироста – А.

Результаты оформляются в расчётной таблице.

 

С помощью показателей динамики за каждый год и графика проводится периодизация динамического ряда, то есть изучаемый отрезок времени разделяется на качественно однородные периоды, для каждого из которых характерна специфическая форма основной тенденции. Особенности каждого периода находят своё количественное отражение в значениях динамических средних. Перечень динамических средних включает: а) среднегодовой уровень ряда – ; б) среднегодовой абсолютный прирост – ; в) среднегодовой темп роста – . Порядок их расчёта рассмотрим на примере интервального и моментного динамических рядов.

Данные о производстве стальных труб в РФ за 1995 – 2005 гг., млн тонн

Годы
Bt	3,8	3,6	3,6	2,9	3,4	5,0	5,4	5,2	6,1	6,0	6,7
	I–й период	II-ой период

Здесь представлен интервальный ряд значений первичного признака, значения которого формируются за каждый год и каждый раз – заново, уровни ряда не содержат повторного счёта.

Анализ уровней ряда, показателей динамики за каждый год и графики выявляют два периода в производстве труб: 1995-1998 гг. – период сокращения производства; 1999-2005 г. – период увеличения размеров производства. Для количественной оценки особенностей каждого периода выполним расчёт системы динамических средних:

-среднегодовой уровень интервального ряда рассчитывается по простой средней арифметической - . Для первого периода расчёт средней выполняется из 4-х уровней ряда: млн тонн.

Для второго периода расчёт выполняется из 7 уровней:

млн тонн

Во втором периоде среднегодовой уровень был выше в 1,543 раза или на 54,3%.

Среднегодовой абсолютный прирост рассчитаем через уровни ряда:

для первого периода- 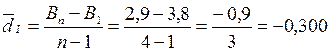млн тонн

для второго периода - 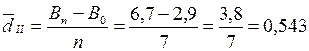млн тонн

В среднем за каждый год второго периода уровень ряды возрастал на 0,543 млн тонн, а за каждый год первого периода – он сокращался на 0,300 млн тонн. Среднегодовой абсолютный прирост во втором периоде был больше, чем в первом периоде в 1, 81 раза.

Среднегодовой темп роста также рассчитаем через уровни ряда:

для первого периода -

для второго периода

Уровень каждого следующего года во втором периоде был больше уровня предыдущего года в среднем в 1,127 раза, а в первом периоде – он составлял 0,914 раза. Во втором периоде ежегодный прирост в среднем равен 12,7%, а в первом периоде отмечается ежегодный спад в среднем на 8,6%. Различия в темпах прироста составляют 1,477 раза.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: