 |
Постулаты специальной теории относительности.
|
|
|
|
Лекция 7. Элементы теории относительности
План лекции
7.1. Принцип относительности Галилея.
7.2. Постулаты специальной теории относительности. Замедление времени.
7.3. Преобразования Лоренца для координат и времени.
7.4. Следствия из преобразований Лоренца.
7.5. Релятивистская динамика. Связь массы и энергии.
Принцип относительности Галилея
Рассмотрим инерциальные системы координат К (х,у, z) и К’ (х’,у’, z’). Пусть система К’ ’ движется относительно системы К с постоянной скоростью υ0. Для простоты будем считать параллельными оси координат К и К’ (x|| x’, y|| y’, z|| z’ - рис.7.1).
Рис.7.1
В момент времени t = 0 начало координат О’ совпадает с О.
В момент времени t точка М определяется радиус-вектором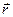 
относительно системы К и 
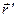относительно К’. Из рисунка 7.1 видно, что
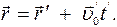(7.1)
При этом t = t’.
Запишем соотношение (7.1) в проекциях на оси координат:
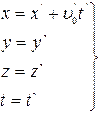(7.2)
Уравнения (7.1) и (7.2), выражающие координаты движущейся точки в неподвижной системе К через координаты подвижной системы К’ называются преобразованиями Галилея.
Продифференцируем (7.1) по времени t и получим уравнение
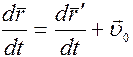
или
, (7.3)
которое представляет собой закон сложения скоростей в классической механике.
Так как
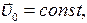
при дифференцировании (7.3) по времени t получим
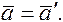(7.4)
Таким образом, ускорения в обеих системах отсчета одинаковы, т.е. ускорение инвариантно относительно преобразований Галилея.
|
|
|
Также
F = ma
инвариантно относительно преобразований Галилея, т.е.
F = F`.
Обобщая сказанное, можно сформулировать механический принцип относительности: уравнения механики Ньютона инвариантны относительно преобразований Галилея.
Постулаты специальной теории относительности.
Замедление времени
Специальная теория относительности (СТО) представляет собой современную теорию пространства и времени. СТО иначе называется релятивистской теорией. Механика тел,которые движутся со скоростями,близкими к скорости света c = 3·108 м/с называется релятивистской механикой. Классическая механика – механика малых скоростей (υ << c).
В СТО, как и в классической механике, предполагается, что время однородно (не зависит от выбора начала отсчета), пространство однородно (физические свойства системы и законы ее движения не зависят от выбора начала координат инерциальной системы) и изотропно (физические свойства и законы движения системы не зависят от выбора направления осей координат).
В основе СТО лежат два постулата, сформулированные Эйнштейном в 1905 г.
Первый постулат является обобщением механического принципа относительности Галилея на любые физические процессы. В любых инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинаково. Этот постулат называется принципом относительности или релятивистским принципом относительности Эйнштейна.
Второй постулат выражает принцип инвариантности скорости света: скорость света в вакууме не зависит от движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Из этого постулата следует, что события для наблюдателей, находящихся в неподвижной и подвижной системах отсчета, происходят не одновременно. Это можно показать.
|
|
|
Допустим один наблюдатель находится в неподвижной системе К (х, у, z), а другой в подвижной системе (в кабине) К’ (х’, у’, z’), которая движется (для простоты вдоль х) со скоростью υ (рис.7.1). Пусть t время, за которое световой импульс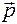 
проходит расстояние, равное высоте кабины. Для наблюдателя в неподвижной системе K, исходя из постоянства скорости света, световой импульс
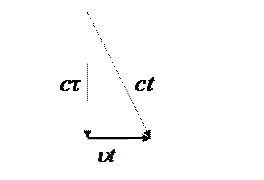
Рис.7.2
проходит путь, равный длине диагонали с t. Из треугольника (рис.7.2) получаем, что
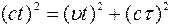(7.5)
откуда
и
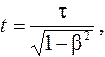(7.6)
где
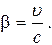
Из формулы (7.6) видно, что для неподвижного наблюдателя событие в движущейся системе длится дольше.
|
|
|
