 |
Преобразования Лоренца для координат и времени
|
|
|
|
Из постулатов СТО следует, что классические преобразования Галилея, описывающие переход от одной инерциальной системы отчета к другой, заменяются другими, получившими название преобразований Лоренца.
Преобразования Лоренца показывают, что при переходе от одной инерциальной системы отчета к другой изменяются не только пространственные координаты, но и время событий. Если учесть принцип симметрии, то при скорости υ движущейся системы отчета K’ (x’, y’, z’) относительно неподвижной К (х, у, z), скорость движения К относительно K’ будет - υ. Преобразования Галилея, с учетом преобразований Лоренца для координат и времени, при переходе от одной инерциальной системы отсчета к другой принимают вид:
К ® K’ K’ ® К
(7.7)
При малых скоростях υ << c преобразования Лоренца переходят в классические преобразования Галилея (в этом заключается принцип соответствия). При скоростях υ > c выражение (7.7) теряет физический смысл, так как координата и время становятся мнимыми. Это значит, что движение со скоростями больше скорости света в вакууме, невозможно.
7.4. Следствия из преобразований Лоренца
Первое следствие касается изменения размеров движущегося тела относительно неподвижного наблюдателя. Пусть система К’ движется со скоростью υ относительно К вдоль оси х (рис.7.3).
Длина стержня АВ, расположенного параллельно оси х, будет для системы К’:
ℓ 0 = х’ 2 – х’ 1,
а для системы К:
ℓ = х 2 - х 1.
Используя преобразования Лоренца (7.7), можно получить соотношение между ℓ и ℓ 0:
|
|
|
ℓ 0= х ’ 2 – х ’ 1=
т.е.
ℓ0=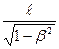 
, откуда 
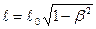. (7.8)
 |
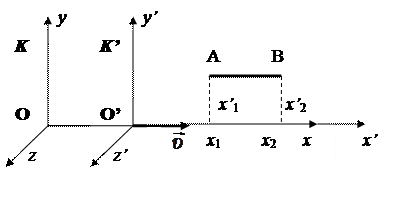Рис.7.3
Поскольку υ <c, то для наблюдателя в неподвижной системе отсчета К, длина движущегося стержня (с ним связана система К’) укорачивается. Данное явление называется лоренцевым сокращением длины.
Второе следствие касается разного течения времени в движущейся и неподвижной системе: для покоящегося наблюдателя событие длится дольше. Этот релятивистский эффект можно получить, используя преобразования Лоренца.
Пусть время начала и конца событий для наблюдателей в неподвижной и движущейся со скоростью υ системах отсчета будет соответственно (t 1 и t 2) и (t’ 1 и t’ 2). Тогда длительности событий для наблюдателей в этих системах:
t = t 2 - t 1 и t’ = t’ 2 – t’ 1. (7.9)
Учитывая выражения (7.7) и (7.9), получим
или
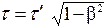(7.10)
Отсюда следует, что длительность событий минимальна в покоящейся системе отчета.
Релятивистский эффект замедления времени получил экспериментальное подтверждение. В состав космических лучей входят частицы, именуемые m-мезонами или мюонами. Они самопроизвольно распадаются на электрон (или позитрон) и два нейтрино. Скорость движения мюона близка к скорости света c, а время его жизни около 2·10-6с. За это время он может пройти путь порядка 600 м. Однако мюоны, преобразующиеся в космических лучах, на высоте 20-30 км достигают поверхности Земли. Это объясняется тем, что время жизни (2·10-6 с) измерено в движущейся системе отсчета, а для неподвижного наблюдателя, связанного с Землей время жизни мюона гораздо больше.
|
|
|
7.5. Релятивистская динамика. Связь массы и энергии
Все три закона динамики Ньютона выполняются и в рамках специальной теории относительности с учетом зависимости массы тела от скорости. Эта зависимость установлена экспериментально и выражается формулой
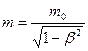, (7.11)
где m - масса покоящегося тела;
m 0 - релятивистская масса или масса движущегося тела.
Согласно СТО все законы природы и уравнения физических законов инвариантны при переходе от одной инерциальной системы отсчета к другой. Инвариантность выполняется и при преобразованиях Лоренца. Так в рамках СТО импульс тела описывается формулой
(7.12)
где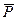 
- релятивистский импульс.
В релятивистской механике выполняются также законы сохранения релятивистского импульса и релятивистской массы.
Основной закон релятивистской динамики имеет вид:
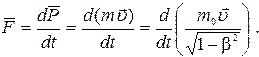(7.13)
Из теории относительности Эйнштейна вытекает фундаментальный закон природы: закон взаимосвязи массы и энергии. Этот закон формируется так: полная энергия системы E равна произведению полной релятивистской массы m на квадрат скорости света в вакууме с2. Математическое выражение этот закон имеет вид:
Е =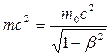 
, (7.14)
где m 0 - масса покоя, а β = υ/ c.
В релятивистской механике, также как и в механике классической, выполняется закон сохранения энергии: полная энергия системы остается неизменной.
В релятивистской механике изменение кинетической энергии Тк происходит при изменении релятивистской массы:
dTk = c 2 dm,
где dm - приращение релятивистской массы. Тогда
Tk =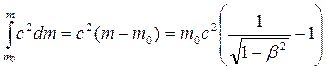 
. (7.15)
Полная энергия на основании закона взаимосвязи массы и энергии:
Е =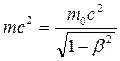 
Из (7.14) и (7.15) видно, что Tk = Е – Е 0.
Используя формулы (7.13) и (7.11) можно выразить полную энергию через импульс
Е 2 = Е 20 + (pc)2
или
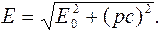
Закон взаимосвязи релятивистской массы и энергии подтвержден экспериментами и широко используется при ядерных реакциях и превращениях элементарных частиц.
|
|
|
Специальная теория относительности и квантовая механика служат теоретической базой современной физики.
К началу
К следующей лекции К содержанию
К титулу
|
|
|
