Соответствие переменных прямой и двойственной задачи

СБ	сj	A0							Q
Базисные переменные (БП)	х1	х2	х3	х4	х5	х6
	x4								65/4
	x5								28/3
	x6								13/11
zj-cj		-32	-67	-43
	х4	663/11	7/11		96/11			-4/11	663/7
	х5	538/11	38/11		34/11			-6/11	269/19
	х2	13/11	1/11		9/11			1/11
zj-cj	871/11	-285/11		130/11			67/11
	х4			-7				-1
	х5			-38	-28			-4
	х1
zj-cj

 

Задача решается на максимум.

Т.к.все оценки индексной строки в последней симплексной таблице неотрицательны, то найденный опорный план оптимален.

(13; 0; 0; 52; 4; 0) f()= 32*13+ 67*0+43*0=416

Основные переменные x₁=13, x₂=0, x₃=0 означают, что продукции П₁ надо выпустить 13 ед., а продукции П₂ и П₃ выпускать не следует.

Т.к. x₄=52, x₅=4, то первый и второй ресурсы избыточны, их остается в избытке в количествах 52 ед.и 4 ед.соответственно. Т.к. x₆=0, то третий ресурс используется полностью.

Полученный оптимальный план является единственным.

Во взаимодвойственных задачах линейного программирования первоначальным переменным ПЗЛП соответствуют дополнительные переменные ДЗЛП и аналогично первоначальным переменным ДЗЛП соответствуют дополнительные переменные ПЗЛП.

Установим соответствие переменных прямой и двойственной задачи для варианта 4:

х1 y4

х2 y5

х3 y6

х4 y1

х5 y2

х6 у3

 

Имеем: (0; 0; 32; 0; 285; 245)

q()=65*0+56*0+13*32=416= f()

Двойственные переменные показывают меру дефицитности ресурсов, они численно равны изменению целевой функции при изменении соответствующего ресурса на единицу. Первый и второй ресурс избыточны и их увеличение не приводит к изменению целевой функции. Увеличение количества третьего ресурса на единицу приводит к увеличению значения целевой функции на y₃=32 ед.

Дополнительные двойственные переменные показывают меру убыточности продукции, которую согласно оптимальному плану выпускать не следует. Значит y₅=285 говорит о том, что стоимость ресурсов, расходуемых на единицу производства продукции второго вида (в оптимальных оценках), превосходит стоимость единицы этой продукции на y₅=285 ед.

В самом деле:

a₁₂*y₁+a₂₂*y₂+a₃₂*y₃=4*0+6*0+11*32=352

352-c₃=352-67=285= y₅

Аналогично, y₆ говорит о том, что стоимость ресурсов, расходуемых на единицу производства продукции третьего вида (в оптимальных оценках), превосходит стоимость единицы этой продукции на y₆=245 ед.

В самом деле:

a₁₃*y₁+a₂₃*y₂+a₃₃*y₃=12*0+8*0+9*32=288

288-c₃=288-43=245= y₆

Раскроем состав двойственных переменных.

y₁=0*1+0*0+32*0=0;

y₂=0*0+0*1+32*0=0;

y₃=0*(-1)+0*(-4)+32*1=32

Экономически, например, для y₃=32 это означает, что увеличение третьего ресурса на единицу повлечет за собой увеличение выпуска продукции П₁ на 1 ед., сокращение избыточного первого ресурса на 1 ед., а также сокращение избыточного первого ресурса на 1 ед., а также сокращение избыточного второго ресурса на 4 ед.

4. Расчет границ изменения дефицитных ресурсов, в пределах которых не изменится структура оптимального плана

Ресурсы, которые используются полностью, называются дефицитными. Признаком дефицитности ресурсов является отличие от нуля соответствующей данному ресурсу двойственной переменной и равенство нулю соответствующей дополнительной переменной.

В рассматриваемом случае все три ресурса используются полностью, следовательно, являются дефицитными.

Для исследования границ изменения первого вида ресурса Р₁ из последней симплекс-таблицы составляют систему неравенств для базисных переменных ПЗЛП, используя элементы из столбца свободных членов b_i и столбца, соответствующего переменной у₁. Коэффициенты из столбца «у₁» умножают на искомое изменение D b₁ запаса ресурса Р₁:

Þ .

Анализ дефицитного ресурса Р₃ имеем: b₃=13. Заменим b₃=13 на b’₃= b₃ +∆ b₃

Тогда последняя симплексная таблица примет вид:

БП	СБ	Ао	…..x6……
…..0……
x4		52-∆ b3	-1
x5		4-4∆ b3	-4
x1		13+∆ b3
zj-cj	416+32∆ b3

 

Значит, т.к. оптимальный план-опорный, то x_i≥0 и следовательно:

Þ Þ

-13≤∆ b₃≤1

b₃-13≤ b₃’≤ 1+ b₃

13-13≤ b₃’≤1+13

0≤ b₃’≤14

5. Уточнение значения недефицитных ресурсов, при которых оптимальный план не изменится

Анализ недефицитных ресурсов b₁ и b₂

Заменим b₁ на b₁’=b₁ + ∆ b₁

Тогда получим:

52+∆ b₁≥0

∆ b₁≥-52

60-52≤b₁+∆ b₁≤+∞

8≤ b’₁<+∞

 

Заменим b₂ на b₂’=b₂ + ∆ b₂

Тогда получим:

4+∆ b₂≥0

∆ b₂≥-4

56-4≤b₂+∆ b₂≤+∞

52≤ b’₂<+∞

6. Расчет границ изменения цены изделия, попавших в оптимальный план производства, в пределах которых оптимальный план не изменится

Анализ коэффициентов целевой функции (цен изделий) при базисных переменных имеем: C₁=32.

Заменим С₁=32 на С₁’= С₁+∆С₁=32+∆С₁

В последней симплексной таблице получим:

СБ	сj	A0	32+∆С1
Базисные переменные (БП)	х1	х2	х3	х4	х5	х6
	x4			-7				-1
	x5			-38	-28			-4
32+∆С1	x1
D j	416+13∆С1		285+11∆С1	245+9∆С1			32+∆С1

 

Þ Þ

-285/11≤∆ C₁≤+∞

32-285/11≤ ∆ C’₁≤32+∞

67/11≤ ∆ C’₁≤+∞

7. Определение величины ∆ b_s ресурса Р_s, введением которого в производство можно компенсировать убыток и сохранить максимальный доход на прежнем уровне (ресурсы предполагаются взаимно заменяемыми), получаемый при исключении из производства ∆ b_r единиц ресурса Р_r

Величину ∆b₁ ресурса Р₁, которым можно компенсировать убыток и сохранить максимальный доход на прежнем уровне, при исключении ∆b₃=0,1 ед.ресурса Р₃, определим, используя коэффициенты взаимозаменяемости ресурсов.

Матрица взаимозаменяемости ресурсов имеет вид:

К i	1 (y1=0)	2 (y2=0)	3 (y3=32)
1 (y1=0)		-	∞
2 (y2=0)	-		∞
3 (y3=32)

 

Т.к. ƞ₁₃=∞, то ∆b₁=∆b₃ ƞ₁₃=0,1*∞=∞

Это означает, что компенсировать исключение из производства ∆b₃= 0,1 ед.ресурса Р₃ никаким количеством ресурса Р₁ невозможно компенсировать, поскольку ресурс Р₁ избыточный, а ресурс Р₃ дефицитный.

 

8. Оценка целесообразности приобретения ∆ b_k единиц ресурса Р_k по цене с_k за единицу

Для оценки целесообразности приобретения дополнительного количества ресурса ∆ b_i вида i по цене с_k необходимо сравнить предлагаемую цену с рассчитанной ранее теневой ценой этого ресурса . Приобретение дополнительного количества ресурса целесообразно, если выполняется условие непревышения новой цены над теневой ценой

с_k £ .

В противном случае приобретение дополнительного количества ресурса нецелесообразно.

Оценим целесообразность приобретения ∆b₂=0,5 ед.ресурса Р₂ по цене С=24 ед.

Затраты на приобретение S=∆b₂*C=0,5*24=12 (ед.)

Изменение целевой функции при введении в производство ∆b₂=0,5 ед. ресурса Р составит ∆F=∆b₂*y₂=0,5*0=0 (∆F₂=0, т.к.ресурс Р₂ избыточный).

Т.к. ∆F-S=0-12=-12<0, то приобретение ∆b₁=0,5 ед.ресурса Р₂ по цене С=24 ед. нецелесообразно.

9. Оценка целесообразности выпуска нового изделия П₄, на единицу которого ресурсы Р₁, Р₂, Р₃ расходуются в количествах a₁₄, a₂₄, a₃₄ единиц, а цена единицы изделия составляет с₄ денежных единиц

Включение дополнительного вида продукции n+1 в план производства целесообразно, если соотношение дополнительных затрат и цены реализации дополнительного вида продукции удовлетворяет следующему условию

.

Оценим целесообразность выпуска продукции П₄ с характеристиками.

a₁₄=4, a₂₄=15, a₃₄=2, c₄=70

Затраты на производство единицы продукции П₄:

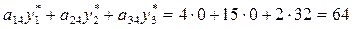ден. ед.

Т.к. с₄ = 70>64, то продукцию П₄ выпускать целесообразно.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: