Решение прямой и двойственной задач линейного программирования в среде Microsoft Exсel

Рис.1- ввод исходных данных.

Рис.2-настройка опции “Поиск решения”

Рис.3,4 – вывод результатов.

Рис.5,6,7 – отчеты по результатам, устойчивости, пределам.

 

 

 

 

Б. Двойственный симплекс-метод

1. Выражение базисных переменных ПЗЛП и ДЗЛП через свободные.

Канонический вид ПЗЛП:

Канонический вид ДЗЛП:

Выразим базисные переменные ПЗЛП и ДЗЛП через свободные:

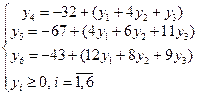
2.Определение исходного решения прямой и двойственной задач и проверка его на оптимальность.

Симплексная таблица двойственного симплекс-метода для варианта 4 имеет следующий вид:

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4
y2	x5
y3	x6
cj		-32	-67	-43

 

Решение ПЗЛП выписывается по строкам, значения базисных переменных берутся из столбца b_i, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: = (0, 0, 0, 65, 56, 13), = 0.

Решение ДЗЛП выписывается по столбцам, значения базисных переменных берутся из строки c_j, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: = (0, 0, 0, -32, -67, -43), = 0.

Данное решение не является оптимальным, поскольку решение не допустимое (не выполнено условие неотрицательности переменных), ему соответствуют отрицательные элементы в строке . Поэтому следует провести замену переменных в базисе.

3. Выбор разрешающей строки.

Правила выбора разрешающей строки

Находят отрицательный элемент в строке . В столбце над этим найденным элементом выбирают любой положительный элемент, эта строка – разрешающая.

Если в столбце над найденным элементом нет положительных элементов, то ПЗЛП не имеет смысла (целевая функция не ограничена в области допустимых решений), а ДЗЛП не имеет решения.

В строке f(x) три отрицательных элемента. Выбираем например «-32», а над ним выбираем элемент из второй строки «4». Следовательно, вторая строка – разрешающая.

Элементы строки делим на соответствующие элементы разрешающей строки и из полученных отношений выбираем максимальное отношение: .

Значит третий столбец разрешающий.

Разрешающим элементом является «8», стоящий на пересечении второй строки и третьего столбца. Заполняем нижние части клеток таблицы.

 

 

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	-40	-40	-12	-152
y2	x5			«8»
y3	x6	-28		-9	-400
cj		- 32 -84	- 67 -278	- 43

Строим новую симплекс-таблицу:

	yбаз	y4	y5	y1
yсв	xсв xбаз	- x1	- x2	- x5	bi
y1	x4	-5	-5	-3/2	-19
y6	x3	1/2	3/4	1/8
y3	x6	-7/2	17/4	-9/8	-50
cj		-21/2	-139/4	43/8

 

В строке f(x) выбираем элемент «-139/4», а над ним выбираем элемент из третьей строки 17/4. Находим:

Значит разрешающий элемент “17/4”, стоящий на пересечении третьей строки и второго столбца.

Заполняем нижние части клеток таблицы.

	yбаз	y4	y5	y2
yсв	xсв xбаз	- x1	- x2	- x5	bi
y1	x4	-5 -155/4	-5	-3/2 -12	-19 -1323/4
y6	x3	1/2 19/4	3/4 -3/4	1/8 11/8	269/4
y3	x6	-7/2 -7/2	«17/4»	-9/8 -9/8	-50 -50
cj		- 21/2 -665/4	- 139/4 139/4	43/8 -65/4	-1833/4

Строим новую симплекс-таблицу:

	yбаз	y4	y3	y2
yсв	xсв xбаз	- x1	- x6	- x5	bi
y1	x4	-155/17	20/17	-48/17	-1323/17
y6	x3	19/17	-3/17	11/34	269/17
y5	x2	-14/17	4/17	-9/34	-200/17
cj		-665/17	139/17	-65/17	-1833/17

 

В строке f(x) выбираем элемент «-65/17», а над ним выбираем элемент 11/34. Тогда:

Разрешающий элемент 11/34

Заполняем нижние части клеток таблицы.

 

	yбаз	y4	y3	y2
yсв	xсв xбаз	- x1	- x6	- x5	bi
y1	x4	-155/17 7/34	20/17 -2/17	-48/17 48/17	-1323/17 39/2
y6	x3	19/17 19/17	-3/17 -3/17	«11/34»	269/17 269/17
y5	x2	-14/17 1/34	4/17 1/34	-9/34 9/34	-200/17 13/34
cj		- 665/17 -285/34	139/17 67/34	-65/17 65/17	-1833/17 871/34

Строим новую симплекс-таблицу:

	yбаз	y4	y3	y6
yсв	xсв xбаз	- x1	- x6	- x3	bi
y1	x4	7/11	-4/11	96/11	663/11
y2	x5	38/11	-6/11	34/11	538/11
y5	x2	1/11	1/11	9/11	13/11
cj		-285/11	67/11	130/11	871/11

 

В строке f(x) выбираем элемент «-285/11», а над ним выбираем элемент 1/11, который является разрешающим элементом.

Заполняем нижние части клеток таблицы.

 

	yбаз	y4	y3	y6
yсв	xсв xбаз	- x1	- x6	- x3	bi
y1	x4	7/11 -7/11	-4/11 -1/11	96/11 3/11	663/11 52/11
y2	x5	38/11 -38/11	-6/11 -4/11	34/11 -28/11	538/11 4/11
y5	x2	«1/11»	1/11 1/11	9/11 9/11	13/11 13/11
cj		- 285/11 285/11	67/11 32/11	130/11 245/11	871/11 416/11

Строим новую симплекс-таблицу:

	yбаз	y5	y3	y6
yсв	xсв xбаз	- x2	- x6	- x3	bi
y1	x4	-7	-1
y2	x5	-38	-4	-28
y4	x1
cj

 

Оптимальное решение ПЗЛП: = (13, 0, 0, 52, 4, 0), =416,

оптимальное решение ДЗЛП: 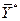= (0, 0, 32, 0, 285, 245), 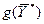=416.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: