 |
Расчет пусковых характеристик.
|
|
|
|
а) Расчёт токов с учётом изменения параметров под влиянием эффекта вытеснения тока (без учёта влияния насыщения от полей рассеяния).
105. Активное сопротивление обмотки ротора с учётом влияния эффекта вытеснения тока [ 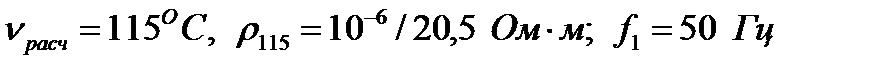 ]. По рисунку 8.76 [1, стр.411]:
]. По рисунку 8.76 [1, стр.411]:
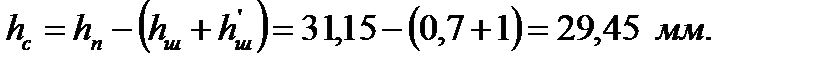
106. Приведём расчёт для 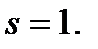 При литой алюминиевой обмотке и расчётной температуре
При литой алюминиевой обмотке и расчётной температуре 
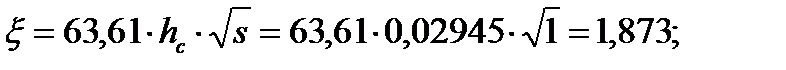
По рисунку 8.57 [1, стр.366] при 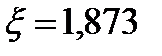 находим
находим 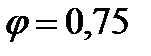 .
.
107. Глубина проникновения тока:
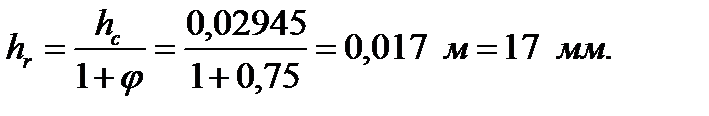
108. Коэффициент 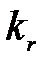 для круглых стержней находим по отношению площадей всего сечения стержня и сечения, ограниченного высотой
для круглых стержней находим по отношению площадей всего сечения стержня и сечения, ограниченного высотой 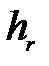 , то есть:
, то есть:
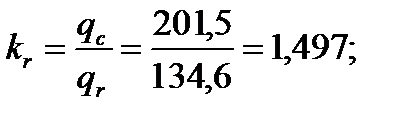
где  площадь сечения, ограниченного высотой
площадь сечения, ограниченного высотой 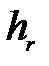 :
:
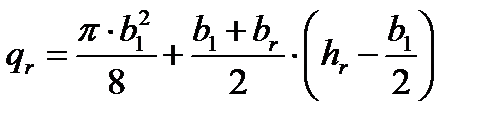 ,
,
где
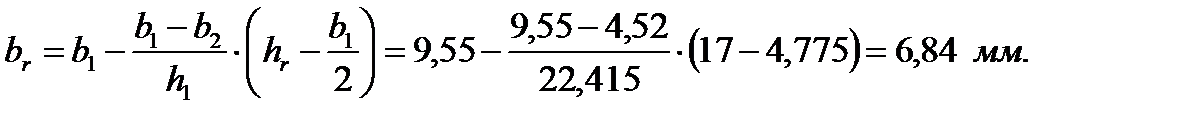
Соответственно:
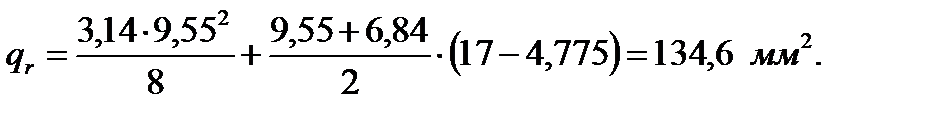
109. Коэффициент общего увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока:

где 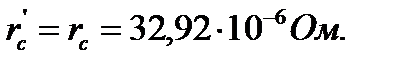
110. Приведенное сопротивление ротора с учётом влияния эффекта вытеснения тока:
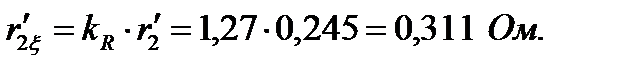
Индуктивное сопротивление обмотки ротора с учётом влияния эффекта вытеснения тока по рис.8.58 [3, стр. 366] при 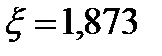 ,
, 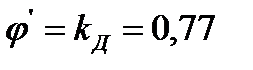
111. Коэффициент магнитной проводимости пазового рассеяния с учётом эффекта вытеснения тока:
 ,
,
Где
 ,
,
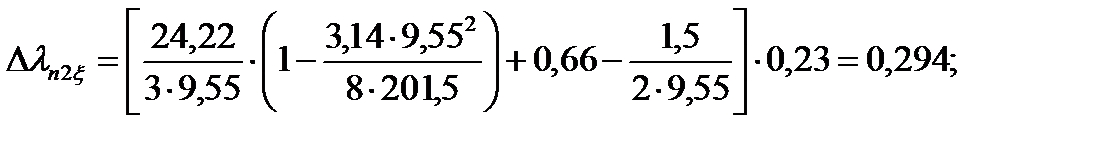 ,
,
где 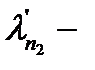 коэффициент магнитной проводимости участка паза, занятого проводником с обмоткой.
коэффициент магнитной проводимости участка паза, занятого проводником с обмоткой.
Следовательно:
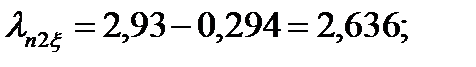
112. Определим изменение индуктивного сопротивления фазы обмотки ротора от действия эффекта вытеснения тока:
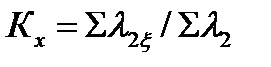
то есть:
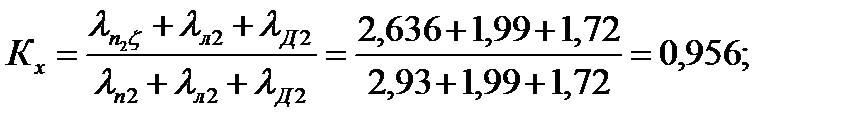
Соответственно:
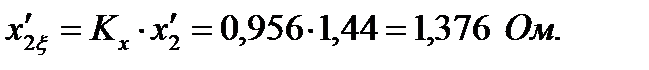
113. Учитывая, что индуктивное сопротивление взаимной индукции  с уменьшением насыщения магнитопровода увеличивается, в расчете пусковых характеристик для скольжений
с уменьшением насыщения магнитопровода увеличивается, в расчете пусковых характеристик для скольжений 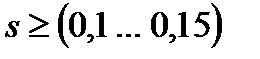 , оно может быть принято равным:
, оно может быть принято равным:
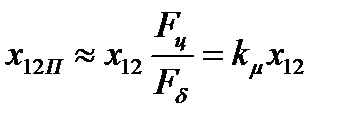 ,
,
то есть:
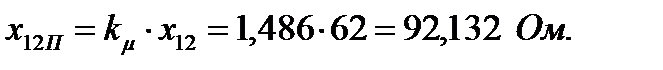
Не внося большой погрешности, в расчетных формулах пусковых режимов пренебрегают сопротивлением  . Это оправдано при токах, заметно превышающих номинальный, так как электрические потери в обмотках, возрастающие пропорционально квадрату тока, многократно превышают потери в стали, для учета которых в схему замещения введен параметр
. Это оправдано при токах, заметно превышающих номинальный, так как электрические потери в обмотках, возрастающие пропорционально квадрату тока, многократно превышают потери в стали, для учета которых в схему замещения введен параметр  .
.
|
|
|
114. При этом допущениях коэффициент:
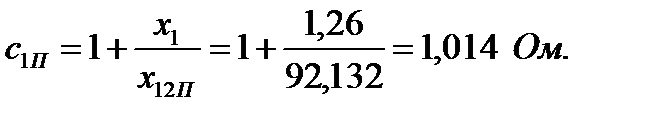
115. Расчёт токов с учётом влияния эффекта вытеснения тока для 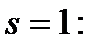
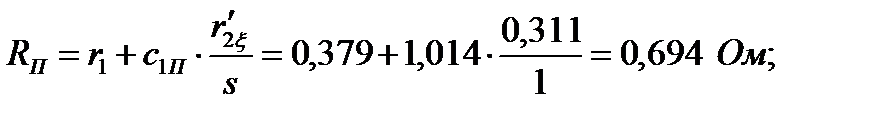

Следовательно:
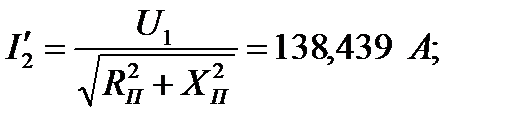
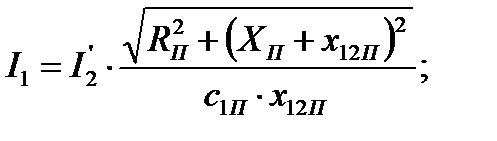
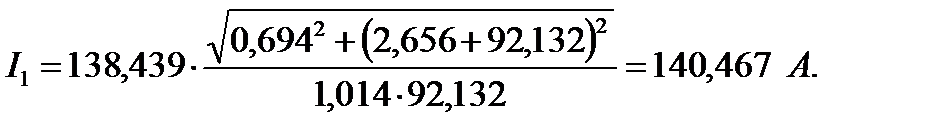
116. Аналогично проводим расчёты и для 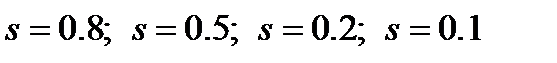 и для критического скольжения, вычисляемого по формуле:
и для критического скольжения, вычисляемого по формуле:
 .
.
Получим
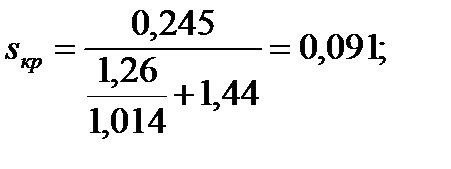
Данные расчётов пусковых характеристик сведены в таблицу 8:
Таблица 8
| № п/п | Расчётные формулы | Размерность | Скольжение s | |||||
| 0,8 | 0,5 | 0,2 | 0,1 | 
| ||||
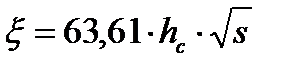
| – | 1,873 | 1,676 | 1,325 | 0,838 | 0,592 | 0,565 | |

| – | 0,75 | 0,48 | 0,21 | 0,044 | 0,011 | 0,009 | |
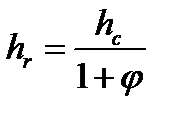
| мм | |||||||

| – | 1,497 | 1,3 | 1,121 | 1,018 | 0,998 | 0,997 | |
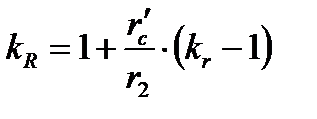
| – | 1,27 | 1,165 | 1,066 | 1,01 | 0,999 | 0,998 | |
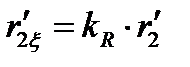
| Ом | 0,311 | 0,285 | 0,261 | 0,247 | 0,245 | 0,245 | |

| – | 0,77 | 0,85 | 0,92 | 0,97 | 0,98 | 0,98 | |

| – | 2,636 | 2,74 | 2,83 | 2,89 | 2,9 | 2,9 | |
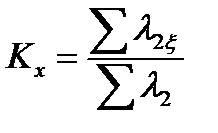
| – | 0,956 | 0,971 | 0,985 | 0,994 | 0,996 | 0,996 | |

| Ом | 1,376 | 1,398 | 1,42 | 1,432 | 1,434 | 1,434 | |
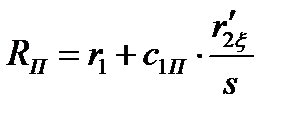
| Ом | 0,694 | 0,741 | 0,909 | 1,633 | 2,86 | 3,1 | |

| Ом | 2,656 | 2,678 | 2,698 | 2,712 | 2,715 | 2,715 | |

| А | 138,44 | 136,76 | 133,5 | 96,35 | 92,142 | ||

| А | 140,47 | 138,8 | 135,5 | 121,89 | 97,87 | 93,6 |
б) Расчёт пусковых характеристик с учётом влияния вытеснения тока и насыщения от полей рассеяния.
117. Расчёт проводим для точек характеристик, соответствующих 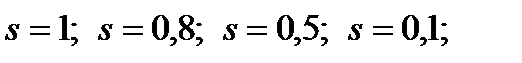
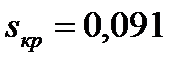 , при этом используем значения токов и сопротивлений для тех же скольжений с учётом влияния вытеснения тока (таблица 7).
, при этом используем значения токов и сопротивлений для тех же скольжений с учётом влияния вытеснения тока (таблица 7).
Данные расчётов сведены в таблицу 8. Подробный расчёт приведём для 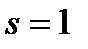 .
.
Принимаем 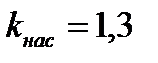 , тогда средняя МДС обмотки, отнесённая к одному пазу обмотки статора:
, тогда средняя МДС обмотки, отнесённая к одному пазу обмотки статора:
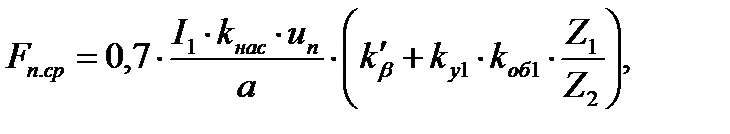
где 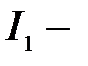 ток статора, соответствующий расчётному режиму без учёта насыщения;
ток статора, соответствующий расчётному режиму без учёта насыщения; 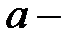 число параллельных ветвей обмотки статора;
число параллельных ветвей обмотки статора;  число эффективных проводников в пазу статора;
число эффективных проводников в пазу статора;  коэффициент, учитывающий уменьшение МДС паза, вызванное укорочением шага обмотки;
коэффициент, учитывающий уменьшение МДС паза, вызванное укорочением шага обмотки; 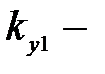 коэффициент укорочения шага обмотки.
коэффициент укорочения шага обмотки.
|
|
|

118. По средней МДС 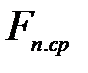 рассчитываем фиктивную индукцию потока рассеяния в воздушном зазоре:
рассчитываем фиктивную индукцию потока рассеяния в воздушном зазоре:
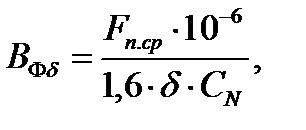
где коэффициент
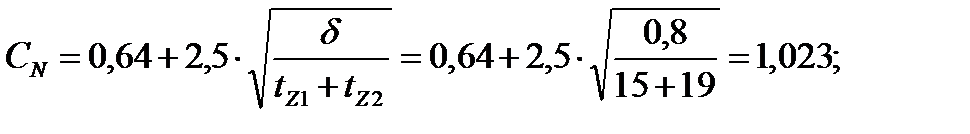
Следовательно:
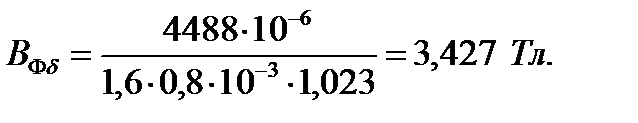
По полученному значению 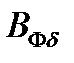 определяют отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом
определяют отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом 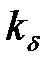 , значение которого находим по кривой
, значение которого находим по кривой 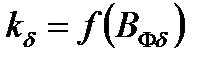 рисунка 8.61 [3, стр. 370]: при
рисунка 8.61 [3, стр. 370]: при 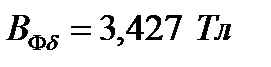 ,
, 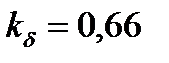 .
.
119. Значение дополнительного эквивалентного раскрытия пазов статора:

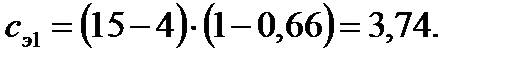
120. Коэффициент магнитной проводимости пазового рассеяния при насыщении 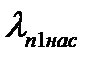 определяют для статора из выражения:
определяют для статора из выражения:
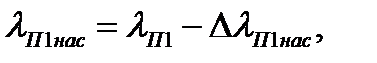
где 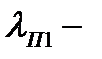 проводимость, рассчитанная без учёта насыщения,
проводимость, рассчитанная без учёта насыщения,  вызванное насыщением от полей рассеяния уменьшение коэффициента магнитной проводимости рассеяния закрытого паза:
вызванное насыщением от полей рассеяния уменьшение коэффициента магнитной проводимости рассеяния закрытого паза:
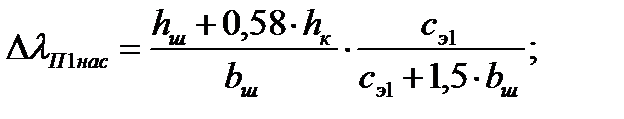
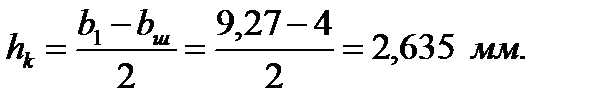
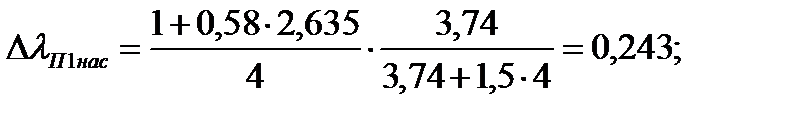
Следовательно:
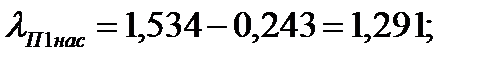
121. Коэффициент проводимости дифференциального рассеяния при насыщении участков зубцов статора:
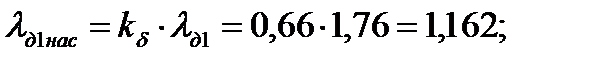
122. Индуктивное сопротивление обмотки статора с учётом насыщения от полей рассеяния определяем по отношению сумм коэффициентов проводимости, рассчитанных без учёта и с учётом насыщения от полей рассеяния:


123. Для короткозамкнутых роторов дополнительное раскрытие рассчитываем по формуле:
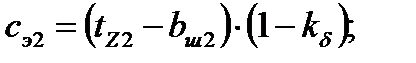
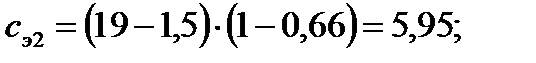
124. Коэффициент магнитной проводимости пазового рассеяния при насыщении 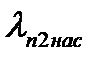 определяют для ротора из выражения:
определяют для ротора из выражения:

где

Соответственно:
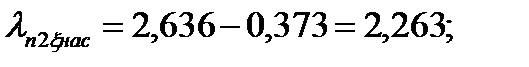
125. Коэффициент проводимости дифференциального рассеяния при насыщении участков зубцов ротора:

126. Для ротора принимаем отношение сумм проводимостей, рассчитанных без учёта влияния насыщения и действия вытеснения тока (для номинального режима) и с учётом этих факторов:
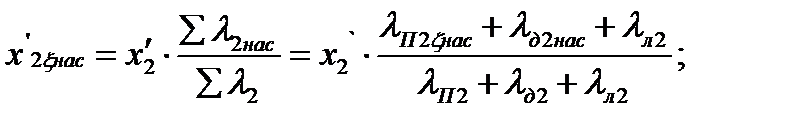

127. Коэффициент:

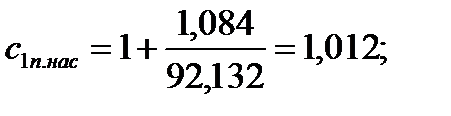
128. Расчёт токов и моментов:
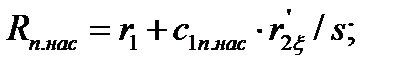

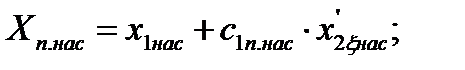
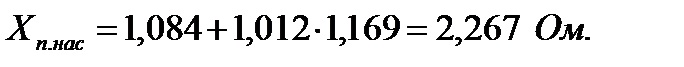
129. Ток в обмотке ротора:

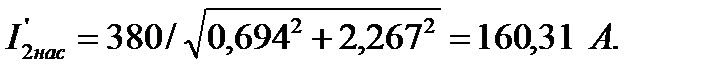
Соответственно:
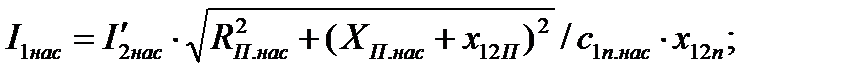
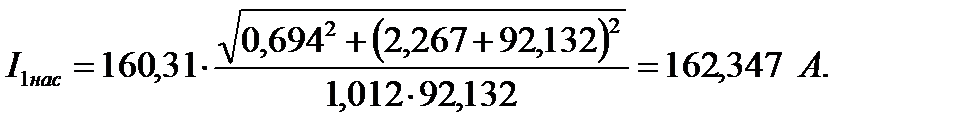
130. Кратность пускового тока с учётом влияния вытеснения тока и насыщения:
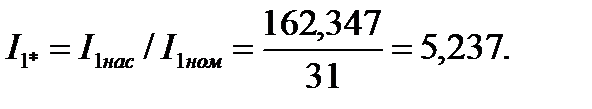
131. Кратность пускового момента с учётом влияния вытеснения тока и насыщения:
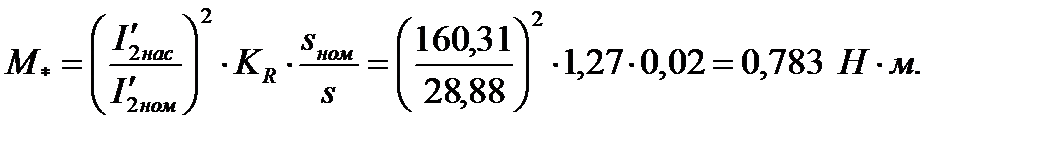
132. Полученный в расчёте коэффициент насыщения:
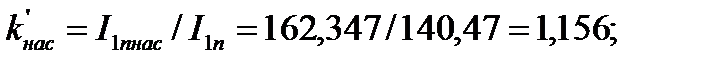
Таблица 9
| № п/п | Расчётные формулы | Размерность | Скольжение s | |||||
| 0.8 | 0.5 | 0.2 | 0.1 | 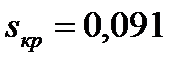
| ||||

| ----- | 1,3 | 1,25 | 1,2 | 1,15 | 1,1 | 1.3 | |
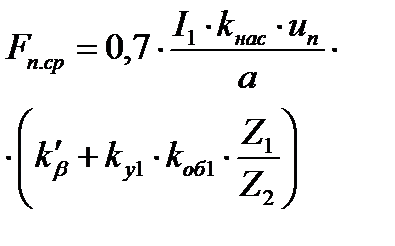
| А | |||||||
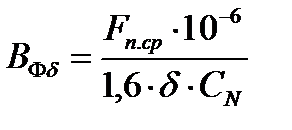
| Тл | 3,427 | 3,386 | 3,052 | 2,631 | 2,021 | 1,915 | |
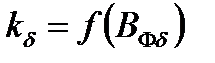
| ----- | 0,66 | 0,68 | 0,72 | 0,75 | 0,87 | 0,88 | |
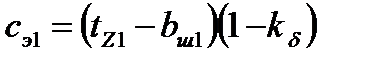
| мм | 3,74 | 3,52 | 3,08 | 2,75 | 1,43 | 1,32 | |
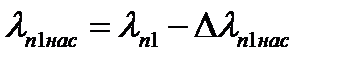
| ----- | 1,29 | 1,3 | 1,32 | 1,335 | 1,412 | 1,42 | |
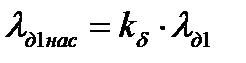
| ----- | 1,162 | 1,197 | 1,267 | 1,32 | 1,531 | 1,549 | |
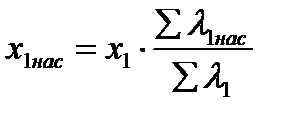
| Ом | 1,084 | 1,094 | 1,112 | 1,127 | 1,187 | 1,192 | |

| ----- | 1,012 | 1,012 | 1,012 | 1,012 | 1,013 | 1,013 | |
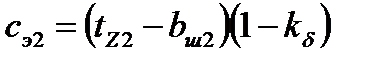
| мм | 5,95 | 5,6 | 4,9 | 4,375 | 2,275 | 2,1 | |
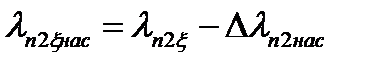
| ----- | 2,263 | 2,268 | 2,279 | 2,288 | 2,355 | 2,364 | |
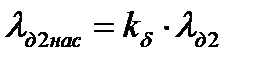
| ----- | 1,135 | 1,17 | 1,238 | 1,29 | 1,496 | 1,514 | |

| Ом | 1,169 | 1,177 | 1,194 | 1,208 | 1,267 | 1,272 | |
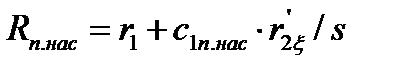
| Ом | 0,694 | 0,739 | 0,9 | 1,629 | 2,861 | 3,1 | |
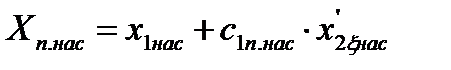
| Ом | 2,267 | 2,285 | 2,321 | 2,35 | 2,47 | 2,48 | |
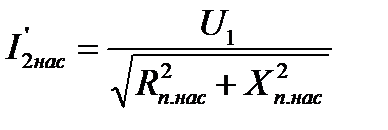
| А | 160,31 | 158,25 | 152,48 | 132,93 | 100,55 | 95,59 | |
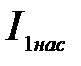
| А | 162,35 | 160,28 | 154,47 | 134,69 | 96,96 | ||
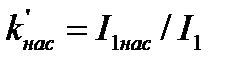
| ----- | 1,156 | 1,155 | 1,14 | 1,105 | 1,042 | 1,036 | |

| ----- | 5,24 | 5,17 | 4,893 | 4,345 | 3,29 | 3,128 | |
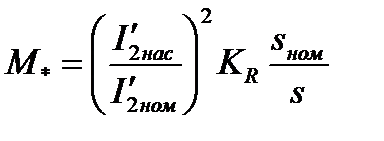
| ----- | 0,783 | 1,9 | 1,189 | 2,14 | 2,42 | 2,4 |
|
|
|
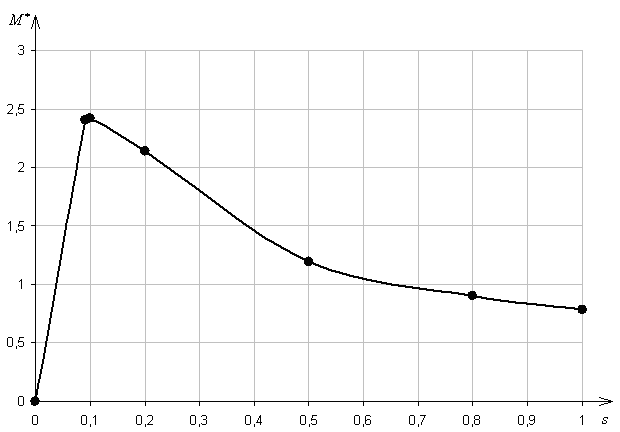
Рис. 14.
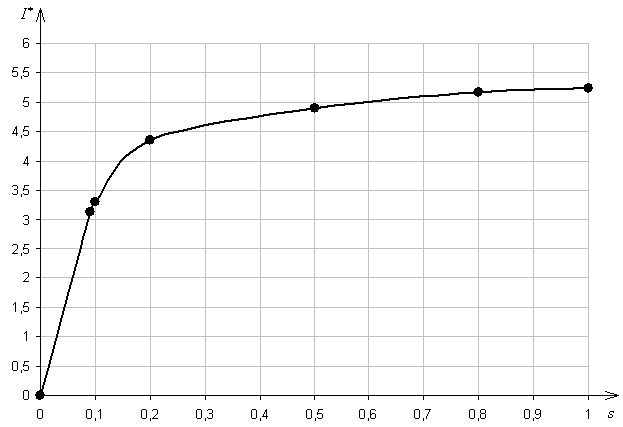
Рис. 15.
Специальная часть.
Список литературы:
1) В.Я. Беспалов, Н.Ф. Котеленец, «Электрические машины»,М.: Академия, 2006 г.
2) И.П. Копылов «Проектирование электрических машин», М.: Энергоатомиздат, 1993г. в 2-х томах.
3) И.П. Копылов «Электрические машины», М.: Высшая школа, 2000 г.
|
|
|


