 |
Классические обратные задачи
|
|
|
|
Содержание
Введение……………………………………………………………………………...3
1. Классические обратные задачи……………………………………………4
2. Постановка, классификация и решение обратных задач динамики…….8
3. Метод квазиобращения…………………………………………………...12
4. Метод разделения искомой системы…………………………………….13
5. Метод проектирования. ………………………………………………….15
6. Задача обеспечение требуемого закона движения………………………16
Заключение………………………………………………………………………….19
Список использованной литературы ……………………………………………..20
Введение
Одной из основных задач динамики механических систем, описываемых обыкновенными дифференциальными уравнениями, является задача определения сил и моментов по заданным кинематическим элементам движения или, в более общей постановке, по заданным свойствам движения. Задачи такого вида с различными их видоизменениями названы обратными задачами динамики, или обратными задачами дифференциальных систем.
Под обратными задачами дифференциальных систем понимаются как задачи о построении силовых полей, так и задачи об определении функционалов, стационаризуемых в процессе движения, о восстановлении и построении уравнений движения механической системы по заданным свойствам ее движения.
Настоящая работа посвящена решению одной из обратных задач обеспечения требуемого закона движения.
Первоначально, Еругиным Н. П. [1] была поставлена и решена задача построения множества уравнений движения системы по заданным интегралам. Данная задача имеет в общем случае неоднозначное решение, в силу некоторых неопределённых функций, что позволяет решать обратные задачи динамики в сочетании с дополнительными требованиями, Галиуллин А.С. и его ученики Мухаметзянов И.А. и Мухарлямов Р.Г. применяют идеи Еругина для построения уравнений программных движений [2, 5].
|
|
|
Для решения рассматриваемой задачи применяется метод квазиобращения [4], который был создан Р. Г. Мухарлямовым. Данный метод является одним из общих методов решения обратных задач динамики в классе обыкновенных дифференциальных уравнений. Также применяются методы разделения и проектирования.
Классические обратные задачи
Под обратными задачами динамики понимается задачи об определении активных сил и моментов, действующих на механическую систему, параметров системы и связей, наложенных на систему, при которых движение с заданными свойствами являются одним из возможных движений рассматриваемой механической системы. Задачи такого вида с различными их видоизменениями названы обратными задачами динамики.
К таким задачам относятся так же [2] как задачи о построении силовых полей по известным свойствам движения материальной точки в этом поле, так и задачи об определении функционалов, стационаризируемых в процессе движения, о восстановлении и построении движения механической системы по заданным свойствам ее движения.
Данное определение отнесено к механическим системам. Однако наряду с механическими системами рассматриваются так же управляемые объекты различной природы (электрической, квантовой, химической и др.). Поэтому содержание обратных задач динамики должно включать определение законов управления движением динамических систем и их параметров из условия осуществления движения по назначенной траектории.
Эти задачи всегда привлекали к себе внимание механиков и математиков, так как они имеют широкие прикладные возможности.
Классическими обратными задачами дифференциальных систем являются:
|
|
|
Задача Ньютона об определении силы, под действием которой планеты совершают движение со свойствами, заданными в виде законов Кеплера;
Задача Бертрана об определении силы, под действием которой материальная точка при любых начальных условиях движется по коническому сечению. Решением задачи Бертрана занимались многие ученые прошлого столетия (В.Г. Имшенецкий,
Ж. Дарбу, Г. Кенигс и др.);
Задача Суслова об отыскании силовой функции, которая определяет силы, вызывающие движение голономной механической системы с задаными интегралами;
Задача Мещерского об определении закона изменения массы точки и скорости изменяющейся массы так, чтобы в заданном поле сил точка переменной массы совершала движение по заданной траектории или по заданному закону;
Задача Гельмгольца о построении функционала, принимающего стационарное значение на решениях заданного обыкновенного дифференциального уравнения второго порядка.
Даинелли в 1880 г. поставил задачу об определении силового поля, для которого заданное семейство кривых 
будет представлять семейство возможных траекторий. Искомое поле сил ищется в следующем виде:
(1.1)
где 
- произвольная функция, 
– компоненты силы, отнесенной к единице массы, в направлении осей координат.
В 1952 г. Н. П. Еругиным была впервые сформулирована обратная задача теории дифференциальных уравнений в виде задачи построения множества систем уравнений по заданным интегралам и указан метод решения этой задачи [1]. В процессе дальнейших исследований оказалось, что метод Еругина позволяет не только построить уравнения движения механической системы по заданным свойствам одного из возможных движений этой системы, но и построить эти уравнения с учетом дополнительных требований, например, устойчивости и оптимальности заданного движения.
В работе [1] была поставлена задача определения множества правых частей систем дифференциальных уравнений
, ( 1.2 )
имеющих заданные функции
(1.3)
своими частными интегралами.
|
|
|
Смысл этой задачи заключается в следующем: если 
- начальное значение вектора 
и 
, то равенство (1.3) должно выполняться при всех 
, где 
- решение уравнения (1.2) при определенной правой части, удовлетворяющее начальному условию и существующее при 
, 
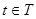или 
.
Условия существования частных интегралов вида (1.3) заключается в том, чтобы
, (1.4)
, 
, 
,
, 
, 
,
, 
, 
.
Равенство (1.4) можно записать в виде линейного алгебраического уравнения относительно 
:
(1.4)*
С 1960 г. А. С. Галиуллин и его ученики И. А. Мухаметзянов и Р. Г. Мухарлямов изучают возможности применения идей Н. П. Еругина для решения обратных задач динамики. Они формируют и рассматривают обратные задачи динамики как задачи построения всего множества дифференциальных уравнений программных движений.
Пусть состояние механической системы определяется векторами обобщенных координат 
и скоростей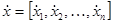 
. Свойства движения механической системы задаются уравнениями связей (в виде многообразия):
(1.5)
правые части которых 
могут быть произвольными постоянными или принимать конкретные значения, в частности, равные нулю. Кроме того, 
, а равенства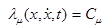 
независимы и совместны в некоторой области фазового пространства 
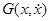при 
.
Согласно методу Еругина, решение различных вариантов постановки обратных задач можно рассматривать в два этапа. На первом этапе заданное многообразие свойств движения (1.5) рассматривается как интегральное многообразие уравнений движения рассматриваемой системы. Поэтому уравнения движения механической системы строятся так, чтобы соотношения 
являлись первыми (
) или частными (
) интегралами этих уравнений. Для этого составляется необходимое и достаточное условие того, что заданные интегралы действительно образуют интегральное многообразие строящейся системы уравнений. Эти условия получаются приравниванием производных заданных интегралов, составленных в силу искомых уравнений, к функциям Еругина, т. е. произвольным функциям, обращающимся в нуль на заданном интегральном многообразии () или просто приравниванием их к нулю (
). Полученные при этом равенства будут необходимыми условиями осуществимости заданного движения для рассматриваемой механической системы.
|
|
|
Второй этап заключается в том, чтобы из построенных таким образом уравнений определить искомые обобщенные силы, параметры системы, а так же дополнительные связи, допускающие движение системы с заданными свойствами.
|
|
|
