 |
Постановка, классификация и решение обратных задач динамики
|
|
|
|
В монографии [2] изложены постановка, классификация обратных задач динамики и их решение в классе обыкновенных дифференциальных уравнений. Галиуллин рассматривает следующие задачи по построению уравнений движения по заданному интегральному многообразию.
1) Основная задача построения уравнений движения.
По заданному интегральному многообразию
(2.1)
построить систему уравнений
(n =1…n) (2.2)
движения механической системы так, чтобы оно являлось одним из ее возможных движений.
2) Восстановление уравнений движения.
По заданному интегральному многообразию
(2.3)
и заданной системе уравнений
(n =1…n) (2.4)
определить вектор-функцию 
параметров системы и дополнительно приложенных к системе силы.
3) Замыкание уравнений движения.
По заданному интегральному многообразию
(2.5)
и заданной системе уравнений
(2.6)
построить систему замыкающих уравнений
(2.7)
так, чтобы система (2.6) – (2.7) представляла собой замкнутую систему.
Искомые функции 
принадлежат классу функций, допускающих существование и единственность решения в некоторой e– окрестности 
заданного многообразия 
.
На первом этапе решения всех типов обратных задач 1) – 3) составляются условия осуществимости движения механической системы с заданными свойствами, которые в общем случае имеют вид
|
|
|
(2.8)
где 
произвольная при 
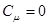функция, такая, что 
и тождественно равная нулю при 
¹0.
Для основной задачи построения уравнений и задачи восстановления уравнения осуществимости движения имеют следующий вид:
(2.9)
где 
- функции Еругина;
и для задачи замыкания условие (2.8) принимает вид:
, (2.10)
где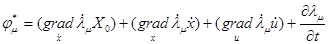 
.
Затем из этих условий определяются правые части уравнений (2.4), (2.7) 
, 
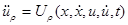соответственно, которые в конечном итоге в векторной форме будут иметь следующий вид:
, (2.11)
где 
определяется из условия
- алгебраическое дополнение (i, j) – го элемента определителя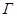 
;
(для задачи замыкания), (2.12)
где 
,
- алгебраическое дополнение 
– го элемента определителя 
и 
определяется из условия
Чтобы определить искомые функции 
в задаче восстановления, необходимо правую часть выражения (2.10) приравнять к известным правым частям заданных уравнений (2.5):
.
Тогда получим следующие равенства:
(n = 1…n) (2.13)
и разрешим данное уравнение относительно функций 
.
Заметим, что поставленная задача имеет в общем случае неоднозначное решение. Во-первых, потому что при m < n условия (2.8) не определяют однозначно все 
, во-вторых, условия (2.8) при 
содержат произвольные функции 
. Все это позволяет решать обратные задачи динамики в сочетании с задачами устойчивости и оптимальности заданного движения, и вообще, в сочетании с дополнительными требованиями относительно динамических показателей движения рассматриваемой механической системы. При этом функции 
будут определять обобщенные силы, возникающие при отклонении движения системы от ее движения с заданными свойствами.
|
|
|
В указанной монографии [2] эта возможность использована для аналитического построения устойчивых систем и систем программного движения в предположении, что движения рассматриваемых материальных систем описываются обыкновенными дифференциальными уравнениями.
Метод квазиобращения.
В настоящее время сформулированы возможные постановки обратных задач дифференциальных систем и разработаны общие методы решения этих задач в классе ОДУ. При этом оказалось, что если заданные свойства движения механической системы могут быть аналитически представлены как первые или частные интегралы соответствующих уравнений движения, то решение обратных задач дифференциальных систем в общем случае сводится к построению дифференциальных уравнений по заданным их интегралам и к определению в дальнейшем из них искомых сил и моментов, параметров и связей, необходимых для осуществления движения рассматриваемой механической системы с предварительно заданными свойствами. Один из общих методов решения 
обратных задач дифференциальных систем в классе ОДУ (метод квазиобращения)
Сущность метода квазиобращения состоит в следующей теореме:
Теорема: Совокупность всех решений линейной системы
, 
, 
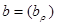, (3.1)
, 
, 
,
в которой матрица А имеет ранг, равный r, определяется выражением
(3.2)
где k – произвольная скалярная величина,
(3.3)
- векторное произведение векторов 
и произвольных векторов 
, 
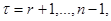
- единичные орты пространства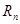 
, 
, 
- матрица, транспонированная к 
.
Прежде всего непосредственной подстановкой можно убедиться в том, что (3.2) удовлетворяет уравнению (3.1). Действительно, произведение 
дает столбец, состоящий из 
нулей, а 
Далее пусть 
некоторое решение уравнения (3.1). Покажем, что оно содержится во множестве (3.2). Представим 
в виде суммы 
где 
вектор, ортогональный 
так что
(3.4)
- вектор, принадлежащий линейному пространству, натянутому на т.е.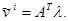 
Тогда из уравнения (3.1) следует, что 
т.е. 
|
|
|
Остается показать, что при определенном выборе матрицы 
первое слагаемое правой части (3.2) совпадает с 
. Для этого положим 
Тогда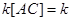 
представляет собой двойное векторное произведение и может быть записано в виде определителя
(3.5)
Поскольку векторы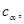 
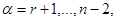произвольны, выберем их так, чтобы векторы 
были линейно независимы и выполнялись равенства
(3.6)
Тогда в силу (3.4), (3.6) в последнем столбце определителя (3.5) все элементы, за исключением , оказываются равными нулю, и (3.5) принимает вид 
где 
- определитель Грама, отличный от нуля.
Следовательно, можно принять 
Тогда 
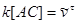и 
.
|
|
|
