 |
Методические указания к заданию 3.1
|
|
|
|
Открытый текст, гамма, криптограмма в криптосистеме с управляемыми операциями представлены четырёхразрядными двоичными операндами (тетрадами), а управляющие сигналы формируются с помощью пяти двоичных разрядов. Ещё один разряд потребуется для формирования сигнала переноса. Таким образом, преобразователь кода должен содержать четыре входа (на них подаётся гамма) и шесть выходов.
Для синтеза преобразователя кода на передающей стороне нужно составить таблицу, которая формируется на основании данных из таблицы 3.1.1. Таблица 4.1.1 составлена для варианта 17
Таблица 4.1.1
| № п/п | Гамма B3B2B1B0 (ABCD) | Операция | Управляющие сигналы S3S2S1S0 | Мod | CN |
| 0 | 0 0 0 0 |
| 0 1 1 0 | 1 | x |
| 1 | 0 0 0 1 | 0 1 1 0 | |||
| 2 | 0 0 1 0 | 0 1 1 0 | |||
| 3 | 0 0 1 1 | 0 1 1 0 | |||
| 4 | 0 1 0 0 |
| 1 0 0 1 | 1 | x |
| 5 | 0 1 0 1 | 1 0 0 1 | |||
| 6 | 0 1 1 0 | 1 0 0 1 | |||
| 7 | 0 1 1 1 | 1 0 0 1 | |||
| 8 | 1 0 0 0 |
| 0 1 1 0 | 0 | 0 |
| 9 | 1 0 0 1 | 0 1 1 0 | |||
| 10 | 1 0 1 0 | 0 1 1 0 | |||
| 11 | 1 0 1 1 | 0 1 1 0 | |||
| 12 | 1 1 0 0 |
| 1 0 0 1 | 0 | 1 |
| 13 | 1 1 0 1 | 1 0 0 1 | |||
| 14 | 1 1 1 0 | 1 0 0 1 | |||
| 15 | 1 1 1 1 | 1 0 0 1 |
В колонке «Гамма» одновременно указаны разряды АЛУ (B3B2B1B0), на которые подаётся гамма, и обозначения этих же разрядов в конверторе Logic Converter (ABCD).
Первые две конки таблицы будут одинаковыми для всех вариантов.
Колонка «Операция» заполняется следующим образом (на примере варианта № 17). В соответствии с таблицей 3.1.1 для гаммы, равной значениям «0», «1», «2», «3», должна выполнятся операция 
, поэтому в строках 0-3 четырежды указана данная операция. Другие строки таблицы заполняются аналогично. Понятно, что в других вариантах последовательность операций будет иной.
Колонка «Управляющие сигналы» заполняется с учётом информации, содержащейся в колонке «Операция». Соответствие управляющих сигналов S3S2S1S0 и выполняемых АЛУ операций следующее:
|
|
|
«» – «0 1 1 0», «
» – «1 0 0 1»,
«
» – «0 1 1 0», «
» – «1 0 0 1»
Входы S3S2S1S0 и Mod предназначены для формирования управляющих сигналов, которые позволяют выбрать одну из тридцати двух возможных операций АЛУ. Напомним, что в данной работе используются лишь четыре операции: две логические операции и две арифметические.
Столбец «Mod» определяет, какую операцию выполняет АЛУ: логическую (значение равно 1) или арифметическую (значение равно 0). Сигнал CN определяет величину переноса. Для логических операций безразлично, какое значение принимает CN, поэтому сигнал обозначен символом «Х». Для арифметического вычитания сигнал CN равен «0», а для арифметического сложения – «1».
На основании данных из таблицы 4.1.1 следует сформировать логические выражения, которые будут использованы для синтеза преобразователя кода. Составить логические выражения проще всего с помощью Logic Converter (логический конвертор).
Для получения математических выражений, описывающих работу ПК, достаточно в конвертор ввести данные из таблицы истинности преобразователя кода. В качестве примера получим выражение для S3 (вариант 17). Логические выражения формируются при нажатии кнопки SIMP, находящейся в поле Conversions.
Как видно из приведённого рисунка, вся введённая в конвертор таблица истинности описывается одним символом В. Анализируя таблицу 4.1.1, несложно заметить, что сигналы на шинах S3 и S0 должны совпадать, поэтому эти два входа АЛУ должны быть соединены между собой.
Учитывая последовательность ввода операндов и принятые обозначения (см. табл. 4.1.1), можно записать: S3 = S0 = B2.
Фрагмент схемы ПК, который реализует полученное выражение показан на рисунке.
Напомним, что символ А в окне Logic Converter соответствует разряду гаммы В3, символ В – В2, С – В1, D – В0.
Описанные действия по определению сигнала на одном выходе ПК следует повторить для всех выходов ПК. В результате должно быть получено шесть логических выражений, часть из которых могут быть одинаковыми.
|
|
|
Например, анализируя таблицу 4.1.1, легко заметить, что сигналы 
. Это означает, что эти шины должны быть соединены между собой.
Ниже приведены результаты формирования логических выражений для остальных четырёх выходных сигналов первого ПК:
, 
, 
.
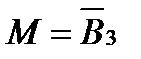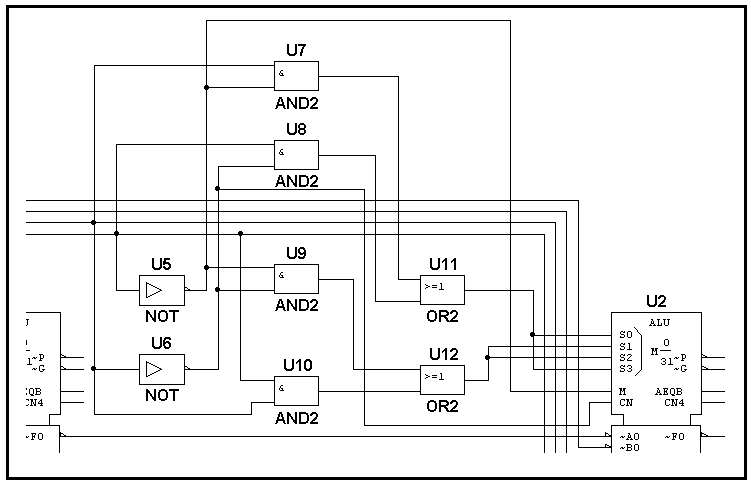
Эти выражения следует использовать для построения схемы преобразователя кода на передаче. Вся схема будет состоять из двух инверторов для сигналов В1 и В3. Ещё один выходной сигнал ПК берётся непосредственно с шины В2. На рисунке показана шифрующая часть криптосистемы (передающая часть).
Затем следует выполнить синтез ПК на приёмной стороне. Для этого, используя данные таблицы 3.1.1, нужно составить новую таблицу истинности. При этом следует помнить, что логические операции на приёме и передаче должны совпадать, а арифметические операции на приёме должны поменяться на противоположные, то есть, если на передаче использовалось арифметическое сложение, то на приёме нужно использовать арифметическое вычитание, и наоборот. В итоге таблица истинности примет следующий вид:
Таблица 4.1.2
| № п/п | Гамма B3B2B1B0 (ABCD) | Операция | Управляющие сигналы S3S2S1S0 | Мod | CN |
| 0 | 0 0 0 0 |
| 0 1 1 0 | 1 | x |
| 1 | 0 0 0 1 | 0 1 1 0 | |||
| 2 | 0 0 1 0 | 0 1 1 0 | |||
| 3 | 0 0 1 1 | 0 1 1 0 | |||
| 4 | 0 1 0 0 |
| 1 0 0 1 | 1 | x |
| 5 | 0 1 0 1 | 1 0 0 1 | |||
| 6 | 0 1 1 0 | 1 0 0 1 | |||
| 7 | 0 1 1 1 | 1 0 0 1 | |||
| 8 | 1 0 0 0 |
| 1 0 0 1 | 0 | 1 |
| 9 | 1 0 0 1 | 1 0 0 1 | |||
| 10 | 1 0 1 0 | 1 0 0 1 | |||
| 11 | 1 0 1 1 | 1 0 0 1 | |||
| 12 | 1 1 0 0 |
| 0 1 1 0 | 0 | 0 |
| 13 | 1 1 0 1 | 0 1 1 0 | |||
| 14 | 1 1 1 0 | 0 1 1 0 | |||
| 15 | 1 1 1 1 | 0 1 1 0 |
Используя логический конвертор и данные из таблицы, несложно получить выражения, которые описывают ПК на приёмной стороне:
,
,
, 
.
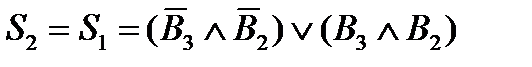На основе этих выражений формируется схема ПК на приёмной стороне. Следующий рисунок показывает схему второго ПК.
Полная принципиальная схема криптосистемы имеет вид:
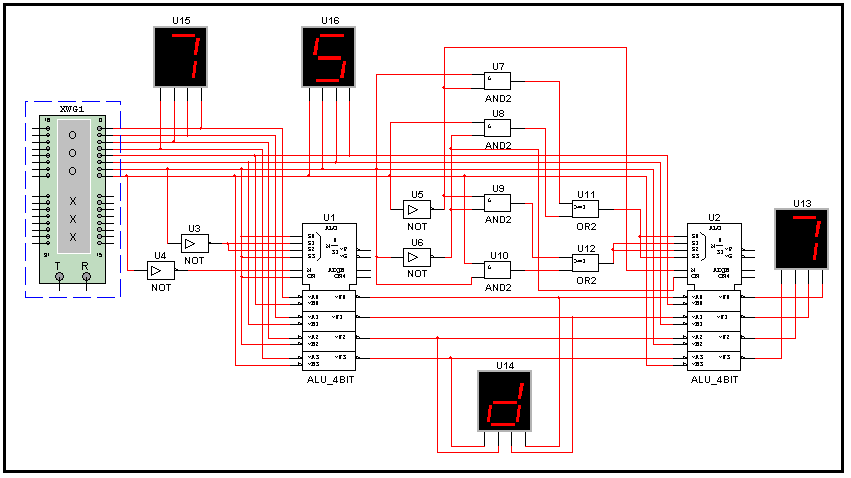
Четырёхбитный открытый текст подаётся на вход А первого арифметико-логического устройства (U1). Гамма подаётся на вход В. Вид выполняемой операции задаётся с помощью преобразователя кода (U3, U4). Криптограмма формируется на выходе F первого АЛУ (U1). Дешифрация криптограммы осуществляться на приёмной стороне с помощью второго АЛУ (U2). Вид выполняемой операции синхронно изменяется под управлением гаммы. Принятый открытый текст появлялся на выходе F второго АЛУ (U2).
|
|
|
Исходный текст, принятый текст, гамма и криптограмма отображаются с помощью четырёх индикаторов соответственно U15, U13, U16, U14. Значения гаммы и передаваемый текст формируются с помощью генератора слов XWG1 (Word Generator). На рисунке показан генератор слов, в буфере которого содержатся данные для варианта 17.
Как видно из рисунка, выполняется 6-я по счету операция. В соответствии с таблицей 4.1.2 в этот момент времени выполняется шифрующая операция «Равнозначность». Операция выполняется над числами 5 и 7 и результат равен шестнадцатеричному числу D. На приёмной стороне число подвергается расшифрованию и в результате получается число 7 (открытый текст). Именно эти числа показаны на принципиальной схеме криптосистемы.
На последнем этапе выполнения лабораторной работы следует проверить правильность работы созданной криптосистемы. Для этого в окне свойств генератора слов XWG1 нужно выставить заданные значения гаммы и открытого текста, как показано на рисунке, и нажатием на клавишу Step, проверить все операции. Для удобства флажок таблицы исчисления должен стоять на отметке Hex.
Результаты ручных расчётов и моделирования криптосистемы следует внести в таблицу 3.1.3.
В рассмотренном примере синтеза криптосистемы принципиальные схемы преобразователей кодов достаточно просты. При существенном усложнении конструкции возникает проблема из-за высокой плотности размещения микросхем на отведённой площади листа. Увеличить пространство рабочего стола можно с помощью диалогового окна, показанного на следующем рисунке. Вызывается диалоговое окно с помощью контекстного меню и выбора опции Properties (Свойства).
Как и всякая имитация, рассмотренная модель не полностью соответствует реальной криптографической системе. Например, при моделировании предполагается, что соединение между передающей и приёмной сторонами происходит по четырём проводам. В реальной криптосистеме связь должна осуществляться по двухпроводной линии.
|
|
|
Кроме того, при моделировании считается, что операнды, циркулирующие в криптосистеме, являются четырёхразрядными целыми числами. Диапазоны изменения чисел составляли 
и 
. Заметим, что в реальной криптосистеме при формировании криптограммы возможно использование не только целых, но и вещественных чисел.
Требования к отчёту
Отчёт подготавливается в электронном виде. Он должен содержать постановки задач, скриншоты, которые показывают порядок решения задач, схемы, таблицы с результатами моделирования, необходимые комментарии и анализ полученных результатов.
6. Контрольные вопросы
6.1. В чём состоит основная идея шифрования с помощью управляемых операций?
6.2. Выполните операцию вычитания в дополнительном коде.
6.3. Запишите закон де Моргана.
6.4. Перечислите возможности прибора Logic Converter –XLC1.
6.5. Составьте таблицу истинности логического элемента ИЛИ-НЕ
6.6. Составьте таблицу истинности логического элемента И-НЕ.
6.7. Запишите тождества алгебры логики.
6.8. Запишите законы алгебры логики.
6.9. Как представить отрицательное число в дополнительном коде?
6.10. Чем отличаются логические и арифметические операции?
6.11. Для чего используются в АЛУ выводы M и CN?
6.12. Какие преимущества шифра с управляемыми операциями по сравнению с аддитивным шифром?
6.13. Что определяет вид выполняемой операции для каждого обрабатываемого сомвола?
6.14. Какие логические и арифметические операции использованы в рассмотренном шифре?
Лабораторная работа № 18
Сжатие информации
Цель работы
Изучить метод сжатия информации RLE, получить практические навыки сжатия файлов стандартными архиваторами.
Общие сведения
Несмотря на то, что объёмы внешней памяти ЭВМ постоянно растут, потребность в сжатии информации не уменьшается. Это объясняется тем, что сжатие необходимо не только для экономии места в памяти ЭВМ, но и для быстрой передачи информации по Сети (например, для трансляции спортивного соревнования в реальном масштабе времени).
Кроме того, возможность отказа магнитных и полупроводниковых носителей информации, разрушающее действие вирусов заставляют пользователей делать резервное копирование ценной информации на другие (запасные) носители информации. Очевидно, что разумнее информацию хранить сжатой.
Сжатие информации (архивация) — это такое преобразование информации, при котором объем (размер) файла уменьшается, а количество информации, содержащейся в архиве, остаётся прежним.
Степень сжатия информации зависит от содержимого файла и формата файла, а также от выбранного метода сжатия информации. Степень (качество) сжатия файлов характеризуется коэффициентом сжатия Kc, определяемым как отношение объёма исходного файла Vo к объёму сжатого файла Vc:
|
|
|
Чем больше величина Kc, тем выше степень сжатия информации.
Все существующие методы сжатия информации можно разделить на два класса: сжатие без потерь информации (обратимый алгоритм) и сжатие с потерей информации (необратимый алгоритм). В первом случае исходную информацию можно точно восстановить по имеющейся упакованной информации. Во втором случае распакованное сообщение (например, фотография) будет незначительно отличаться от исходного сообщения.
Одна из идей сжатия состоит в учёте того факта, что в файлах часто встречаются несколько подряд идущих одинаковых байтов, а некоторые последовательности байтов повторяются многократно. При архивации такие места файла можно заменить командами вида «повторить данный байт n раз» или «взять часть данных длиной k байтов, которая встречалась m байтов назад». Такой алгоритм архивации называется методом сжатия информации RLE (R un L ength E ncoding — кодирование путём учёта повторений или кодирование длин серий).
Рассмотрим основную идею сжатия информации методом RLE.
Упакованная методом RLE последовательность состоит из управляющих байтов, за которыми следуют один или несколько байтов данных. При этом, если старший бит управляющего байта равен 1, то следующий за ним байт данных нужно повторить при декодировании столько раз, сколько указано в оставшихся 7 битах управляющего байта.
Например, управляющий байт 10001001 говорит, что следующий за ним байт нужно повторить 9 раз, так как 10012 = 910.
Если старший бит управляющего байта равен 0, то при декодировании нужно взять несколько следующих байтов без изменений. Число байтов, которые берутся без изменений, указывается в оставшихся 7 битах. Например, управляющий байт 00000011 говорит, что следующие за ним 3 байта нужно взять без изменений.
Рассмотрим пример сжатия данных методом RLE.
Пусть дана некоторая последовательность из 12 байтов:
11111111 11111111 11111111 11111111 11111111 11110000
00001111 11000011 10101010 10101010 10101010 10101010.
В начале исходной двоичной последовательности 5 раз повторяется байт 11111111. Чтобы упаковать эти 5 байтов, нужно записать сначала управляющий байт 10000101, а затем повторяемый байт 11111111. В результате сжатия этого фрагмента данных выигрыш составит 3 байта. Далее идут 3 разных (неповторяющихся) байта: 11110000 00001111 и 11000011. Чтобы их «упаковать», нужно записать управляющий байт 00000011, а затем указать эти 3 неповторяющихся байта. В результате архивации этого фрагмента двоичной последовательности получается увеличение объёма архива по сравнению с исходными данными на 1 байт. Далее в последовательности 4 раза повторяется байт 10101010. Для архивации этого фрагмента двоичных данных нужно сформировать управляющий байт 10000100 и записать один раз повторяемый байт 10101010. Сжатие последнего фрагмента даст выигрыш 2 байта.
В результате проведённой архивации получена новая последовательность данных (архив), состоящая из 8 байтов:
10000101 11111111 00000011 11110000
00001111 11000011 10000100 10101010.
Таким образом, 12 байт исходной двоичной последовательности удалось сжать до 8 байт. Коэффициент сжатия составил:
|
|
|
