 |
Дифференциальные исчисления функций одной переменной
|
|
|
|
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Кировский филиал
Федерального государственного бюджетного образовательного учреждения
Высшего профессионального образования
«Московский государственный университет путей сообщения»
(Кировский филиал МИИТ)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Для реализации программы дисциплины
«Прикладная математика»
Контрольная работа №1
для специальности
270835 Строительство железных дорог, путь и путевое хозяйство
заочное отделение
базовая подготовка среднего профессионального образования
(приложение к программе)
Киров
Методические указания выполнения контрольной работы для реализации программы дисциплины «Математика» для студентов заочного отделения рассмотрены и одобрены на заседании цикловой комиссии общепрофессиональных и математических дисциплин Кировского филиала МИИТ
Протокол № от ___________20 г.
Председатель ЦК
_______________________ Малышева Э.Ф.
Автор методических указаний для реализации программы дисциплины «Математика» по выполнению контрольной работы для студентов заочного отделения – преподаватель Кировского филиала МИИТ
Рязанова М.В. _______________
(дата, подпись)
Внутренний рецензент методических указаний для реализации программы дисциплины «Математика» по выполнению контрольной работы для студентов заочного отделения - преподаватель Кировского филиала МИИТ
Фоминых В.В. ______________
(дата, подпись)
Пояснительная записка.
Учебная дисциплина «Математика» является естественнонаучной, формирующей базовые знания для освоения общепрофессиональных и специальных дисциплин.
|
|
|
После изучения материала каждого раздела студент должен выполнить домашнюю контрольную работу. Контрольная работа выполняется в отдельной тетради. Условие задачи переписывается полностью. Решение примеров сопровождается краткими и чёткими пояснениями.
Для подготовки к зачёту необходимо ответить на вопросы, которые указаны в конце методических рекомендаций.
КОНТРОЛЬНАЯ РАБОТА
| Две последние цифры шифра | Номер варианта | Номера задач | Две последние цифры шифра | Номер варианта | Номера задач | ||
| 3;34;65;96;127 | 28;59;90;91;122 | ||||||
| 4;35;66;97;128 | 29;60;61;92;123 | ||||||
| 5;36;67;98;129 | 30;31;62;93;124 | ||||||
| 6;37;68;99;130 | 1;32;63;94;125 | ||||||
| 7;38;69;100;131 | 2;33;64;95;126 | ||||||
| 8;39;70;101;132 | 5;37;69;102;134 | ||||||
| 9;40;71;102;133 | 8;40;73;105;137 | ||||||
| 10;41;72;103;134 | 11;43;76;108;140 | ||||||
| 11;42;73;104;135 | 14;47;79;111;143 | ||||||
| 12;43;74;105;136 | 17;50;82;114;147 | ||||||
| 13;44;75;106;137 | 20;53;85;117;150 | ||||||
| 14;45;76;107;138 | 23;56;88;120;124 | ||||||
| 15;46;77;108;139 | 26;59;62;95;127 | ||||||
| 16;47;78;109;140 | 29;33;65;98;130 | ||||||
| 17;48;79;110;141 | 2;36;68;101;133 | ||||||
| 18;49;80;111;142 | 5;39;71;104;137 | ||||||
| 19;50;81;112;143 | 8;42;74;107;140 | ||||||
| 20;51;82;113;144 | 11;45;77;110;143 | ||||||
| 21;52;83;114;145 | 15;49;81;116;152 | ||||||
| 22;53;84;115;146 | 19;52;84;119;159 | ||||||
| 23;54;85;116;147 | 22;57;89;92;121 | ||||||
| 24;55;86;117;148 | 27;31;75;97;128 | ||||||
| 25;56;87;118;149 | 30;34;81;99;131 | ||||||
| 26;57;88;119;150 | 6;35;86;106;136 | ||||||
| 27;58;89;120;121 | 7;38;72;112;153 |
Методические указания
|
|
|
Комплексные числа.
Числа вида  , где
, где  – действительная,
– действительная, 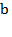 ‒ мнимая части комплексного числа и
‒ мнимая части комплексного числа и  и
и  действительные числа, называются комплексными числами.
действительные числа, называются комплексными числами.  называют действительной частью (обозначают
называют действительной частью (обозначают  ), а
), а 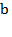 ‒ мнимой частью (обозначают
‒ мнимой частью (обозначают  ) комплексного числа.
) комплексного числа.
В электротехнике, где буква  обозначает ток, мнимую единицу обозначают буквой
обозначает ток, мнимую единицу обозначают буквой  .
.
Если операции сложения, вычитания и умножения комплексных чисел соответствуют обычным правилам раскрытия скобок, то для выполнения деления нужно умножать числитель и знаменатель дроби на число, сопряженное знаменателю.
Пример 1. Пусть  ,
,  . Тогда:
. Тогда:
 ,
,
 ,
,
 ,
,
 ,
,

На множестве комплексных чисел можно решать квадратные уравнения, дискриминант которых отрицательный.
Пример 2. Решите уравнение  .
.
Находим дискриминант: 
Находим корни:  ,
, 
Изображение комплексных чисел. Модуль и аргумент комплексного числа
 Рассмотрим на плоскости декартову прямоугольную систему координат
Рассмотрим на плоскости декартову прямоугольную систему координат  . Каждому комплексному числу
. Каждому комплексному числу  можно сопоставить точку с координатами
можно сопоставить точку с координатами  , и наоборот, каждой точке с координатами
, и наоборот, каждой точке с координатами  можно сопоставить комплексное число
можно сопоставить комплексное число  . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.
. Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.
 Пример 3. Изобразим на комплексной плоскости числа
Пример 3. Изобразим на комплексной плоскости числа  ,
,  ,
,  ,
,  ,
,  .
.
Однако чаще комплексные числа изображают в виде вектора с началом в точке 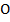 , а именно, комплексное число
, а именно, комплексное число  изображается радиус-вектором точки с координатами
изображается радиус-вектором точки с координатами  . В этом случае изображение комплексных чисел из предыдущего примера будет таким:
. В этом случае изображение комплексных чисел из предыдущего примера будет таким:
 Пусть комплексное число
Пусть комплексное число  изображается радиус-вектором. Тогда длина этого вектора называется модулем числа
изображается радиус-вектором. Тогда длина этого вектора называется модулем числа  и обозначается
и обозначается 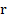 или
или  . Из рисунка очевидно, что
. Из рисунка очевидно, что 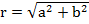 .
.
Угол, образованный радиус-вектором числа  с осью
с осью  , называется аргументом числа
, называется аргументом числа  и обозначается
и обозначается 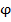 или
или 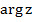 . Аргумент числа определяется не однозначно, а с точностью до числа, кратного
. Аргумент числа определяется не однозначно, а с точностью до числа, кратного  . Обычно аргумент указывают в диапазоне от
. Обычно аргумент указывают в диапазоне от  до
до  . Кроме того у числа
. Кроме того у числа  аргумент не определен.
аргумент не определен.
Величину угла 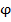 можно найти двумя способами:
можно найти двумя способами:
I. Из системы уравнений 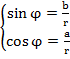 ,
,
II формуле 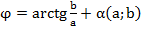 , где
, где 
Тригонометрическая и показательная форма комплексного числа
|
|
|
Тригонометрическая и показательная формы ‒ это указание числа по двум его характеристикам: модулю и аргументу.
 ‒ тригонометрическая форма,
‒ тригонометрическая форма,
 ‒ комплексная форма.
‒ комплексная форма.
Замечание. При записи числа в тригонометрической форме НЕЛЬЗЯ вычислять значения  и
и 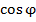 , иначе мы потеряем явное указание аргумента
, иначе мы потеряем явное указание аргумента  и снова вернемся к алгебраической форме. Кроме того, если угол
и снова вернемся к алгебраической форме. Кроме того, если угол 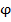 получился отрицательным, то знак
получился отрицательным, то знак  НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ убирать его под знаком косинуса.
НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ убирать его под знаком косинуса.
Для отыскания аргумента (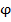 ) используют таблицу 1.
) используют таблицу 1.
Таблица 1.

| 
| 
| 
| 
| 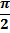
| 
| 
| 
| 
| 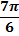
| 
| 
| 
| 
| 
| 
| 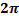
|

| 
| 
| 
| 
| 
| 
| 
| 
| 
| ‒1 | 
| 
| 
| ||||

| 
| 
| 
| 
| 
| 
| ‒1 | 
| 
| 
| 
| 
| 
| ||||

| 
| 
| 
| 
| ‒1 | 
| 
| 
| 
| 
| ‒1 | 
| |||||

| 
| 
| 
| 
| ‒1 | 
| 
| 
| 
| 
| ‒1 | 
| 
|
Пример 4. Записать комплексные числа 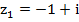 ,
,  ,
,  ,
, 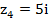 ,
,  в тригонометрической и показательной форме.
в тригонометрической и показательной форме.
Решение. Запишем числа со строгим указанием действительной и мнимой части:
 ,
,  ,
,  ,
, 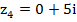 ,
, 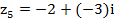 .
.
Находим модуль и аргумент у каждого числа:
 ,
, 
 ,
, 
 ,
, 
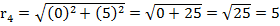 ,
, 
 ,
,  табличного значения нет, поэтому для определения аргумента воспользуемся вторым способом.
табличного значения нет, поэтому для определения аргумента воспользуемся вторым способом.  , так как
, так как  то
то  . Получаем
. Получаем  .
.
 ,
,  ,
,
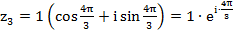 ,
,  ,
, 
Возведение в степень комплексного числа. Извлечение корня из комплексного числа
Для возведения комплексных чисел в степень используют формулу Муавра: 
Пример 5. Вычислите  , если z
, если z  .
.
Решение. Находим тригонометрическую форму числа  :
:
 ,
,  , z
, z 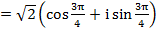
По формуле Муавра

Можно представить данное комплексное число в алгебраической форме

Для извлечения корня из комплексного числа используют формулу
 где
где  .
.
Извлечение квадратного корня из комплексного числа  . Пусть
. Пусть  , где
, где  и
и 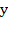 – действительные числа. Возводя обе части этого равенства в квадрат, получаем
– действительные числа. Возводя обе части этого равенства в квадрат, получаем
 .
.
Что равносильно системе 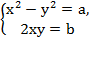 .
.
Решая эту систему, получаем:  ,
,  .
.
Таким образом, извлечение корня квадратного из комплексного числа осуществляется по формуле
 .
.
В скобках перед мнимой единицей берется знак плюс, если  , и знак минус, если
, и знак минус, если  .
.
Пример 5. Найдите  , если
, если  .
.
Решение. Запишем число  . в тригонометрической форме:
. в тригонометрической форме:
|
|
|
 ,
,  ,
, 
Тогда  где
где 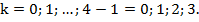
При  получим:
получим: 
При  получим:
получим: 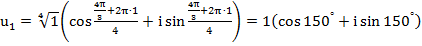
При 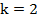 получим:
получим: 
При  получим:
получим: 
Пример 6. Решите уравнение  .
.
Решение. Находим дискриминант:  .
.
Найдем  ,
,  , так как
, так как  то в скобках перед мнимой единицей берем знак плюс. Следовательно
то в скобках перед мнимой единицей берем знак плюс. Следовательно  .
.
Теперь находим корни квадратного уравнения

Дифференциальные исчисления функций одной переменной
Функция  описывает зависимость между двумя переменными величинами
описывает зависимость между двумя переменными величинами  и
и  . Если независимая переменная
. Если независимая переменная  в точке
в точке  получила приращение
получила приращение  (т.е.
(т.е. 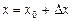 ), то переменная
), то переменная  получит приращение
получит приращение 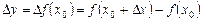 .
.
Предел отношения 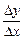 , если
, если  стремится к нулю, называется производной функции
стремится к нулю, называется производной функции  в точке
в точке  и обозначается
и обозначается  или
или 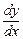 .
. 

Операция нахождения производной функции называется дифференцированием. Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке.
|
|
|


