 |
Почти у всех задач критерии написаны на основании «приведенного» к задаче решения. В случае «другого» решения нужно выработать другие критерии в соответствии с общими требованиями к критериям.
|
|
|
|
РЕШЕНИЯ ЗАДАЧ 9 КЛАСС
Общие замечания по проверке:
Почти у всех задач критерии написаны на основании «приведенного» к задаче решения. В случае «другого» решения нужно выработать другие критерии в соответствии с общими требованиями к критериям.
1. Существует ли 2012 целых чисел произведение которых равно двум, а сумма равна нулю?
Ответ: не существует.
Решение. Поскольку произведение целых чисел равно 2, то одно из этих чисел (если они существуют) должно равняться ±2, а остальные 2011 равны ±1. Но сумма 2011 нечётных чисел и одно чётного является нечётной и значит не равна нулю. Противоречие.
Критерии проверки. Из равенства произведения двум сделан вывод что одно чётное а, остальные нечётные, но противоречие не указано: 2 балла.
2. Мистер Твистер хочет купить завод, газету и пароход. Если он купит только завод, то у него останется 3 млн. долларов. Если он купит пароход, то у него останется 4 млн. долларов. Если же он купит газету, то у него останется 8 млн. долларов. Хватит ли денег у Мистера Твистера, чтобы купить одновременно завод, газету и пароход?
Ответ: Не сможет.
Решение. Пусть завод стоит z млн. долларов, газета стоит g млн. долларов, пароход стоит p млн. долларов, а у мистера Твистера имеется S млн. долларов. Тогда условия задачи можно записать так S–z=3, S–p=4, S–g=8. Если у него не хватит денег на покупку завода, газеты и парохода, то z+g+p>S. Это неравенство равносильно следующему S–3+S–4+S–8>S или S>7,5, что верно, так как после покупки газеты у него остается 8 млн. долларов. А это значит, что он не сможет купить одновременно завод, пароход и газету.
Критерии проверки. Составлены три уравнения и неравенство, но верность неравенства не обоснована: 2 балла.
|
|
|
3. Пусть ABC - остроугольный треугольник. Прямая параллельная стороне BC пересекает стороны AB и AC в точках D и E соответственно. Окружность описанная около треугольника ADE пересекает отрезок CD в точке F отличной от точки D. Доказать, что треугольники AFE и CBD подобны.
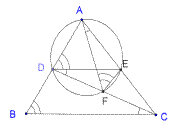Решение. Поскольку прямые DE и BC параллельны, то ÐDCB = ÐCDE, кроме того углы вписанные в одну окружность и опирающиеся на одну дугу равны: ÐFDE = ÐFAE, значит ÐDCB = ÐCDE = ÐFDE =ÐFAE. Аналогично ÐABC = ÐADE = ÐAFE. Таким образом в этих треугольниках имеется по два равных угла и значит они подобны.
4. Числа x 1, x 2, x 3, …, x 2012 принадлежат промежутку [0;1]. Доказать неравенство
x 1 x 2 x 3 … x 2012 + (1– x 1) (1– x 2) (1– x 3) … (1– x 2012) £ 1.
При каких значениях x 1, x 2, x 3, …, x 2012 может достигаться равенство?
Ответ: Равенство достигается при
x 1= x 2= x 3=…= x 2012 =1,или x 1= x 2= x 3=…= x 2012 =0,
Решение. Если число m лежит в промежутке [0;1], то и число 1– m тоже лежит в этом промежутке, а также произведение чисел из этого промежутка также ему принадлежит и поскольку для любых двух чисел a и b из промежутка [0;1] выполняется неравенство ab ≤ a, то
x 1 x 2 x 3 … x 2012 + (1– x 1) (1– x 2) (1– x 3) … (1– x 2012) £ x 1 + 1– x 1 = 1.
Неравенство обращается в равенство только при указанных в ответе значениях.
Критерии проверки. Не указаны условия равенства минус один балл.
5. Даны 10 точек, являющихся вершинами выпуклого десятиугольника. Какое наибольшее число треугольников с вершинами в этих точках можно выбрать таким образом, чтобы каждый треугольник имел сторону, не являющуюся стороной других выбранных треугольников?
Ответ: 9´8/2 = 36.
Решение. Пример, когда треугольников именно столько, получается, если рассмотреть все треугольники с вершиной в данной точке А: у каждого из них сторона, противолежащая вершине А, уникальна, т.е. не входит ни в какой другой из них. Покажем, что большего числа треугольников выбрать не удастся. Каждый отрезок с концами в данных точках входит в 8 треугольников с вершинами в данных точках. Всего отрезков с концами в данных 10 точках имеется 10´9/2 = 45. Если выбрано больше 36 треугольников, то неуникальных сторон будет не больше, чем 45 – 37 = 8, и каждая считается в составе выбранных треугольников не больше 8 раз. Поэтому всего у выбранных треугольников должно быть не больше 8´8+37 = 101 сторон. Однако, на самом деле их 3´37 = 111. Противоречие.
|
|
|
Составитель всех задач 9 класса Р.Г. Женодаров
РЕШЕНИЯ ЗАДАЧ 10 КЛАСС
Общие замечания по проверке:
Почти у всех задач критерии написаны на основании «приведенного» к задаче решения. В случае «другого» решения нужно выработать другие критерии в соответствии с общими требованиями к критериям.
1. Доказать, что если уравнения
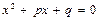и 
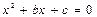
не имеют корней, то уравнение
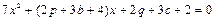
тоже не имеет корней.
Решение. Так как уравнения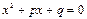 
и 
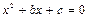не имеют корней, то 
и 
для любых x.
Заметим, что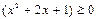 
для всех x. Тогда
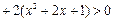для любых x.
2. Наименьшее общее кратное семи натуральных чисел равно 2012. Найдите наименьшую возможную сумму этих чисел.
Решение. Разложим число 2012 на простые множители 
Одно из чисел, НОК которых равен 2012, должно делиться на 
, и одно (возможно то же самое) – на 503. Если одно и то же число кратно и 4, и 503, то оно кратно 2012, а сумма семи чисел не меньше 2018. Если 4 и 503 кратны разные числа, то сумма всех семи чисел не меньше 4+503+1+1+1+1+1=512. Поскольку НОК(4,503,1,1,1,1,1)=2012, то 512 и есть наименьшее возможное значение суммы.
Комментарии по проверке:
При доказательстве минимальности рассмотрен только случай, когда 4 и 503 кратны разные числа – 2 балла.
Приведен пример чисел, с суммой 512, но нет доказательства минимальности – 3 балла.
Доказано, что сумма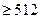 
, но не указан пример таких чисел – 4 балла.
3. Три прямые пересекаются в одной точке O. Вне этих прямых взяли точку M и опустили из нее перпендикуляры на них. Точки H1, H2 и H3 – основания этих перпендикуляров. Найдите отношение длины отрезка OM к радиусу окружности, описанной около треугольника H1H2H3.
Ответ: 2.
Решение.
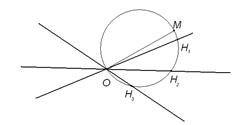Рассмотрим сначала две пересекающиеся прямые и точку М, лежащую вне этих прямых. Н 1 и Н 2 – основания перпендикуляров, опущенных из точки М на эти прямые. Возможны случаи:
|
|
|
1) Н 1 и Н 2 лежат по разные стороны от прямой ОМ;
2) Н 1 и Н 2 лежат по одну сторону от прямой ОМ;
3) Н 1 или Н 2 совпадает с точкой О.
В первом случае Ð МН 1 О +Ð МН 2 О = 90º+90 º =180º. Четырехугольник МН 1 ОН 2 является вписанным, т.е. точки М, Н 1, О и Н 2 лежат на одной окружности, причем диаметр этой окружности – отрезок ОМ. Во втором случае четырехугольник МН 1 Н 2 О является вписанным. Точки М, Н 1, О и Н 2 снова лежат на одной окружности с диаметром ОМ. В третьем случае, очевидно, для точек М, Н 1, О и Н 2 получаем то же самое.
Проведем третью прямую и отметим точку Н 3. Тогда, очевидно, точки Н 1, Н 2 и Н 3 лежат на окружности с диаметром ОМ и искомое отношение равно 2.
Комментарии по проверке:
Задача решена, но при доказательстве того, что М, Н 1, О и Н 2 лежат на одной окружности рассмотрен только случай 1) или случай 2) – 5 баллов.
4. Пять корней многочлена 
образуют возрастающую геометрическую прогрессию. Найдите знаменатель этой прогрессии.
Ответ: 
.
Решение. Обозначим знаменатель прогрессии q, q >1. Пусть корни многочлена x 1, x 2, x 3, x 4и x 5равны соответственно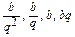 
и 
.
Воспользуемся теоремой Виета для многочлена пятой степени.
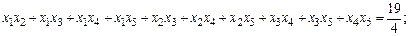
Обозначим 
. Тогда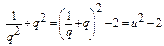 
.
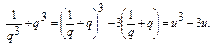
Получим: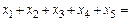 
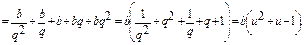
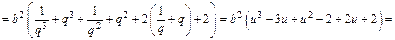
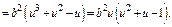
Получим систему:
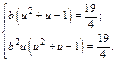
Значит,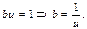 
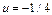или 
.
Для 
получаем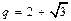 
или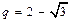 
. Так как прогрессия возрастающая, то 
.
Комментарии по проверке:
Правильно составлена система двух уравнений, неизвестными в которой являются знаменатель прогрессии и какой-то из ее членов, но при этом она не решена или решена неверно – 2 балла.
5. В анкете 2012 вопросов, на каждый из которых - два варианта ответа: «да» или «нет». Назовем двух людей “похожими”, если они ответили одинаково не менее чем на половину вопросов. Докажите, что среди любых 1007 человек найдутся “похожие” люди.
Решение. Докажем методом от противного. Предположим, что найдутся 1007 попарно непохожих людей. Для пары анкет различие в ответе на один вопрос назовем «нюансом». Оценим общее количество «нюансов» для всех пар людей, которые можно составить из наших 1007 непохожих. Всего пар 
. Для каждой пары не менее 1007 «нюансов». Всего получаем не менее 
« нюансов».
|
|
|
Теперь рассмотрим один конкретный вопрос. Пусть на него k человек ответили «да». Тогда 1007- k ответили «нет». Тогда из-за этого вопроса образуется k (1007- k) «нюансов».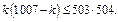 
Всего вопросов 2012, поэтому общее число «нюансов»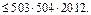 
Но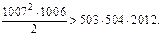 
Противоречие!
Комментарии по проверке: Правильно получена только одна из оценок на общее количество «нюансов» для 1007 непохожих людей: верхняя или нижняя – 2 балла.
Составитель всех задач 10 класса К.П. Исаев
РЕШЕНИЯ ЗАДАЧ 11 КЛАСС
Общие замечания по проверке:
|
|
|
