Почти у всех задач критерии написаны на основании «приведенного» к задаче решения. В случае «другого» решения нужно выработать другие критерии в соответствии с общими требованиями к критериям.

Класс

 

1. Известно, что квадратные трехчлены и и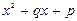меют различные действительные корни. Рассмотрим всевозможные парные произведения корней первого квадратного трехчлена на корни второго (всего таких произведений четыре). Докажите, что сумма обратных величин данных произведений не зависит от p и q.

Решение. Пусть x ₁, x ₂ – корни первого трехчлена и x ₃, x₄, тогда необходимо доказать, что 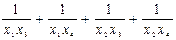не зависит от p и q. Преобразуем данное выражение:

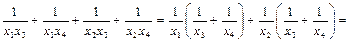
По теореме Виета имеем: и

Тогда .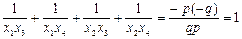

 

2. Числа tg x, tg 2x, tg 3x, являются членами геометрической прогрессии. Найдите знаменатель прогрессии.

Ответ: .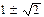

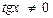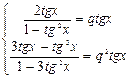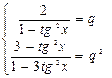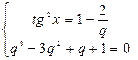Решение. Так как числа являются членами геометрической прогрессии, то и Û Û Û Û Þ Û Û Û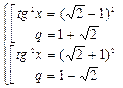

 

Рекомендации по проверке. Все значения q найдены, но не исключено q =1 – 6 баллов.

 

3. Решить уравнение в целых числах x ⁴ – 2 y ⁴ – 4 z ⁴ – 8 t ⁴ = 0.

Ответ: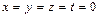

Решение. Заметим, что x –четное. Пусть x =2 x ₁, тогда получаем, что

, но тогда y –четное. Пусть y =2 y ₁, тогда . Следовательно, z =2 z ₁ и . Аналогично t =2 t ₁ и получаем исходное уравнение, но для переменных x ₁, y ₁, z ₁, t ₁, следовательно, для них мы можем проделать те же самые рассуждения и т.д. Получаем, что каждая переменная делится на произвольную степень 2. Следовательно, x = y = z = t =0.

Рекомендации по проверке.

1) Замечено, что x –четное – 1 балл.

2) С помощью верных рассуждений получено уравнение где x =2 x ₁, y =2 y ₁, z =2 z ₁, t =2 t ₁, но нет соответствующего вывода – 4 балла.

3) Приведен только ответ без доказательства, что других решений нет – 0 баллов.

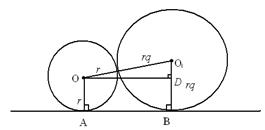
4. На столе лежат три мяча, попарно касаясь друг друга. Радиусы мячей образуют геометрическую прогрессию со знаменателем q ≠1. Радиус среднего из них равен 2012. Найдите отношение суммы квадратов сторон треугольника, образованного точками касания мячей стола, к сумме сторон треугольника образованного центрами мячей.

Ответ: 4024

Решение. Пусть радиус меньшего из мячей равен r, тогда радиусы остальных rq =2012 и rq ², а точки касания мячей стола обозначим A, B, C соответственно. Рассмотрим сечение двух мячей плоскостью перпендикулярной плоскости стола и проходящей через центры данных мячей (см. рисунок, для двух меньших по величине мячей). Тогда для шаров приведенных на рисунке получаем, что ОA = r, O₁B = rq и OO ₁= r + rq. Далее, O ₁ D = O ₁ D–DC = O ₁ B–OA = r (q– 1). Из ∆ OO ₁ D по теореме Пифагора получаем, что OD = = AB. Аналогично, рассматривая оставшиеся пары мячей, получим, что AC = 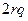, BC = , тогда искомая величина равна

Рекомендации по проверке. За вычисление всех сторон треугольника, образованного точками касания мячей – 2 балла.

5. Школьник Петя на карточках выписывал три натуральных числа, каждое из которых от 1 до 20. Причем нет двух карточек с одним и тем же набором чисел. Докажите, что найдутся две карточки, имеющие ровно одно общее число, если известно, что Петя заполнил 21 карточку.

Решение. Докажем от противного. Тогда не существуют двух карточек, имеющих ровно одно общее число. Назовем карточки «похожими», если они имеют два общих числа.

Лемма: Если карточки A, B «похожие» и карточки B, C «похожие», тогда карточки A и C тоже «похожие».

Доказательство. Пусть карточка A состоит из чисел a, b, с, а карточка B состоит из чисел a, b, d. Тогда число a или b должно входит в карточку С, так как карточки B и C «похожие». Но так у карточек A и C не может быть одного общего числа, значит их два, т.е карточки A и C «похожие».

Из леммы следует, что все карточки можно разбить на группы так, что в одну группу попадают только «похожие» карточки. Тогда возможны следующие три ситуации:

1) Группа содержит только карточки, на которых написаны только три различных числа, но тогда данная группа содержит только одну карточку с данными числами.

2) Группа содержит только карточки, на которых написано четыре различных числа. Но тогда карточек в группе не более 4.

3) Группа содержит более четырех различных чисел.

Пусть карточка A состоит из чисел a, b, с, а карточка B состоит из чисел a, b, d. Пусть существует число e, отличное от чисел a, b, c, d написанное на какой-либо карточке C из этой группы. А так как все карточки в группе «похожие», то карточка С должна содержать числа a, b. Таким образом, все карточки данной группы должны содержать числа a, b. Значит число карточек в данной группе ровно на два меньше чем число чисел используемых в данных карточках.

Таким образом получаем, что всего карточек не больше количества используемых чисел. Получили противоречие.

Составитель всех задач 11 класса К.В. Трунов.

Задача 4 составлена совместно с В.И. Луценко

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: