Научные теории и методы их построения

 

Так как теория в данном параграфе становится предметом специального рассмотрения, то согласно методологическим требованиям введения понятия мы должны ее явно определить. Оказывается, что сделать это не так-то просто. Причем немаловажной помехой в решении этой задачи является наше интуитивное представление о теории. Обычный школьный или вузовский опыт подталкивает нас к тому, чтобы характерные черты изучаемых в школе или вузе теорий принять за специфические признаки теории вообще, чего как раз и нельзя делать в условиях современной науки.

Поэтому подвести читателя к существенным общим и специфическим признакам теории целесообразно не со стороны интуитивного представления о теории, а со стороны рассмотрения языковых систем и выделения в них теорий как специфических языковых образований.

Начнем с того, что общеизвестные теории действительно являются языковыми образованиями в разговорном языке, зачастую специфицированном. Но мы уже знаем, что кроме этого языка имеется много языков других типов и видов. Поэтому напрашивается общий вывод о том, что теорией может быть некоторого рода языковая система в любом языке, а не только в естественном. Но мы уже знаем, что языки могут быть языками различных семиотических типов. Поэтому и теории могут быть теориями различных семиотических типов.

В частности, мы уже знакомы с чисто формальными языками. Значит возможны формальные теории как некоторые образования в этом языке. Но, как мы знаем, чисто формальные языки не имеют семантики и непосредственно не могут служить для отображения действительности. Значит опять-таки придется смириться с мыслью о том, что могут существовать теории, непосредственно не отображающие действительности, однако непременно имеющие возможность, хотя бы в потенции, отображать ее.

Для определения общего понятия о теории, пригодного для теорий во всех языках, необходимо гносеологическому признаку теории "иметь возможность отображать действительность" поставить в соответствие семиотический признак, так как не все теории должны быть непосредственно гносеологическими. Каким должен быть этот семиотический признак?

Для того, чтобы его сформулировать, вспомним, что язык является множеством терминов и предложений. Выделим в языке множество предложений. Любым ли множеством предложений языка может быть теория? Нет, не любым, ибо теория не должна содержать логического противоречия. Иначе она не сможет хотя бы потенциально быть отображением действительности. Поэтому теория не может совпадать с множеством предложений языка. Иначе в теории, как и в языке, будут иметься как некоторое предложение, так и его отрицание, а тем самым и истинное, и ложное предложения. В языке это допустимо, а в теории - нет.

Наличие совместно истинного и ложного предложений (А и не-А) делает теорию вообще непригодной для отображения действительности. Почему? Да потому, что в материальной действительности не может существовать объект, обладающий и не обладающий одним и тем же свойством одновременно. Об этом свидетельствует весь опыт человечества и все научное познание. Недаром науками иногда прилагаются огромные усилия, чтобы освободить теорию от противоречия, если оно там все же встречается.

Отсюда следует, что специфическому гносеологическому признаку теории быть, по меньшей мере, в возможности применимой для отображения действительности необходимо сопоставить специфический семиотический признак теории быть множеством предложений, не совпадающим со всем множеством предложений языка, т.е. быть логически (синтаксически и семантически) непротиворечивым подмножеством предложений языка. К тому же теория не может не иметь вообще никаких предложений, т.е. она должна быть непустым множеством предложений. Имея определяющий семиотический признак теории, можно дать общее семиотическое понимание теории, независимое от отношения теории к действительности и опирающееся только на язык, его системы и его свойства. Такое определение следующее: теория есть дедуктивно организованное множество общих предложений языка. Но есть и более формальные определения: теория в некотором языке есть (1) непротиворечивое и непустое подмножество предложений этого языка, или (2) правильное (не совпадающее со всем множеством) подмножество предложений языка[50].

Второе определение теории более общее, чем первое, так как из второго первое просто следует, а из первого второе – нет. В самом деле, предположим, что мы имеем правильное подмножество предложений языка, но противоречивое. Из противоречия следует "все, что угодно", в том числе и то, что наше правильное подмножество совпадает со всем множеством предложений языка, т.е. не является правильным. Полученное противоречие доказывает, что из второго определения следует первое. Но обратное неверно, так как есть языки, не содержащие в алфавите отрицания. В них нельзя сформулировать противоречия "А и не-А". Поэтому второе определение теории в этих языках имеет место, а первое – нет.

Из общего определения теории следует и общий

Метод построения теорий в любом из языков:

Необходимо построить некоторый язык или принять какой-то из существующих языков.

Выбрать подмножество предложений данного языка.

Обосновать, что оно является правильным (или непротиворечивым) подмножеством языка.

Казалось бы, с построением теорий дело обстоит очень просто. Однако общее определение теорий дает только необходимый признак всякого рода теорий. Но он не является достаточным для любого рода теории. Признак правильности подмножества является необходимым и достаточным только для чисто формальных теорий. Руководствуясь этим признаком, можно строить сколько угодно формальных теорий, что на самом деле и делается. Например, в формальной логике построено огромное количество так называемых многозначных логик и модальных логик.

Для содержательных теорий признак правильности подмножества (или непротиворечивости) уже не достаточен, хотя и необходим. Стало быть, нужно более узкое определение термина "содержательная теория". Для гносеологической содержательной теории определение должно быть еще более узким. А для конкретных гносеологических теорий совсем узким, зависящим от специфики идеализаций, принимаемых данной теорией.

Содержательная теория – это семантически непротиворечивое (не содержащее истинные предложения и ложные совместно) подмножество множества предложений содержательного языка.

Более общим определением содержательной теории будет ее определение через признак быть правильным подмножеством истинностных значений в множестве всех истинностных значений языка. Пусть, например, предложения языка имеют два значения – истина и ложь. Тогда теорией может быть подмножество предложений, имеющих значение истины. Но не истины и лжи совместно. Это общеизвестно и никаких возражений не вызывает.

Однако согласно определению теорией может быть и подмножество предложений, имеющих оценку "ложно", но уже без истинных предложений. В обычных науках такого не бывает. Но такие теории, состоящие только из ложных предложений, действительно строятся и даже имеют немаловажное значение в решении определенных задач. Например, Я. Лукашевич такие теории использовал для решения метатеоретических проблем. Если язык имеет предложения с тремя истинностными оценками, то могут быть теории с одной и двумя оценками своих предложений, и т.д. Это дает метод построения любых содержательных теорий в содержательном языке (не обязательно гносеологических, к которым мы привыкли в школе или в вузе):

Уточнить истинностные оценки предложений содержательного языка.

Выделить во множестве этих оценок правильное подмножество истинностных оценок (они называются выделенными значениями).

С помощью определенного метода построения теории, о котором речь пойдет ниже, задать множество предложений языка, имеющих только выделенные значения.

Что касается конкретных теорий, то для их определения нужны многие спецификации. Вообще это весьма трудный вопрос, потому что выделение конкретной теории из всех теорий некоторого класса дело весьма непростое. Главное же состоит в том, что не всякая построенная конкретная теория принимается в число научных теорий. Например, соблюдая все методологические правила построения теорий в содержательном языке ньютоновой механики наряду с механикой самого Ньютона можно построить огромное количество иных теорий. Но пока нет данных, чтобы какая-то из них была принята научным сообществом.

Здесь возникает проблема критерия принятия теории в любом из языков: хоть в формальном, а хоть и в содержательном. Это критерий не семиотического и не методологического, а прагматического характера. Это критерий практики. Он состоит в применимости теории для решения научно-практических задач. При этом даже не обязательна интерпретация теории на какой-либо области объективной действительности. Известно, что сходят со сцены теории, имеющие интерпретацию в материальной действительности, например, аристотелева механика, основанная на эмпирически данном факте движения тел только под воздействием сил. Однако эта механика уступила место механике Галилея-Ньютона, основанной на предпосылке о естественном состоянии движения без воздействия сил, которая не имеет эмпирической интерпретации. Несмотря на это механика Галилея-Ньютона имеет неоспоримые преимущества в решении научно-практических задач перед механикой Аристотеля.

По мнению М. Клайна[51]небесные механики Птолемея, Коперника и Кеплера не превосходят друг друга в эмпирической интерпретации. Но теория Кеплера дает более простой и более точный метод решения практических астрономических задач и по этой причине вытеснила теории Птолемея и Коперника. Что касается квантовой механики, то ее понятия не имеют аналогов в эмпирической действительности, хотя теория способна решать научно-практические задачи огромной важности. Подобных примеров достаточно много. Все они говорят в пользу того, что основной критерий принятия теории является критерий практики, т.е. способность теории решать научно-практические задачи. Последнее является, как мы говорили в главе III, и критерием истинности теории как ее способности адекватно отображать объективную действительность.

В соответствии с семиотической типологией языков построение теорий в этих языках приводит к следующей семиотической типологии теорий:

 

 

 

Дадим к этой схеме некоторые пояснения. Что такое общее понятие теории, уже было разъяснено. Поясним суть теорий частных типов и видов. Теория в специфицированном языке есть теория со специфицированной терминологией (или правильное подмножество предложений специфицированного языка). К таким теориям относятся почти все теории естественных и гуманитарных наук, так что примеры общеизвестны.

Формальная теория - это теория, предложения которой распознаются только по форме слов языка с помощью формальных правил (алгоритмов), являющаяся правильным подмножеством формального языка. Чисто формальная теория - это формальная теория, не имеющая интерпретации или рассматриваемая независимо от интерпретации (с точностью до интерпретации). Формально-содержательная теория - теория формальная, имеющая интерпретацию. Теория гносеологическая (содержательная или формально содержательная) - теория, интерпретированная в области систем объективной действительности (правильное подмножество предложений гносеологического языка). Негносеологическая содержательная теория - это теория, интерпретированная на системе абстрактных объектов.

Здесь представлен семиотический подход к классификации и определению теории, так как именно этот подход особо важен для методологии теоретического познания. Но он при необходимости дополняется другими подходами, например, гносеологическим, прагматическим и т.п. На базе семиотического подхода можно сформулировать общие методы построения теорий:

1. Метод разрешающей процедуры.

В общем виде он состоит в формулировке правил, согласно которым из всех слов языка теории выбираются предложения, принадлежащие теории, и отбрасываются предложения, которые ей принадлежать не должны. Для большинства естественных и гуманитарных теорий таким правилом является отбор истинных предложений определенной специфики, определяемой предметом теории, ее идеализациями, ее практическим применением и т.п. факторами. Так как эти факторы не слишком определены, то твердо решить вопрос, принадлежит ли данное предложение языка некоторой теории или не принадлежит, достаточно трудно.

Для некоторых формальных теорий разрешающая процедура представляет алгоритмическое правило. Это правило чисто механически позволяет решать вопрос о принадлежности предложения языка теории определенной теории в этом языке. Например, имеется алгоритм, по которому относительно любого предложения языка классической логики высказываний, можно сказать, принадлежит оно логике высказываний или не принадлежит. Однако такие разрешающие алгоритмы невозможны для неформальных (чисто содержательных) теорий и далеко не всегда возможны даже для формальных теорий. Поэтому более употребим ниже описываемый метод построения теории.

2. Метод перечисляющей процедуры.

Он предполагает наличие правила, позволяющего распознать среди предложений языка теории предложения ей принадлежащие. Но он не может распознать предложения, не принадлежащие теории. Образно говоря, он перед ними становится в тупик и ничего не может сказать: ни да, ни нет.

К такому методу относится дедуктивно-аксиоматический метод, который состоит в следующем:

В языке теории выбираются некоторые предложения, которые сразу же объявляются на каких-то основаниях принадлежащими данной теории. Эти предложения получили название исходных предложений теории. В некоторых науках они называются аксиомами, в других – исходными принципами, постулатами.

Выбирается логика, с помощью которой из исходных предложений теории получаются производные предложения. Обычно применяется в естественных и гуманитарных науках классическая логика. Но выше мы уже говорили о том, что могут быть случаи, когда проблема выбора логики, согласующейся с истинностными значениями предложений теории, является существенной и не тривиальной.

Путем вывода из исходных предложений производных строится вся теория. Тут правила дедуктивного вывода как бы перечисляют предложения теории. Поэтому и метод построения называется перечисляющей процедурой.

Для формальных теорий аксиоматический метод построения теорий является формально-аксиоматическим. В этом случае формальная логика позволяет действительно получать неограниченную последовательность предложений теории. Однако получение производных предложений теории из ее исходных предложений только по правилам формальной логики возможно в достаточной мере лишь для логики и математики и некоторых фрагментов других наук.

Утверждать, что так обстоит дело в естественных, а тем более в гуманитарных науках, было бы преждевременным. Это скорее цель, а не реальность. Относительно этих наук можно сказать лишь то, что исходные принципы, если они вообще могут быть достаточно определенно выбраны, как-то предопределяют другие предложения теории, хотя последние логически и не следуют из первых. Они играют роль ограничивающих условий для формулировки предложений теории. Как правило, в естественных и гуманитарных науках чисто дедуктивным путем можно построить лишь отдельные их фрагменты. Вообще, аксиоматика – это высший этап дедуктивной организации теории.

В случае же построения теории или ее фрагментов в виде дедуктивных систем, эти системы будут являться логическими системами, т.е. системами, все термины и предложения которых логически обусловлены исходными терминами и предложениями. Логическое обусловливание осуществляется с помощью правил логики, называемых уже логикой теории, т.е. системой правил, по которым из исходных предложений теории выводятся ее производные предложения с сохранением определенной их семантической оценки (логически истинно, фактуально истинно, конструктивно истинно т.п.). Логика теории относительна, ее выбор зависит от природы (специфики) семантического значения предложений теории, которое логические правила должны сохранять.

Рассмотрев условия построения теорий, можно охарактеризовать частные методы построения теорий нижеприведенных семиотических типов. Эти методы следуют из определений теорий. Так, метод построения формальных теорий состоит в следующем:

Строится формальный язык.

В этом языке задаются правила принятия предложений теории (методом разрешения или перечисления).

Если стоит задача построения не просто чисто формальной, а формально-содержательной теории, то задаются семантические правила интерпретации. В зависимости от специфики объектов области интерпретации она может быть гносеологической или негносеологической.

Метод построения специфицированных теорий следует из их определения: строится специфицированный язык, а затем каким-либо из методов принятия предложений теории строится сама теория. Например, методология строится так:

1. Берется естественный разговорный язык.

2.Вводятся специфицированные термины, перечисленные в терминологическом указателе данной работы. На этой основе создается специфицированный язык методологии.

3. В данном языке формируются принципы и методы, например, те, которые перечислены в содержании данной работы. Принципы должны быть истинны применительно к идеализациям, принимаемым методологией. Методы должны быть адекватными решению поставленных перед методологией задач по введению понятий, постановке вопросов, обоснованию суждений, построению теории и т.п.

Как видно из формулировки метода построения специфицированных теорий, существенную роль в применении этого метода играет введение основных понятий и формулировка принципов, которые должны отвечать определенным методологическим требованиям. Так, метод введения основных понятий должен удовлетворять следующим требованиям:

 

1.Требование эффективности. Это требование диктуется тем, что определение понятия должно позволять достаточно четко распознавать определяемый объект. Иначе будет неясно, что и о чем утверждается, но в таком случае достаточно определенно установить истинность утверждений, в том числе и принципов, будет невозможно. Построенная на неэффективных понятиях теория будет очень неточной (неопределенной). Чтобы принципы были эффективными, необходимы эффективные понятия для их формулировки.

 

2.Требование применимости. Требование состоит в том, чтобы понятия, с помощью которых формулируются принципы и методы теории, были определены применительно к основным задачам, решаемым теорией. Именно последнее условие является решающим для введения понятия.

 

3. Предполагается выполнение требований к введению понятий,

изложенных в главе 1.

Метод формулировки принципов теории:

Дать название принципу.

Название – это словосочетание. Оно может указать на ученого, сформулировавшего принцип, на отношение, которое принцип выражает и т.п. Вообще говоря, о названиях не спорят. Название ничего не утверждает и поэтому не истинно и не ложно, а принцип есть истинное утверждение. Поэтому название принципа нельзя принимать за сам принцип, что, к сожалению, иногда наблюдается.

Например, принцип, нечто утверждающий о соотношении силы тока, напряжения и сопротивления, называют законом Ома, т.е. по фамилии сформулировавшего этот принцип ученого. Данный принцип можно было бы назвать принципом соотношения силы тока, напряжения и сопротивления. При этом в названии ничего не утверждается о природе этого соотношения, хотя содержится некоторая информация о нем.

2.Определить основные понятия, входящие в формулировку принципа.

Напомним, что основными понятиями являются понятия о том, что утверждается и о чем утверждается в формулировке принципа и, как правило, они определяются до его формулировки, либо непосредственно за ней.

3. Сформулировать принцип, т.е. изложить, что и о чем он утверждает.

Например, принцип (закон) Ома формулируется так: напряжение равно произведению силы тока на сопротивление. Основными понятиями тут являются понятия о силе тока, напряжении, сопротивлении и о произведении соответствующих физических величин. Все эти понятия необходимо определить до утверждения о соотношении этих величин. Иначе мы не получим самого утверждения (принципа).

4. Обосновать истинность принципа.

Обоснование может проводиться непосредственным или опосредованным методами. Опосредованное обоснование исходного принципа данной теории не может производиться с помощью других принципов этой же теории. В обосновании могут применяться методы разрешающей и перечисляющей процедур. Методы обоснования зависят от типа теории. Для обоснования формальных теорий существенное значение имеют методы метатеории. Специфику обоснования содержательных гносеологических теорий поясним ниже.

5. Показать применимость принципа для решения научно-практических задач

Мы достаточно хорошо показали применимость принципов относительности и плюрализма истинности.

Поясним применение вышеизложенных требований на примере построения такой специфицированной теории, какой будет являться ниже описываемый фрагмент теории познания. Логика построения сообщает о том, что надо выбрать основные понятия, сформулировать принципы и показать их истинность и практическое применение для решения научно-практических задач. Однако история создания теорий свидетельствует о том, что этот порядок вообще строго не обусловлен, что он характеризует лишь последний этап построения теории. На самом деле в начале построения теории исходят из определенных задач.

При построении фрагмента теории познания мы тоже будем вводить основные понятия и принципы, ориентируясь на решение проблем, изложенных в § 4 главы III. Исходя из целей практического применения фрагмента теории познания, мы подбираем необходимые для этого решения принципы, а тогда, естественно, для формулировки принципов вводим и соответствующие понятия. Но эта работа остается «за кадром». Реципиенту же важна лишь логика этого процесса.

Специфицированные теории составляют основную часть научного познания, как естественного, так и гуманитарного. Однако и формальные теории, особенно распространенные в логике и математике, тоже имеют немаловажное научное значение.

На основе построенных теорий можно строить новые теории. Будут они приняты научным сообществом или нет, – это уже другой вопрос, решаемый с прагматических позиций. Для методологии важно лишь то, чтобы они были правильно построены. Для этого имеются специальные методы, например, следующие:

(А) Метод пролиферации, состоящий в следующем:

Выбирается только фактуально истинная теория,которую будем далее именовать исходной теорией. Логически истинная теория для целей построения методом пролиферации не может быть использована по причинам, которые были изложены в главе III (вспомним, что если А логически истинно, то не-А не может быть истинным ни в какой теории). Допустим, мы выбрали содержательную (фактуально истинную) евклидову геометрию, так как на примере этой теории применение метода пролиферации представляет весьма простой случай.

Выявляются исходные принципы теории. Для евклидовой геометрии такими принципами являются 18 аксиом[52]. Последней в этом списке является аксиома о параллельных Евклида, которую обозначим через А18, а остальные аксиомы обозначим через А1, …, А17. Так как дальнейшие операции не зависят от содержания теории (от её интерпретации) и так как старое содержание все равно надо будет заменять новым на последнем этапе построения новой теории, то от содержания исходной теории следует отвлечься. Тогда теория будет выступать как чисто формальная теория, ее предложения будут рассматриваться просто как строчки символов (как формальные предложения). В нашем случае аксиомы А1 – А18 станут формальными аксиомами, не имеющими содержания. Но, повторяем, на содержание нам опираться уже будет не нужно.

Выбирается принцип, который логически не зависит от других исходных принципов теории. Это значит, что ни выбранный принцип не должен быть выводим из остальных принципов и ни его отрицание. В нашем случае выберем аксиому А18. В геометрии уже доказано, что ни А18, ни отрицание А18, из А1, …, А17 не выводимы.

Выбранный принцип из исходной теории удаляется и заменяется на его отрицание. В нашем примере из списка аксиом А1, …, А18 удаляется А18 и заменяется на отрицание А18, т.е. на не-А18, которая является аксиомой о параллельных Лобачевского.

Полученной в результате замены в системе формальных предложений интерпретации подыскивается новая интерпретация, так как старая интерпретация заведомо невозможна. Это потому, что при одной и той же интерпретации не могут быть истинны как некоторое предложение, так и его отрицание. Полученная система принципов должна быть так же фактуально истинной.

В нашем случае аксиомы А1 – А18 были истинны при интерпретации на евклидовом пространстве. От этой интерпретации мы отказались и построили систему аксиом А1-не-А18. Теперь этой системе надо придать новую интерпретацию. Такая интерпретация известна. Это пространство Лобачевского. На нем все аксиомы А1-не-А18 фактуально истинны.

В результате получается из исходной теории новая теория. У нас получилась теория А1, …, А17, не-А18, представляющая геометрию Лобачевского. Так как исходная геометрия Евклида была фактуально истинна, то геометрия Лобачевского, не совместимая с геометрией Евклида, тоже может быть только фактуально истинной. Что на самом деле и имеет место при упомянутой интерпретации.

Методом пролиферации можно построить многие теории в математике (не канторовская теория множеств, не архимедов математический анализ и т.п.) и физике (релятивистская механика, квантовая механика и др.).

(Б) Метод эффективизации понятий, суть которого можно изложить так:

Берется исходная теория, содержащая неэффективные понятия (а тем самым и принципы).

Например, возьмем ньютонову механику, которая содержит неэффективное понятие одновременности. Оно не эффективно потому, что не предполагает какой-либо физически осуществимый метод установления того факта, одновременны события А и В или нет. Решение этого вопроса предоставляется нашей интуиции.

Производится эффективизация некоторых понятий исходной теории. Зависимая от специфики понятий той или иной науки эффективизация может проводиться различными методами. В математике эффективизация проводится методом алгоритмических определений. Например, интуитивное понятие об алгоритме эффективизируется с помощью его алгоритмического определения и получается эффективное понятие алгоритма (рекурсивная функция и т.п.).

В физике алгоритмизация практически не применяется. Зато используется метод квантификации, когда качественные понятия превращаются в количественные, т.е. когда они становятся понятиями о величинах. Это дает возможность формулировать законы на математическом языке и делать вычисления.

В гуманитарных науках ни тот, ни другой методы эффективизации понятий практически не применимы. Поэтому эффективизация происходит за счет системного подхода, уточнения идеализаций и т.п. Примеры такой эффективизации были приведены в главе I.

В нашем примере надо эффективизировать понятие одновременности. Такую эффективизацию провел А. Эйнштейн[53], связав понятие одновременности с физически осуществимым явлением - распространением луча света. Чтобы определить, одновременны события А и В или нет, надо выбрать лежащую между ними среднюю точку С. Возникновение событий должно сопровождаться посылкой в точку С лучей света. Если лучи света встретятся в точке С, то события одновременны. Если они встретятся правее или левее точки С, то не одновременны. И это обстоятельство эффективно установимо. В отличие от неэффективного понятия одновременности, неявно предполагавшегося Ньютоном, эйнштейновское понятие одновременности можно назвать эффективной одновременностью.

3. На основе эффективизированных понятий производится перестройка исходной теории: переформулировка одних понятий и принципов, удаление других, введение третьих. В итоге получается новая теория, более эффективная, чем исходная.

В рассматриваемом нами примере оказывается, что эффективизация одновременности ведет к эффективизации понятий отрезков пространства и времени, а также понятий массы, скорости, силы и т.п. а это, в свою очередь, ведет к замене принципов абсолютности (неизменности во всех инерциальных системах отсчета) пространственных и временных отрезков, массы, силы, скорости и т.п. на принципы относительности, различия в разных системах отсчета) этих величин. Последнее приводит к удалению принципов преобразований Галилея и замене их принципами преобразования Лоренца. В итоге получается из ньютоновой механики новая релятивистская механика.

Мы уже говорили в главе I о том, что можно эффективизировать такие понятия философии как категории сущности, необходимости, формы, отражения, истинности и т.п. На этой основе можно сформулировать более эффективные философские принципы, например, более эффективный принцип относительности истинности. Можно сформулировать и другие эффективные принципы. В итоге получим новый вариант философской теории.

(В) Метод обобщения.

Суть его в следующем:

1. Исходной теорией является теория, законы которой могут быть записаны на логико-математическом (или ином точно построенном) языке. Эти законы рассматриваются с точностью до математической семантики, т.е. в отвлечении от специфической частно-научной семантики. Например, возьмем закон ньютоновой механики 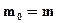, который сообщает о том, что масса тела в инерциальной системе отсчета (в которой тело движется) равна его массе в собственной системе отсчета (в которой тело покоится) . 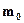Рассмотрим этот закон с точностью до математической семантики. Тем самым отвлечемся от того, что это физические величины - массы. Тогда они предстанут просто как математические величины - переменные для действительных чисел. И закон превратится в математическое уравнение 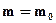, где и 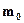- переменные для чисел, и только.

2. Полученные математические уравнения обобщаются с помощью математических тождественных преобразований и метода обобщениялогики. Так, формулу 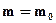можно с помощью тождественных преобразований и обобщения привести к виду

. Это делается так: . Затем число 0 заменяется по правилу обобщения на переменную , частным случаем которой оно является, и получается формула .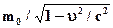

3. Получившимся в результате обобщения уравнениям придается новая интерпретация, в результате чего строится новая теория. В нашем случае уравнению 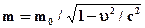придается релятивистская интерпретация символам массы, скорости и постоянной скорости света 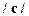. В итоге получим закон релятивистской механики из исходного закона ньютоновой механики.

По методам пролиферации, эффективизации и обобщения (а также и другим, которые здесь не были упомянуты) практически каждый может строить новые геометрии, физики и другие теории. Но будут ли они приняты? Этот вопрос можно решить лишь демонстрацией того, что созданная теория может решать такие научно-практические задачи, которые не решала прежняя теория или решала их хуже. Прагматический критерий в решении этой проблемы является определяющим. Поэтому рассмотренные методы построения новых теорий весьма полезны в качестве эвристических методов. Строя с их помощью теории и проверяя их на практическую применимость, можно построить теорию, которая будет принята в число научных теорий.

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: