 |
Элементарные преобразования матрицы
|
|
|
|
Таблица подготовки к экзамену
| (1) повторить | 1. Ранг матрицы. Вычисление ранга матрицы. Теорема о базисном миноре. |
| (2) повторить | 2. Элементарные преобразования матрицы. Теорема о ранге матрицы. |
| (2) | 3. Системы линейных алгебраических уравнений. Основные понятия. Матричная запись системы. |
| (2) | 4. Критерий совместности системы. Теорема Кронекера-Капелли. |
| (3) | 5. Теорема Крамера. |
| Не давалось. Только если успею | 6. Метод Гаусса решения систем линейных алгебраических уравнений. |
| (3) | 7. Однородные системы линейных алгебраических уравнений. свойства решений. Линейная зависимость и линейная независимость решений. Критерий существования ненулевых решений. |
| (3) повторить определение ФСР | 8. Фундаментальная система решений однородной системы линейных алгебраических уравнений. Структура общего решения системы. |
| (3) | 9. Неоднородная система линейных алгебраических уравнений. Свойства её решений. Структура общего решения системы. |
| (3) аксиомы и свойства | 10. Линейные пространства. Определение. Свойства. Примеры линейных пространств. |
| (3) | 11. Базис и размерность линейного пространства. Теорема о связи базиса и размерности линейного пространства. |
| (3) | 12. Матрица перехода от одного базиса к другому. Преобразование координат при переходе к новому базису. |
| (3) | 13. Подпространства линейного пространства. Линейная оболочка. Теорема о размерности линейной оболочки. |
| (4) | 14. Пересечение и сумма подпространств линейного пространства. Прямая сумма подпространств. Разложение пространства в прямую сумму подпространств. |
| (4)!!!!!! Теорема о размерности из 17! | 15. Линейные операторы. Определение. Свойства. |
| 16. Матрица линейного оператора. Единственность матрицы линейного оператора. Преобразование матрицы при переходе к другому базису. | |
| 17. Образ и ядро линейного оператора. Теорема о размерности образа и ядра линейного оператора. | |
| См вопр 15 | 18. Обратный оператор. Критерий его существования. |
| (5) повторить | 19. Собственные значения и собственные векторы линейного оператора. Характеристическое уравнение. Нахождение собственных векторов. |
| (6) | 20. Билинейные формы. Матрица билинейной формы. Её преобразование при переходе к новому базису. |
| (7) | 21. Квадратичная форма. Приведение к каноническому виду методом Лагранжа. |
| (7) | 22. Закон инерции квадратичных форм. Критерий Сильвестра положительной определённости квадратичной формы. |
| 23. Евклидово пространство. Скалярное произведение. Его свойства. | |
| 24. Ортонормированный базис. Ортогонализация по Шмидту. | |
| 25. Приведение квадратичной формы к каноническому виду ортогональным преобразованием. | |
Ранг матрицы. Вычисление ранга матрицы. Теорема о базисном миноре.
|
|
|
Теорема о линейной зависимости строк, Минор к-го порядка, ранг матрицы, базисный минор, базисные строки и столбцы, теорема о базисном миноре
НЕОБЯЗАТЕЛЬНОЕ
КОНЕЦ НЕОБЯЗАТЕЛЬНОГО
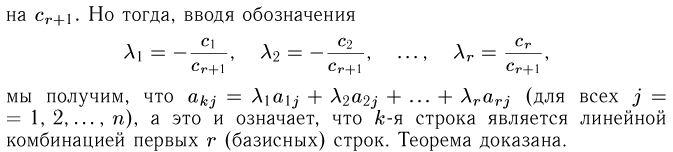ДАЛЕЕ НЕОБЯЗАТЕЛЬНОЕ
КОНЕЦ НЕОБЯЗАТЕЛЬНОГО
Элементарные преобразования матрицы. Теорема о ранге матрицы.
Элементарные преобразования матрицы
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
|
|
|
Элементарными преобразованиями над строками матриц называются следующие преобразования строк:
1. умножение строки на ненулевое число; (умножая уравнение на число, корни не меняются)
2. перестановка двух строк; (если в системе два уравнения поменять местами, корни не меняются)
3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число. (если делать это с уравнениями, корни не меняются)
НЕОБЯЗАТЕЛЬНОЕ
Доказательство свойства 3
КОНЕЦ ОБЯЗАТЕЛЬНОГО
Если от матрицы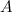 
к матрице 
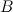перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают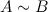 
|
|
|
