 |
Сумма и пересечение подпространств
|
|
|
|
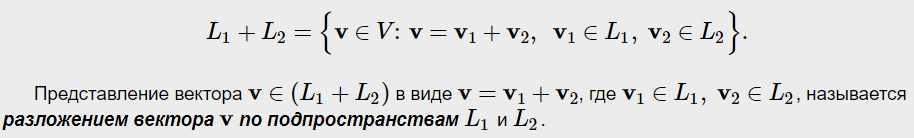
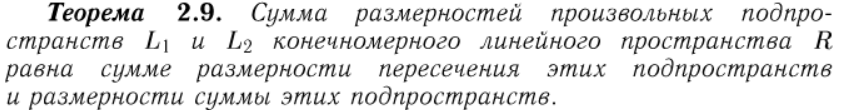
Утверждение из пункта 1:
Конец утверждения
Отступление. Почему подпространству суммы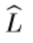 
принадлежат все эти элементы 2.14?
Обозначения на картинке ниже отличаются от тех, что в доказательстве, но смысл понятен: любой вектор подпространства суммы v=v1+v2, где v1 – принадлежит L1, а v2 – принадлежит L2. В свою очередь v1 разложим по базису подпространства L1, т.е.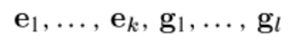 
, а v2 по базису подпространства L2, т.е. 
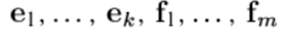, следовательно любой вектор v подпространства суммы 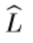будет раскладываться по этому общему базису подпространств L1 и L2. Т.е. 
http://mathhelpplanet.com/static.php?p=peresechenie-i-summa-podprostranstv
Конец отступления.
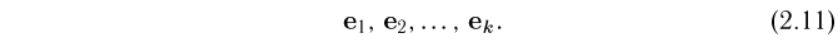
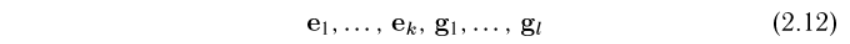
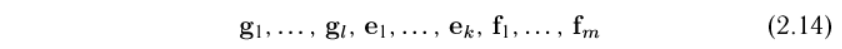
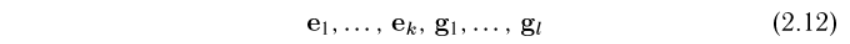
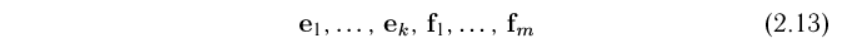
Если непонятно, смотри тут http://mathhelpplanet.com/static.php?p=peresechenie-i-summa-podprostranstv
Разложение линейного пространства в прямую сумму подпространств
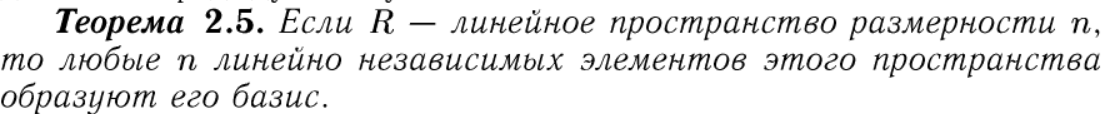
Линейные операторы. Определение. Свойства.
Определение линейного оператора
Действия над линейными операторами. Пространство линейных операторов.
Свойства множества L(V, V) линейных операторов
Тождественный (единичный) оператор, произведение операторов, обратный оператор, теорема о прообразе нулевого вектора, взаимно однозначное отображение, теорема о взаимно однозначном отображении, теорема об обратном операторе
Из того, что оператор действует взаимно однозначно следует, что у него имеется обратный оператор.
То же самое, но с пояснением
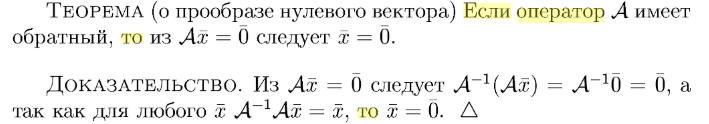
Конец пояснения
Далее теорема приведена из другого учебника, т.к. в Ильине доказательство неполное и не так доступно.
Вопрос 17
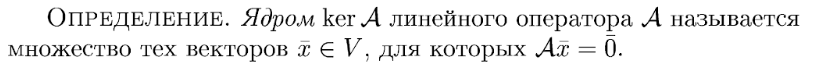
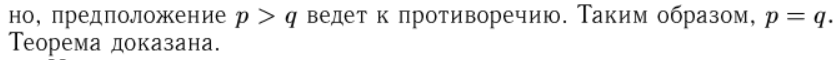
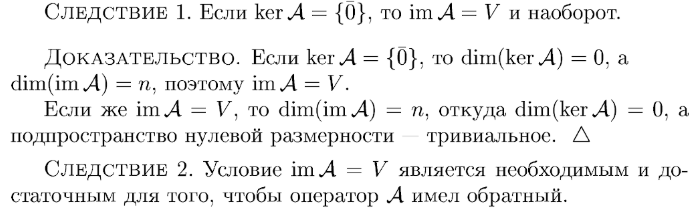
Матрица линейного оператора. Единственность матрицы линейного оператора. Преобразование матрицы при переходе к другому базису.
|
|
|
Матрицы линейных операторов в заданном базисе линейного пространства
Преобразование матрицы линейного оператора при переходе к новому базису
Альтернатива
Характеристический многочлен линейного оператора
Образ и ядро линейного оператора. Теорема о размерности образа и ядра линейного оператора.
См вопрос 15
Обратный оператор. Критерий его существования.
Более последовательно См вопрос 15
Критерий 2
Аналогичный критерий 3
Собственные значения и собственные векторы линейного оператора. Характеристическое уравнение. Нахождение собственных векторов.
Билинейные формы. Матрица билинейной формы. Её преобразование при переходе к новому базису.
Понятие билинейной формы
Более простым примером можно назвать скалярное произведение векторов. Оно также является числовой функцией от двух векторных аргументов.
Представление билинейной формы в конечномерном линейном пространстве.
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы.
Квадратичная форма. Приведение к каноническому виду методом Лагранжа.
Понятие квадратичной формы
(вид 7.3 и теорема
)
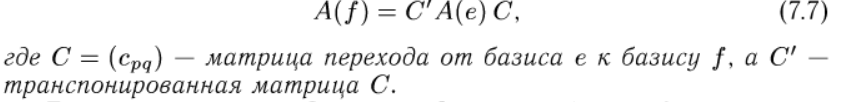
Метод Лагранжа
Закон инерции квадратичных форм. Критерий Сильвестра положительной определённости квадратичной формы.
Закон инерции квадратичных форм
НЕ ДАВАЛСЯ ЭТОТ ПУНКТ
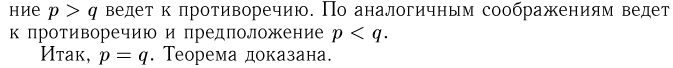
КОНЕЦ ТОГО, ЧТО НЕ ДАВАЛОСЬ
Критерий Сильвестра положительной определенности квадратичной формы.
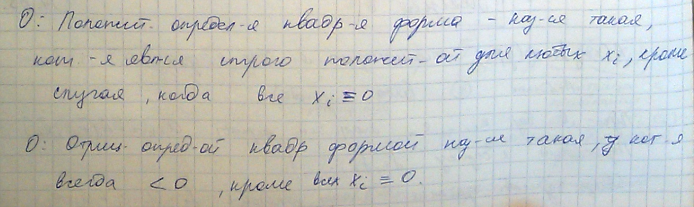
Если же хотя бы один минор противоположного знака (при этом не равен нулю!), то форма знакопеременна.
Евклидово пространство. Скалярное произведение. Его свойства.
Определение вещественного евклидова пространства
|
|
|
Простейшие свойства произвольного евклидова пространства
Неравенство Коши-Буняковского, нормированное пространство, теорема о норме, неравенство Минковского (треугольника), понятие угла в Е, теорема Пифагора.
|
|
|
