 |
Определение чистоты химических веществ
|
|
|
|
Дифференциальный термический анализ позволяет с достаточной точностью определять природу и число фаз в смесях природных минералов, руд, солей и т.д. Составляющие механическую смесь компоненты могут быть легко обнаружены по тепловым эффектам, свойственным каждому индивидуальному веществу, так как тепловые эффекты остаются неизменными, если компоненты смеси не вступают в химическое взаимодействие. Исключением являются эффекты плавления и кипения, которые во многом зависят от наличия примесей и поэтому не могут служить целям идентификации того или иного вещества в смеси. В случае совпадения некоторых температурных эффектов на термограммах солевых смесей, эти вещества могут быть идентифицированы по другим эффектам (разложение, полиморфные превращения и т.д.), являющимся наиболее типическими для данных веществ. Если компоненты системы образуют друг с другом химические соединения, то это приводит к изменению характера термограмм, появлению экзоэффектов и исчезновению эффектов, присущих отдельным веществам. Такое взаимодействие также может оказаться весьма ценным для качественного определения отдельных фаз и превращений в сложной системе.
При качественном фазовом анализе желательно, чтобы термические эффекты, присущие различным веществам, при незначительной разнице в температурах тепловых эффектов не налагались друг на друга. Это может быть, во-первых, достигнуто изменением скорости нагрева. Увеличение скорости нагрева способствует более резкому выявлению термических эффектов. Этому же способствует и уменьшение навесок исследуемых веществ.
Для того, чтобы по площади пиков на дифференциальной кривой судить о количестве поглощенного или выделившегося тепла, необходимо прежде всего рассмотреть влияние различных факторов на запись. Очевидно, что увеличение теплоты превращения, увеличение массы реагирующего вещества приводит к увеличению площади пика на дифференциальной кривой. Однако это изменение может зависеть и от других факторов: природы образца и эталона, изменения теплопроводности, скорости нагрева, положения спаев термопары в веществе, формы тигля, степени измельченности вещества, степени набивки в тигле и т.д.
|
|
|
В зависимости от величин теплопроводности образца и эталона возможно отклонение дифференциальной кривой от нулевой линии, при этом площадь пика также не остается постоянной. Чем больше теплопроводность исследуемых веществ, тем меньше пики, соответствующие тепловым эффектам на термограммах, и, следовательно, сопоставление площадей и определение по ним количественного состава смесей или теплот реакций на отдельных термограммах возможно только при условии одинаковых коэффициентов теплопроводности.
В количественном дифференциальном термическом анализе необходимо учитывать количество вещества, а также форму тигля. Наиболее приемлемой является циллиндрическая форма тиглей. С увеличением навески площадь пика пропорционально растет до определенного значения в зависимости от природы образца.
Степень измельчения навески (дисперсность) и набивки ее в тигле влияют на значение площадей пиков косвенно. Чем больше степень дисперсности вещества и слабее утрамбовка последнего в тигле, тем меньше окажется и общая теплопроводность образца.
Таким образом, учитывая все вышесказанное, можно заключить, что на термограммах воспроизводимы не величины самих тепловых эффектов, а их отношение, т.е. измерения соотношения площадей, образованных дифференциальной кривой, могут быть применены для количественного определения находящихся в смеси веществ.
|
|
|
Отклонение ДТА-кривой от нулевой линии вызвано термическим эффектом в результате реакции, происходящей в образце при его нагреве, а величина площади под кривой ДТА зависит главным образом от разности температур между образцом и эталоном, которая возникает в результате термической реакции. Площадь поверхности под ДТА-кивой определяется следующим соотношением:
, (1)
где: m – масса образца (г); DH – теплота реакции (Дж); l - коэффициент теплопроводности (Дж/град.×с); g – коэффициент, определяемый геометрической формой тигля (см).
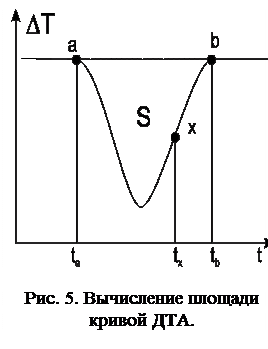
Во время нагрева и протекания реакции в образце в точке x уравнение теплового баланса, начиная с точки a (рис. 5), будет иметь следующий вид:
. (2)
Это означает, что изменение всей энтальпии образца равняется количеству тепла, поглощенного (выделенного) за время dt, плюс количество тепла, полученного образцом от печи за время нагрева dt.
Для эталона уравнение теплового баланса будет иметь вид:
, (3)
где: dH – поглощенная теплота в Дж/г в течение времени dt; m – масса реагирующего вещества в образце; m1 – общая масса образца; m2 – общая масса эталона; K1 и K2 – коэффициенты теплообмена для образца и эталона; T – температура в печи в момент времени tx; T1 и T2 – температуры соответственно для образца и эталона в момент времени tx; T0 – температура образца в момент времени ta; с1 и с2 – средние теплоемкости между ta и tx для образца и эталона.
Запись кривой ДТА экспериментально осуществляется так, чтобы образец и эталон имели одну и ту же массу и одинаковые теплоемкости. В таком случае можно сказать, что m1×c1 = m2×c2. Образец и эталон в виде порошка должны помещаться в тигли одной и той же геометрической формы и размера, и при этом допускается, что K1 = K2 = K.
Если теперь вычесть уравнение (3) из (2), получится:
, (4)
где DT = T1-T2.
Интегрируя в пределах от a до b полученное уравнение при T1-T2 = 0, получим:
, (5)
где: S – площадь пика ДТА-кривой, соответствующая термическому эффекту (град.×с); K – коэффициент теплообмена, состоящий из двух параметров: K = l×g.
Полученное уравнение является основным уравнением, по которому рассчитывают количества тепла в термических методах. Из этого уравнения видно, что площадь пика кривой ДТА пропорциональна массе термоактивного вещества с определенным значением DH и для определенных формы и размера тигля. Эта пропорциональность будет нарушаться, если теплопроводность вещества будет меняться во время нагрева или от опыта к опыту. Необходимо отметить, что коэффициент K в практике термического анализа лучше всего определяется экспериментальным путем для конкретной термической установки посредством построения калибровочной кривой.
|
|
|
Практически величину K при данной температуре определяют следующим образом: сначала записывают кривую ДТА плавления известного калибровочного вещества, измеряют площадь пика под кривой ДТА и рассчитывают по уравнению (5). Точное знание K для каждой температуры определяется как средняя величина из 5 – 12 опытов. Ошибка, как правило, не превышает 0,5 – 5 % в зависимости от типа прибора ДТА. Величина K не является постоянной, а зависит от выбранного диапазона температур, ЭДС используемых термопар, и поэтому калибровочный график K = f(T) не строго линейный и приближается к параболе:
, (6)
где: A – коэффициент, зависящий от величины теплопередачи по проводам термопар и от теплопередачи между тиглями и стенками блока; B – коэффициент, зависящий от радиации.
Необходимо подчеркнуть, что калибровочная кривая пригодна только для конкретного прибора. Если прибор имеет две печи (дериватограф), то калибровку следует проводить для каждой печи отдельно.
В настоящее время для калибровки приборов ДТА, т.е. определения коэффициента K, существуют две методики: метод определения K по энтальпиям плавления калибровочных веществ; электрический метод определения K по эффекту Джоуля. Считается, что самый надежный метод установления K – экспериментальное определение его через теплоты плавления чистых химических веществ, изменение энтальпии (DH) которых хорошо известны. Температуры и теплоты плавления некоторых веществ приведены в таблице 1.
Таблица 1.
Характеристика некоторых калибровочных веществ.
| Вещество | TПЛ, °С | Теплота плавления DH, кДж/моль |
| Бензофенон Дифенил Нафталин Бензойная кислота BiCl3 SnCl2 NaNO3 NaOH KNO3 KOH AgCl LiBr NaJ KCl CaCl2 NaCl LiF Na2SO4 BaCl2 K2SO4 FeS | 48,21 71,0 80,28 122,5 233,0 247,0 306,5 322,0 334,5 405,0 455,0 550,0 661,0 716,0 772,0 801,0 848,0 884,0 960,0 1069,0 1193,0 | 16,7 18,6 18,98 18,0 23,6 12,6 15,1 6,4 9,8 9,4 13,2 17,65 23,7 26,3 28,0 28,2 27,07 24,3 15,9 36,8 32,4 |
При термическом анализе и определении теплот реакций измеряются площади, образо-ванные отклонением ДТА-кривой от своего направления, установившегося в отсутствии эффекта. Если дифференциальная кривая после эффекта является продолжением записи до этого эффекта, то ограничение площади осуществляется очень просто: проводят прямую, соединяющую начало и конец отклонения дифференциальной записи (рис. 8).
|
|
|
Но иногда в процессе реакции может произойти значи-тельное изменение условий теплопередачи в образце. Потеря массы образца, например, при диссоциации или дегидратации должна привести к уменьшению теплоемкости и, следовательно, к соответствующему повышению температуры навески. На дифференциальной кривой это вызовет некоторое отклонение вверх. Далее запись может идти параллельно первоначальному направлению, но на другом уровне, т.е. на другом расстоянии от нулевой линии.
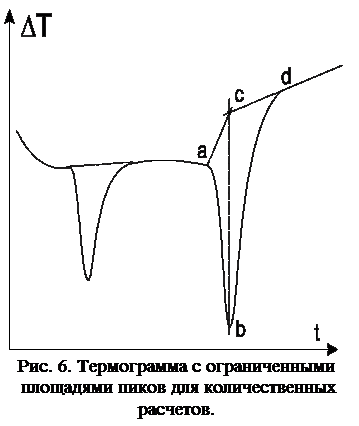Если процесс сопро-вождается изменением тепло-передачи, т.е. дифференциаль-ная запись после эффекта не является прямым продол-жением кривой до него, то это изменение должно найти свое отражение лишь в первой стадии процесса (рис. 6). Тогда в максимуме отклонения дифференциальной кривой, соответствующем окончанию процесса, восстанавливают перпендикуляр bc к оси времени и продолжают прямую установившегося направления дифференциальной записи после реакции до пересечения с перпендикуляром bc. Точка пересечения соединяется прямой с началом отклонения дифференциальной кривой (точка a). При таком способе ограничения площадей увеличение количества новой фазы с иной теплопроводностью и уменьшение прежней фазы отразятся на термограмме наклонной линией именно во время самого процесса, так как возвращение дифференциальной кривой к прежнему направлению соответствует только выравниванию температур образца и эталона после окончания реакции.
Другое затруднение при измерении площадей заключается в разделении площадей двух эффектов, частично накладывающихся друг на друга, причем дифференциальная кривая после первого отклонения не успевает возвратиться к прежнему положению (до реакции) и начинает показывать новое отклонение, соответствующее второму эффекту (рис. 7). В данном случае можно значительно уменьшить, а иногда вообще исключить наложение площадей двух эффектов проведением более медленного нагрева или уменьшением навески вещества. Если же эффекты все-таки наложены друг на друга, полученные площади можно разделить. Предположим, что второго эффекта не было: тогда ограничиваем сверху всю площадь прямой ac и проводим вторую прямую bd, являющуюся продолжением прямолинейного участка возвращения дифференциальной записи после первого эффекта, до пересечения с первой линией ac. Таким образом, получается площадь первого эффекта. Вся остальная площадь будет соответствовать второму эффекту. Ограничение площадей пиков сверху необходимо осуществлять так же, как в предыдущих примерах. Очевидно, что чем больше накладываются эффекты один на другой, тем менее точными получаются результаты, однако все же не настолько, чтобы этим способом нельзя было пользоваться.
|
|
|
Измерения площадей на термограммах для количественных расчетов можно проводить различными методами. Наиболее распространенными являются метод планиметра, метод трапеций, метод взвешивания, метод геометрических построений, методы электромеханического или электронного интегрирования при записи термограмм.
Определение чистоты химических веществ
Методом ДТА
Термические методы определения примесей в твердых телах основаны на точном измерении температуры плавления, которая является характерной физико-химической константой и приводится в справочной литературе. Температура плавления снижается даже при незначительном количестве примесей. На этом принципе понижения точки плавления твердого вещества с очень незначительным содержанием примесей (0,005 %) по отношению к тому же самому чистому химическому соединению основывается криоскопический метод определения чистоты. В криоскопических расчетах применяется известное уравнение Рауля и Вант-Гоффа:
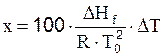, (7)
где: x – мольная доля примеси в идеальной жидкой фазе; DT – понижение (депрессия) температуры плавления по отношению к чистому веществу, К; DHf – теплота (энтальпия) плавления чистого вещества, Дж/моль; R – универсальная газовая постоянная; T0 – температура плавления чистого вещества, К.
Плавление твердых веществ является фазовым переходом первого рода (инвариантный процесс), сопровождающимся эндотермическим эффектом, который четко регистрируется на кривой ДТА. На рис. 8 показана типичная кривая ДТА плавления чистого вещества (99,99 %), которое происходит в очень узком интервале температур.
Величина площади, как известно, пропорциональна энтальпии плавления. Если вещество содержит примеси, то, в зависимости от их количества, точка плавления на температурной шкале будет смещена в область более низких температур, а внешний вид кривой ДТА будет более пологий (рис. 8). Таким образом, уже только по виду кривых ДТА для чистого вещества и того же самого вещества с добавкой разного количества примесей можно судить о чистоте изучаемых веществ. Поскольку определение чистоты основано на измерении точной температуры плавления (±0,1–0,2°С), большое значение приобретает корректность экспериментального ее определения.
Применение уравнения (7) ограничено следующими условиями:
1. основное вещество и вещество-примесь растворимы в жидком состоянии и совершенно нерастворимы в твердом состоянии;
2. изучаемое вещество и примесь образуют идеальный раствор, но не образуют между собой твердые растворы;
3. количество примеси, как правило, должно быть незначительным (менее 5 %);
4. твердая и жидкая фазы находятся в термодинамическом равновесии.
Количество примеси в мольных долях может быть определено, если известен молекулярный вес изучаемого вещества и точная масса самого образца.
|
|
|
