 |
Обратная матрица. Единственность. Существование и вычисление обратной матрицы (через построение и присоединение матрицы).
|
|
|
|
Матрицы. Виды матриц. Равенство матриц, сложение, умножение матрицы на число. Основные свойства
1.1 Матрица - носитель информации, таблица чисел. В теории систем линейных уравнений и дифференциальных уравнений и других материальных объектов большую роль играют матрицы. С их помощью можно не только компактно записать систему уравнений, но и приводя определенные действия решать сами уравнения.
1.2 Матрицы бывают: квадратной (число столбцов равно числу строк), нулевой (все элементы =0), вектор - строкой (состоит из одной строки), вектор-столбец (состоит из одного столбца), диагональной (все элементы, кроме главной диагонали, = 0), единичной (диагональные элементы= 1 “Е”), верхней треугольной (все элементы ниже главной диагонали =0), нижней треугольной (все элементы выше главное диагонали =0), диагональной (одновременно верхне и нижнетреугольная матрица), ступенчатой (если матрица содержит нулевую строку, то все строки, расположенные под нею, также нулевые. П ервый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем i).
1.3 Равенство матриц. Две матрица А и В называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны.
1.4 Сложение матриц. Действие “+” и “-“ над матрицами одинакового размера определяется матрицами, т.е. при “+” или “-“ матрицы “+”/”-“ их элементы находящиеся на одинаковых местах.
1.5 Умножение матрица на число. Произведением матрицы на число называется матрица, у которой все элементы умножены на это число.
1.6 Основные свойства. См. на обратной стороне
|
|
|
Умножение матриц и его свойства. Транспортирование матриц и его свойства.
2.1 Результатом умножения матриц Am×n и Bn×k будет матрица Cm×k такая, что элемент матрицы C, стоящий в i-той строке и j-том столбце (cij), равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:
cij = ai1 · b1j + ai2 · b2j +... + ain · bnj
2.2 См. на обр. стороне
2.3 Транспонирование - это замена строк столбцами. Свойства
· Двойное транспонирование возвращает исходную матрицу: (А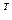 
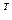) = А.
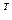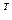· Транспонирование суммы матриц эквивалентно сумме транспонированных слагаемых: (А+В) =А +В .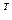
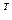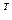· Транспонирование произведения двух матриц эквивалентно произведению транспонированных матриц, взятых в обратном порядке: (АВ) = В А .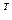
· Произведение матрицы на свою транспонированную: А 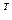А или АА 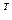всегда имеет результатом симметричную квадратную матрицу.
· Если матрица А - квадратная, то значение ее определителя не зависит от транспонирования: D(A)=D(A ).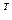
Определители. Свойства определителей.
3.1 Определитель матрицы или детерминант матрицы - это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.
Свойства определителей.
· Определитель единичной матрицы равен единице.
· Определитель матрицы с двумя равными строками (столбцами) равен нулю.
· Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
· Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
· Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
· При транспонировании значение определителя матрицы не меняется: det(A) = det(AT)
· Определитель обратной матрицы: det(A-1) = det(A)-1
· Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
|
|
|
· Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
· Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
· Общий множитель в строке (столбце) можно выносить за знак определителя:
· Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени: B = k·A => det(B) = kn·det(A), где A матрица n×n, k - число.
· Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
· Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
· Определитель произведения матриц равен произведению определителей этих матриц: det(A·B) = det(A)·det(B)
Обратная матрица. Единственность. Существование и вычисление обратной матрицы (через построение и присоединение матрицы).
4.1 Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E: Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.
Единственность.
4.3 Присоединение матрицы. Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной. Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.
4.4 Союзная матрица. Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A, называется союзной матрицей.
|
|
|
