Качество, ценность и стоимость изделия

Для того, чтобы удовлетворять потребности человека, изделие должно иметь определенные свойства, а степень соответствия между свойствами изделия и удовлетворяемыми с его помощью потребностями определяет качество изделия. В настоящее время мерой качества изделий служит степень удовлетворенности потребителя изделием, определяемая соотношение стоимости и ценности (потребительной стоимости) изделия:

{Качество} = {Удовлетворенность потребителя} = {Ценность} / {Cтоимость}

Эти соотношения для производителя и потребителя изделий приведены на Рис.3.

Рис.3. Качество продукции с точки зрения производителя и потребителя

Для производителя вся продукция, не содержащая дефектов, которые препятствовали бы продаже этой продукции, имеет ценность. Для потребителя же ценность имеют только те свойства продукции, которые соответствуют его ожиданиям. Для нас важны три основные соотношения между ценностью и стоимостью:

• между ценностью и стоимостью продукции для потребителя (Q);
• между ценностью и стоимостью продукции для производителя (Q_П);
• между ценностью для потребителя и производителя (К); данное соотношение в значительной мере определяет конкурентоспособность производства.

Рассмотрим, как изменялись эти соотношения в процессе развития производства в 20-м веке.

 

1. Концепции предпринимательства и качества. Риски выбора альтернатив при управлении.

В предпринимательской деятельности всегда присутствуют внутренние и внешние цели. Внутренние цели ставит перед собой предприниматель, начиная или развивая дело. Они, как правило, личные - увеличение собственного дохода, удовлетворение каких - то личных амбиций и склонностей и т.д. Внешние цели предпринимательства - это те цели, на которые рассчитывает общество, разрешая предпринимателю его деятельность. Для общества недостаточно, чтобы предприниматель только отчислял ему определенную долю прибыли в виде налогов, для него необходимо, чтобы деятельность предпринимателя помогала решать те задачи, которое общество перед собой ставит.

В самом общем смысле, эти задачи связаны с повышением качества жизни в обществе, исходя из того, что само общество под таким качеством понимает. Деятельность предпринимателя всегда социальна, и в развитом обществе сам предприниматель это прекрасно осознает. Он строит свою деятельность на основе философии предпринимательства - концепции, описывающие наиболее общие принципы, подходы к производству изделий и услуг, управлению таким производством, взаимоотношениям между предпринимателем, сотрудниками предприятия, обществом, государством, природной средой. Философия предпринимательства основывается на культурных и национальных традициях, общих концепциях развития технической цивилизации. Важнейшей составной частью философии предпринимательства является философия качества, которая также имеет социальную направленность. Посмотрим, как определяется содержание современного менеджмента качества в соответствии с международным стандартом ИСО 8402:

"Метод управления организацией, основанный на сотрудничестве всех ее работников, ориентированный на качество и обеспечивающий через удовлетворение запросов потребителей, достижение целей долговременного предпринимательского успеха и выгоды для всех работников организации и хозяйства в целом".

Примечание 1. “всех ее работников” означает весь персонал организации, на всех уровнях иерархии ее организационной структуры.

Примечание 2. Существенным для обеспечения успеха данного метода является убежденное и упорное руководство со стороны высшей администрации и обучение и переподготовка всех работников организации.

Примечание 3. Термин “качество” при тотальном менеджменте качества вбирает в себя и достижение всех целей менеджмента.

Примечание 4. “выгоды для... хозяйства в целом” означает выполнение требований всех субъектов хозяйства.”

В этом определении мы видим, как увязываются в одно целое успех предпринимателя, выгоды для сотрудников предприятия, - наемных работников, не являющихся собственниками, - и выгоды для общественного хозяйства в целом. Практика показывает, что только при таком гармоничном согласовании интересов всех участников предпринимательской деятельности достигается устойчивый долговременный успех.

В современных промышленно-развитых странах в начале 20-го века начала складываться философия предпринимательства, основанная на концепции так называемого "общества потребления", т.е. общества, целью существования которого является удовлетворение потребностей сограждан. Окончательно эта концепция общества была сформулирована в 50-х годах. Важнейший вклад в воплощение этой концепции в жизнь внес президент США Джон Фицжеральд Кеннеди, выдвинувший в начале 60-х годов концепцию государственной защиты прав потребителя. Согласно этой концепции, государство обязано активно вмешаться во взаимоотношения производителя товаров и услуг и потребителя на стороне последнего, ограждая его от недоброкачественной продукции и взяв на себя защиту его прав. Был принят закон о защите прав потребителей.

Главной фигурой такого общества является потребитель. Его требования (если они социально безопасны) обладают приоритетом над возможностями производителя, и защищаются установлениями государства и общества. Важнейшими достижениями "общества потребления" могут считаться:

• последовательное претворение в жизнь идей свободы торговли, что привело к созданию международного рынка товаров и услуг - потребитель в любой стране может приобретать товар, произведенный в любой стране; следствием этого является резкое обострение конкуренции производителей, обострение их борьбы за повышение качества продукции и конкурентные цены, за снижение сроков выхода товара на рынок и в то же время усиление кооперации и сотрудничества в производстве и продвижении товаров на рынок;
• развитие систем государственной и общественной защиты прав потребителей на качественную продукцию и услуги; эти системы защиты не только позволяют потребителю взыскивать с производителя ущерб за недоброкачественную продукцию и услуги, но и предупреждают появление такой продукции на рынке, а также ограничивают монополизацию рынка производителем; следствием этого является необходимость производителя предоставлять потребителю систему доказательств качества товара еще до того, как потребитель этот товар приобрел;
• достаточно высокий уровень самосознания потребителей, которые согласны платить за качество и готовы сотрудничать с производителем в его повышении.

Несмотря на всю привлекательность концепции "общества потребления", к 90-м годам стало ясно, что неконтролируемый рост потребностей может привести, по крайней мере, к серьезным нарушениям свойств окружающей среды, и даже вызвать экологическую катострофу. Ресурсы Земли не рассчитаны на то, чтобы в "общество потребления" вошла большая часть населения планеты. В то же время концепция развития большинства государств направлена именно на вхождение в "общество потребления" (Россия - не исключение). Поэтому в ближайшее время будет развиваться какая-то новая философия предпринимательства и, соответственно, новая философия качества. Отдельные черты новой философии качества проявляются уже сейчас, например, в концепции экологического менеджмента и в концепции производственной системы "Тойота".

Таким образом, в соответствии с существующей философией предпринимательства, вся полнота ответственности за качество изделий и услуг лежит на производителе. Производитель в разные исторические промежутки по-разному реагировал на эту ответственность, воплощая различные философии обеспечения качества.

Статистические методы в управлении качеством
(проф. Скачко Ю.В.)

1. Семь инструментов контроля качества. Расслоение, графики. Диаграмма Парето. Гистограмма. Диаграмма разброса. Графики. Примеры.

Контрольный листок - инструмент для сбора данных и их автоматического упорядочения для облегчения дальнейшего использования собранной информации.

Гистограмма - инструмент, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания данных в определенный (заранее заданный) интервал.

Диаграмма Парето - инструмент, позволяющий объективно представить и выявить основные факторы, влияющие на исследуемую проблему, и распределить усилия для ее эффективного разрешения.

Метод стратификации (расслаивания данных) - инструмент, позволяющий произвести разделение данных на подгруппы по определенному признаку.

Диаграмма разброса (рассеивания) - инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.

Диаграмма Исикавы (причинно-следственная диаграмма) - инструмент, который позволяет выявить наиболее существенные факторы (причины), влияющие на конечный результат (следствие).

Контрольная карта - инструмент, позволяющий отслеживать ход протекания процесса и воздействовать на него (с помощью соответствующей обратной связи), предупреждая его отклонения от предъявленных к процессу требований.

 

 

Контрольные листы (или сбор данных) – специальные бланки для сбора данных. Они облегчают процесс сбора, способствуют точности сбора данных и автоматически приводят к некоторым выводам, что очень удобно для быстрого анализа. Результаты легко преобразуются в гистограмму или диаграмму Парето. Контрольные листки могут применяться как при контроле по качественным, так и при контроле по количественным признакам. Форма контрольного листа может быть разной, в зависимости от его назначения (рис. 1).

 

Рис. 1 - Примеры контрольного листка

 

Гистограмма

Гистограмма – вид столбцовой диаграммы. Служит для обобщения цифровых данных. Может быть использована как средство графического отображения данных контрольного листа. Характер распределения полученных данных может обнаружить суть проблемы. Предназначена для коммуникации непосредственно с людьми, управляющими процессом. Гистограмма отображает зависимость частоты попадания параметров качества изделия или процесса в определенный интервал значений от этих значений.

Гистограмма строится следующим образом (рис. 2):

1. Определяем наибольшее значение показателя качества.
2. Определяем наименьшее значение показателя качества.
3. Определяем диапазон гистограммы как разницу между наибольшим и наименьшим значением.
4. Определяем число интервалов гистограммы. Часто можно пользоваться приближенной формулой: (число интервалов) = Ц (число значений показателей качества) Например, если число показателей = 50, число интервалов гистограммы = 7.
5. Определяем длину интервала гистограммы = (диапазон гистограммы) / (число интервалов).
6. Разбиваем диапазон гистограммы на интервалы.
7. Подсчитываем число попаданий результатов в каждый интервал.
8. Определяем частоту попаданий в интервал = (число попаданий)/(общее число показателей качества)
9. Строим столбчатую диаграмму.

 

Рис. 2 - Гистограмма потребления топлива для 100 автомобилей

 

Диаграмма Парето

 

Анализ Парето получил свое название по имени итальянского экономиста Вилфредо Парето, который показал, большая часть капитала (80%) находится в руках незначительного количества людей (20%). Парето разработал логарифмические математические модели, описывающие это неоднородное распределение, а математик М.Оа. Лоренц представил графические иллюстрации.

Правило Парето - "универсальный" принцип, который применим во множестве ситуаций, и без сомнения - в решении проблем качества. Джозеф Джуран отметил "универсальное" применение принципа Парето к любой группе причин, вызывающих то или иное последствие, причем большая часть последствий вызвана малым количеством причин. Анализ Парето ранжирует отдельные области по значимости или важности и призывает выявить и в первую очередь устранить те причины, которые вызывают наибольшее количество проблем (несоответствий).

Анализ Парето как правило иллюстрируется диаграммой Парето, на которой по оси абсцисс отложены причины возникновения проблем качества в порядке убывания вызванных ими проблем, а по оси ординат - в количественном выражении сами проблемы, причем как в численном, так и в накопленном (кумулятивном) процентном выражении.

На диаграмме отчетливо видна область принятия первоочередных мер, очерчивающая те причины, которые вызывают наибольшее количество ошибок. Таким образом, в первую очередь, предупредительные мероприятия должны быть направлены на решение проблем именно этих проблем (рис. 3).

 

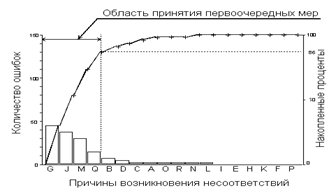
Рис. 3 - Диаграмма Парето

Метод стратификации

 

В основном, стратификация - процесс сортировки данных согласно некоторым критериям или переменным, результаты которого часто показываются в виде диаграмм и графиков

Мы можем классифицировать массив данных в различные группы (или категории) с общими характеристиками, называемыми переменной стратификации. Важно установить, которые переменные будут использоваться для сортировки.

Стратификация - основа для других инструментов, таких как анализ Парето или диаграммы рассеивания. Такое сочетание инструментов делает их более мощными (рис. 4).

На рисунке приведен пример анализа источника возникновения дефектов. Все дефекты (100%) были классифицированы на четыре категории - по поставщикам, по операторам, по смене и по оборудованию. Из анализа представленных донных наглядно видно, что наибольший вклад в наличие дефектов вносит в данном случае «поставщик 1».

 

Рис. 4 - Стратификация данных

 

Диаграмма разброса

Диаграмма (график) разброса - показывает характер взаимоотношений между двумя переменными. Закономерности взаимосвязи могут как проявляться, так и отсутствовать вообще. Необработанные данные изображаются как функция двух переменных, между которыми затем может обнаружиться взаимосвязь. Например, существует ли зависимость между температурой окружающей среды и числом простудных заболеваний? Если падает температура, растет ли число заболеваний? Чем ближе точки располагаются к диагональной линии, тем более четко существует прямая зависимость двух указанных параметров. Взаимосвязь может быть положительной, отрицательной, либо отсутствовать вообще.

Если взаимосвязь будет установлена, то это облегчит определение сути проблемы (рис. 5).

 

Рис. 5 - Диаграмма разброса: имеется прямая взаимосвязь между показателями качества

 

Диаграмма Исикавы

Причинно-следственная диаграмма (диаграмма Исикавы, «рыбий скелет»)- демонстрирует отношения между проблемой и ее возможными причинами. Обеспечивает модель установления связей между проблемой и факторами, влияющими на нее. Причинно-следственная диаграмма полезна для устранения причин появления проблем, а также полезна для понимания эффектов воздействия нескольких факторов на процесс. Анализируется четыре основных причинных фактора: человек, машина (оборудование), материал и метод работ. При анализе этих факторов выявляются вторичные, третичные и т.д. причины, приводящие к дефектам и подлежащие устранению. Для анализа дефектов и построения диаграммы необходимо определить максимальное число причин, которые могут иметь отношение к допущенным дефектам. Такую диаграмму еще называют диаграммой «четыре М» по составу основных факторов (рис. 6).

 

Рис. 6 - Пример диаграммы Исикавы

 

Контрольная карта

Контрольные карты - специальный вид диаграммы, впервые предложенный В. Шухартом в 1925 г. Контрольные карты имеют вид, представленный на рис. 7. Они отображают характер изменения показателя качества во времени.

 

Рис. 7 - Общий вид контрольной карты

Контрольные карты по количественным признакам - это как правило сдвоенные карты, одна из которых изображает изменение среднего значения процесса, а 2-я - разброса процесса. Разброс может вычисляться или на основе размаха процесса R (разницы между наибольшим и наименьшим значением), или на основе среднеквадратического отклонения процесса S. В настоящее время обычно используются x - S карты, x - R карты используются реже.

Контрольные карты по качественным признакам (рис. 8):

Карта для доли дефектных изделий (p-карта). В p-карте подсчитывается доля дефектных изделий в выборке. Она применяется, когда объем выборки - переменный.

Карта для числа дефектных изделий (np-карта). В np-карте подсчитывается число дефектных изделий в выборке. Она применяется, когда объем выборки - постоянный.

Карта для числа дефектов в выборке (с-карта). В с-карте подсчитывается число дефектов в выборке.

Карта для числа дефектов на одно изделие (u-карта). В u-карте подсчитывается число дефектов на одно изделие в выборке.

 

1. Числовые характеристики случайных величин. Моменты распределения. Описательная статистика в Excel.

 

Математическое ожидание. Математическим ожиданием дискретной случайной величины Х, принимающей конечное число значений хi с вероятностями рi, называется сумма:

(6 а)

Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f (x):

(6 б)

Несобственный интеграл (6 б) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М (Х) не существует). Математическое ожидание характеризует среднее значение случайной величины Х. Его размерность совпадает с размерностью случайной величины.

Свойства математического ожидания:

(7)

 

Дисперсия. Дисперсией случайной величины Х называется число:

(8)

Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М (Х). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:

(9)

Здесь m = М (Х).

Свойства дисперсии:

(10)

Среднее квадратичное отклонение:

(11)

Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.

Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0называется математическое ожидание М (Х – х 0) k. Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:

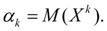(12)

Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:

(13)

Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:

(14)

Из (7) следует, что центральный момент первого порядка всегда равен нулю:

(15)

Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С).
Теперь очевидно, что дисперсия – это центральный момент второго порядка:

(16)

 

Асимметрия. Центральный момент третьего порядка:

(17)

служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии:

(18)

Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).

Рис. 2. Виды асимметрии распределений.

 

Эксцесс. Центральный момент четвертого порядка:

(19)

служит для оценки так называемого эксцесса, определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения , то в качестве эксцесса принимается величина:

(20)

На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).

 

Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.

Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным. Если кривая распределения имеет более одного максимума, то распределение называется полимодальным. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.

Медиана случайной величины Х – это ее значение Ме, для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме. Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.

 

1. Гистограмма закона распределения. Нормальное распределение. Доверительный интервал. Последовательность анализа качества посредством гистограммы. Плотность распределения и технологический допуск.

 

 

1. Статистические методы и метрологическое обеспечение в управлении качеством. Методы уменьшения случайной погрешности средств измерений.

 

 

1. Измерения с многократными наблюдениями как пример использования статистических методов. Результат измерений.

 

 

1. Регрессионный анализ в задачах управления качеством. Инструменты качества для уменьшения систематической погрешности измерений:

1. Метод инвертирования широко используется для устранения ряда постоянных и медленно изменяющихся систематических погрешностей. Этот метод и ряд его разновидностей (метод исключения погрешности по знаку, коммутационного инвертирования, структурной модуляции, двукратных измерений, инвертирования функции преобразования и др.) основаны на выделении алгебраической суммы чесного числа сигналов измерительной информации, которые вследствие инвертирования отличаются направлением информативного сигнала, опорного сигнала или знаком погрешности.

2. Метод модуляции - метод близкий к методу инвертирования, в котором производится периодическое инвертирование входного сигнала и подавление помехи, имеющей однонаправленное действие.

3. Метод исключения погрешности по знаку - вариант метода инвертирования, который часто применяется для исключения изввестных по природе погрешностей, источники которых имеют направленное действие, например погрешностей из-за влияния постоянных магнитных полей, ТЭДС и др.

4. Метод замещения (метод разновременного сравнения) является наиболее универсальным методом, который дает возможность устранить большинство систематических погрешностей. Измерения осуществляются в два приема. Сначала по отсчетному устройству прибора делают отсчет измеряемой величины, затем, сохраняя все условия эксперимента неизменными, вместо измеряемой величины на вход прибора подют изместную величину, значение которой спомощью регулируемой меры (калибратором) устанавливают таким образом, чтобы показание прибора было таким же, как при включении измеряемой величины.

5. Метод равномерного компарирования является разновидностью метода замещения, он используется при измерениях таких ввеличин, которые нельзя с высокой точностью воспроизводить с помощью регулируемых мер или других технических средств. Обычно это величины, изменяющиеся с высокой частотой или по сложному закону. В качестве измпестных регулируемых величин при этом используются величины такого же рода, как измеряемые, но отличаютщиеся от них спектральным составом (обычно постоянные во времени и в пространстве) и создающие такой же, как и измеряемая величина, сигнал на выходе компарирующего преобразователя.

6. Метод эталонных сигналов заключается в том, что на вход средств измерений периодически вместо измеряемой величины подаются эталонные сигналы такого же рода, что и измеряемая величина. Разность между реальной градуировочной характеристикой используется для коррекции чувствительности или для автоматического введения поправки в результат измерения. При этом, как и при методе замещения, устраняютсявсе систематические погрешности, но только в тех точках диапазона измерений, которые соответствуют эталонным сигналам. Метод широко используется в современных точных цифровых приборах и в информационно-измерительных системах. Пример использования этого методаявляется периодическая подстройка рабочего тока в компенсаторах и цифровых вольтметрах постоянного тока при помощи нормального элемента.

7. Тестовый метод - при использовании данного метода значение измеряемой величины определяется по результатам нескольких наблюдений, при которых в одном случае входным сигналом средства измерений является сама измеряемая величина Х, а в других - так называемые тесты, являющиеся фукциями измеряемой величины.

8. Метод вспомагательных измерений используется для исключения погрешностей из-за влияющих величин и неинформативных параметров входного сигнала. Для реальзации этого метода одновременно с измеряемой величиной Х с помощью вспомогательных измерительных устройств производится измерение каждой из влияющих величин и вычисление с помощью вычислительного устройства, а также фомул и алгорптмов поправок к резульататм измерения.

9. Метод симметричных наблюдений заключается в проведении многократных наблюдений через равные промежутки времени и усреднении результатов наблюдений, симметрично расположенных относительно среднего наблюдения. Обычно этот метод применяется для исключения прогрессирующих погрешностей, изменяющихся по линейному закону. Так, при измерении сопротивления резистора путем сравнения напряжения на измеряемом и эталонном резисторах, включенных последовательно и питаемых от общего аккумулятора, может возникнуть погрешность вследствие разряда источника питания.

 

 

1. Коэффициент точности и брак. Процент брака и процент годных изделий. Функция Лапласа для оценки качества. Примеры.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: