ГЛАВА 2. Линейно упорядоченное пространство ординальных чисел.

ЛИНЕЙНО УПОРЯДОЧЕННОЕ ПРОСТРАНСТВО ОРДИНАЛЬНЫХ ЧИСЕЛ

 

 

                                                                   Выполнила студентка 5 курса

математического факультета Лоптева О. Н.

_____________________________/подпись/

 

Научный руководитель:

к.ф.-м.н., доц. Варанкина В. И.

_____________________________/подпись/

 

Рецензент:

к.ф.-м.н., доц. Здоровенко М. Ю.

_____________________________/подпись/

 

Допущена к защите в ГАК                                                         

 

Зав. кафедрой_______________________                Крутихина М. В.

                                                                                       «____»______________________________

Декан факультета____________________                Варанкина В. И.

                                                                                       «____»______________________________

 

КИРОВ, 2003

                                      ОГЛАВЛЕНИЕ

 

 

Введение.............................................. 3 

 

Глава 1

Исходные определения

§1. Порядковые определения......................................4

§2. Топологические определения.................................. 5

Глава 2

Линейно упорядоченное пространство ординальных чисел

§1. Вполне упорядоченные множества и их свойства..................8

§2. Конечные цепи и их порядковые типы.......................... 10

§3. Порядковый тип............................................ 11

§4. Свойства ординальных чисел..................................13

§5. Пространство ординальных чисел W( ₁) и его свойства............18

Список литературы.......................................... 25

 

                                            ВВЕДЕНИЕ

 

Идеи топологии были высказаны ещё выдающимися математиками 19 века: Н. И. Лобачевским, Риманом, Пуанкаре, Кантором, Гильбертом и Бауэром. Однако общая топология, как её понимают сейчас, ведёт начало от Хаусдорфа («Теория множеств», 1914).

Истоки теории упорядоченных и частично упорядоченных алгебраических систем лежат в геометрии, функциональном анализе и алгебре.

Линейно упорядоченные пространства, в том числе и линейно упорядоченное пространство ординальных чисел, объединяют в себе две структуры: порядковую и топологическую. Систематического изложения теории пространства ординальных чисел не существует. Этим объясняется актуальность выбранной темы.

Целью дипломной работы является исследование пространства ординальных чисел, его порядковых и топологических свойств. В первой главе будут даны основные понятия теории множеств и общей топологии, а во второй главе будет введено понятие порядкового типа, установлены свойства порядковых чисел, а также проведено исследование пространства ординальных чисел, имеющее важное значение для данной работы. Будет доказана хаусдорфовость, нормальность, локальная компактность, счётная компактность, неметризуемость и некоторые другие свойства линейно упорядоченного пространства ординальных чисел.

      

 

 

                 

ГЛАВА 1. Исходные определения и теоремы.

 

ПОРЯДКОВЫЕ ОПРЕДЕЛЕНИЯ.

Определение 1.1. Упорядоченным множеством называется непустое множество Х вместе с заданным на нём бинарным отношением порядка , которое:

рефлексивно: а a;

транзитивно: a b c a c;

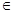антисимметрично: a b a a = b (для любых a, b, c X).

Элементы упорядоченного множества называются сравнимыми, если

а < b, a = b или b < a.

Замечание: по определению будем считать, что a < b, если a b и a   b.

Определение 1.2. Упорядоченное множество называется линейно упорядоченным, или цепью, если любые его два элемента сравнимы.

Определение 1.3. Элемент а упорядоченного множества Х называется наименьшим (наибольшим)  элементом  множества А Х, если а 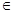А и а  х

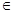 (х  а) для любого х А.

Определение 1.4. Элемент а упорядоченного множества Х называется минимальным (максимальным) элементом множества А Х, если в А нет элементов, меньших (больших) а, то есть если х  а (а  х) для некоторого х , то х = а.

Определение 1.5. Пусть А – непустое подмножество линейно упорядоченного множества Х. Элемент а из Х называется верхней (нижней) гранью множества А, если он больше (меньше) любого элемента из А.

Определение 1.6. Если множество А имеет хотя бы одну верхнюю (нижнюю) грань, то А называется ограниченным сверху (ограниченным снизу).

Определение 1.7. Множество А называется ограниченным, если оно ограничено и сверху и снизу.

Определение 1.8. Точной верхней гранью множества А называется наименьший элемент множества всех верхних граней множества А. Обозначается sup A.

Определение 1.9. Точной нижней гранью множества А называется наибольший элемент множества всех нижних граней множества А. Обозначается inf A.  

Определение 1.10. Пусть < X, > - линейно упорядоченное множество, содержащее,  по  крайней  мере,  два  элемента. Для а, b X, a < b положим

(a, b) = { x X: a < x < b }. Такие множества будем называть интервалами в Х. Множество [ a, b ] = { x X: a x b } называется отрезком в Х.

Определение 1.11. Упорядоченное множество называется вполне упорядоченным, если каждое его непустое подмножество имеет наименьший элемент.

Определение 1.12. Пусть М и М₁ – упорядоченные множества и пусть f – взаимно однозначное отображение М на М₁. Отображение сохраняет порядок, если из того, что a b (a, b M), следует, что f (a) f (b) (в М₁). Отображение f называется изоморфизмом упорядоченных множеств М и М₁, если соотношение f (a) f (b) выполнено в том и только в том случае, если a b. При этом множества М и М₁ называются изоморфными между собой.

§2. ТОПОЛОГИЧЕСКИЕ ОПРЕДЕЛЕНИЯ.

 

Определение 1.13. Топологическим пространством называется пара (Х, ), состоящая из множества Х и некоторого семейства  подмножеств множества Х, удовлетворяющая следующим условиям:

1) множество Х и Æ принадлежат  ;

2) пересечение конечного числа множеств из  принадлежат ;

3) объединение любого числа множеств из  принадлежит .

Условия 1 – 3 называются аксиомами топологического пространства, его элементы – точками пространства. Подмножества множества Х, принадлежащие семейству , называются открытыми в Х. Семейство  открытых подмножеств пространства Х называется также топологией на Х.

Определение 1.14. Замкнутым множеством называется множество, которое является дополнением к открытому.

Определение 1.15. Окрестностью точки х топологического пространства называется любое открытое множество U, содержащее х.

Определение 1.16. Топологическое пространство Х называется компактным, если из любого его покрытия открытыми множествами можно выделить конечное подпокрытие.

Определение 1.17. Топологическое пространство Х называется компактным, если любая его центрированная система замкнутых множеств в Х имеет непустое пересечение.

Определения 1.16 и 1.17 равносильны ([5]).

Определение 1.18. Пространство Х называется локально компактным, если каждая точка имеет окрестность, замыкание которой компактно.

Определение 1.19. Топологическое пространство Х называется счётно компактным, если из каждого счётного открытого покрытия пространства Х можно выбрать конечное подпокрытие.

Определение 1.20. Топологическое пространство Х называется счётно компактным, если каждое его бесконечное подмножество содержит хотя бы одну предельную точку.

Определения 1.19 и 1.20 равносильны ([5]).

Определение 1.21. Пространство  называется компактификацией топологического пространства Х, если:

    1)  компактно;

     2) Х – подпространство ;

     3) Х плотно в .

Определение 1.22. Топологическое пространство Х называется Т₁-пространством, если для каждой пары различных точек х₁, х₂  существует открытое множество 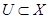, такое, что х₁  и х₂ .

Определение 1.23. Если любые две различные точки х и у топологического пространства Х имеют непересекающиеся окрестности, то пространство Х называется хаусдорфовым пространством или Т₂-пространством.

Определение 1.24. Топологическое пространство Х называется регулярным пространством, или Т₃-пространством, если Х есть Т₁-пространство и для любого  и каждого замкнутого множества , такого, что , существуют открытые множества U ₁ и U ₂, такие, что ₁, ₂ и U ₁ U ₂ = Æ.

Определение 1.25. Топологическое пространство Х называется тихоновским пространством, или Т₃ -пространством, если Х есть Т₁-пространство и для любого  и любого замкнутого множества , такого, что , существует непрерывная функция f: , такая, что f (x)=0 и f (y)=1 для .

Определение 1.26. Топологическое пространство Х называется нормальным, или Т₄-пространством, если для каждой пары непересекающихся замкнутых множеств А и В существуют непересекающиеся открытые множества U и V такие, что А U, B V.

 

ГЛАВА 2. Линейно упорядоченное пространство ординальных чисел.

§1.ВПОЛНЕ УПОРЯДОЧЕННЫЕ МНОЖЕСТВА И ИХ СВОЙСТВА.

Рассмотрим вполне упорядоченные множества и их свойства.

Предложение 1.1. Всякое подмножество вполне упорядоченного множества само есть вполне упорядоченное множество (очевидно).

Предложение 1.2. Если f – изоморфизм вполне упорядоченного множества А в себя, то для любого элемента х А выполняется неравенство f (x) x.                                                                                  (1)                            

Доказательство.

Будем доказывать методом от противного и предположим, что в А есть элементы х, не удовлетворяющие неравенству (1). Тогда среди этих элементов есть наименьший, так как А является вполне упорядоченным. Обозначим его через х₁: f (x ₁)< x ₁. Обозначим f (x ₁) = x ₀ и перепишем неравенство: х₀ < х₁. Так как f – изоморфизм, то выполняется неравенство: f (x ₀)< f (x ₁) = x ₀.

Таким образом, получили следующие неравенства: х₀ < x ₁ и f (x ₀) < x ₀ . Эти неравенства противоречат определению элемента х₁, как наименьшего из элементов х множества А, не удовлетворяющих условию f (x) < x. ■

Определение 2.1. Начальным отрезком, отсекаемым элементом а А от линейно упорядоченного множества А, называется множество А_а = { x | x A, x < a }.

Предложение 1.3. Пусть А’ – произвольное подмножество вполне упорядоченного множества А. Тогда множество А не изоморфно никакому отрезку множества А’.

Доказательство:

Будем доказывать методом от противного и предположим, что существует изоморфизм вполне упорядоченного множества А в некоторый отрезок А_х’ подмножества А’ А. Тогда f (x)   A_x ’. Следовательно, f (x) < x – противоречие с предложением 1.2. ■

Следствие 1.4. Два различных отрезка вполне упорядоченного множества не могут быть изоморфны между собою.

Доказательство.

Пусть А_х и А_у – два различных отрезка вполне упорядоченного множества А. Так как А_х и А_у различны, а множество А – вполне упорядочено, то х и у сравнимы, при этом х у. Пусть для определённости x < y. Тогда А_х – отрезок множества А_у и по предложению 1.3 А_х и А_у не могут быть изоморфными. ■

Предложение 1.5. Существует не более одного изоморфизма одного вполне упорядоченного множества на другое.

Доказательство.

Будем доказывать методом от противного и предположим, что f и g – два различных изоморфизма вполне упорядоченного множества А на вполне упорядоченное множество В. Так как f и g различны, то существует а А: b = f (a)   b ’ = g (a). Пусть для определённости b < b ’. При всяком изоморфизме f множества А на множество В отрезок А_х   А переходит в отрезок В_у  В, где у = f (х). Поэтому отрезок А_а А  подобен отрезкам

В _b  В и В _{b ’} B, т. е. B_b изоморфен A_a и А_а изоморфен В _{b ’}. Следовательно, отрезок В _b  изоморфен отрезку B_{b ’}, но это противоречит следствию 1.4. ■

Определение 2.2.  Если  для  элемента   а  А  существует  элемент   а’ =

= inf { x | a < x, x A }, то а’ называется непосредственно следующим за а.

Предложение 1.6. Если А – вполне упорядоченное множество, то у каждого элемента множества А, кроме наибольшего, имеется непосредственно следующий за ним элемент.

Доказательство.

Возьмём некоторый элемент а А, пусть а не является наибольшим элементом. Рассмотрим множество { x | x A, x > а }. По предложению 1.1 оно имеет наименьший элемент а’, который является точной нижней гранью рассматриваемого множества. Следовательно, а’ следует за а. ■

 

 

            § 2. КОНЕЧНЫЕ ЦЕПИ И ИХ ПОРЯДКОВЫЕ ТИПЫ.

Предложение 2.1. Множество из n элементов можно линейно упорядочить n! способами.

Доказательство.

Для доказательства достаточно применить формулу числа перестановок для n-элементного множества: Р_n=n! ■

Предложение 2.2.  Любое конечное линейно упорядоченное множество является вполне упорядоченным множеством.

Доказательство.

Пусть есть множество А – конечное линейно упорядоченное множество. Надо доказать, что А является вполне упорядоченным, то есть любое его подмножество имеет наименьший элемент. Рассмотрим произвольное множество В, являющееся подмножеством множества А. Предположим, что оно не имеет наименьшего элемента. Возьмём какой-нибудь элемент множества В. Обозначим его через b ₁. Так как в В нет наименьшего элемента, то в нём есть элемент b ₂, такой, что b ₂ < b ₁. Элемент b ₂ не является наименьшим элементом в В, поэтому имеется элемент b ₃ < b ₂. Повторяя это рассуждение, строим для каждого натурального n элемент b _n+1   B, причём b _n+1 < b _n.

Таким образом, получили бесконечное множество { b ₁, b ₂,..., b _n,.. } , но это противоречит тому, что В – подмножество конечного множества А и, следовательно, само является конечным. ■

Предложение 2.3. Любые две конечные цепи, состоящие из n элементов, изоморфны.

Доказательство.

пусть есть две конечные цепи из n элементов:

                         a ₁ < a ₂ <…< a_n,

                         b ₁ < b ₂ <…< b_n.

Для каждого а _i  положим f (a_i) = b_i. Очевидно, что отображение f является изоморфизмом. ■

Замечание: бесконечные линейно упорядоченные множества одинаковой мощности могут и не быть изоморфными. Например, множество натуральных чисел и множество целых чисел с естественными порядками. Мощности этих множеств равны, но они не являются изоморфными, так как в N есть наименьший элемент, а в Z наименьшего элемента нет.

Определение 2.3. Порядковым типом линейно упорядоченного множества А называется класс всех линейно упорядоченных множеств, изоморфных множеству А.

Будем считать, что порядковый тип пустого множества есть 0.

Обозначим через n порядковый тип n – элементного множества

N_n = {0, 1, 2,…, n - 1} с порядком 0 < 1 < 2 <…< n-1.

 

                          §3.ПОРЯДКОВЫЙ ТИП .

Определение 2.4. Множество натуральных чисел с естественным порядком и все изоморфные ему линейно упорядоченные множества называются множествами порядкового типа .

Предложение 3.1. Бесконечное линейно упорядоченное множество А имеет порядковый тип  тогда и только тогда, когда оно удовлетворяет следующим условиям:

1) во множестве А имеется наименьший элемент a ₀;

2) для любого а А существует точная нижняя грань а’ во множестве { x | a < x, x A };

  3) для любого подмножества Х множества А из того, что а₀ Х и Х

содержит вместе с каждым своим элементом непосредственно  следующий за ним элемент, следует, что Х = А.

Доказательство.

 Пусть линейно упорядоченное множество А удовлетворяет условиям 1)- 3). Докажем, что А имеет порядковый тип , то есть А изоморфно множеству N.

Из условия (1) следует существование во множестве А наименьшего элемента а₀.

Рассмотрим отображение f: N   A, заданное таким образом: f (0) = a ₀,

f (n + 1) = (f (n))’, где n = 0, 1, 2,… Существование (f (n))’ для каждого n обеспечивается условием (2). Тогда вследствие условия (3) f (N)= A. Таким образом, f инъективно и сюръективно, следовательно, взаимно однозначно.       Докажем, что f сохраняет порядок: возьмём n, m   N, пусть для определённости n < m.  Из условия  (2)  следует,  что f (n) < (f (n))’   f (m),

то есть f (n) < f (m). Следовательно, f сохраняет порядок.

Таким образом, f – взаимно однозначное отображение N   A, сохраняющее порядок. Следовательно, множество А имеет порядковый тип .

 Пусть есть бесконечное линейно упорядоченное множество А, имеющее порядковый тип . Множество N удовлетворяет условиям 1) – 3), а множество А изоморфно ему, поэтому и множество А удовлетворяет условиям 1) – 3). ■

Определение 2.5. Порядковым типом ^* называется класс линейно упорядоченных множеств, эквивалентных множеству N с двойственным порядком: 1 > 2 > 3 >…

Предложение 3.2. упорядоченное множество является вполне упорядоченным тогда и только тогда, когда оно не содержит подмножество типа ^*.

Доказательство.

 Предположим, что вполне упорядоченное множество А содержит подмножество Х типа ^*. Тогда в Х нет наименьшего элемента, что противоречит вполне упорядоченности множества А. Следовательно, в А нет подмножеств типа ^*.

 Пусть множество А не содержит подмножество типа ^*. Докажем, что А является вполне упорядоченным множеством. Предположим, что это не так, т. е. А содержит подмножество В, в котором нет наименьшего элемента. Возьмём какой-нибудь элемент множества В, обозначим его b ₁. Так как в В нет наименьшего элемента, то существует элемент b ₂ , для которого b ₂ < b ₁. Повторяя это рассуждение, строим для каждого n N элемент b_{n +1}   B, причём:

                                              b_{n +1} < b_n.

Получили множество { b ₁, b ₂, …, b_n,...} которое является подмножеством множества А и имеет тип ^* - противоречие. ■

 

12	Поделиться:

Воспользуйтесь поиском по сайту: