 |
Построение моделей авторегрессионных преобразований.
|
|
|
|
После того как установлено наличие автокорреляции следует приступить к построению модели. Основными моделями связных рядов динамики являются модели авторегрессии, или модели авторегрессионных преобразований. В настоящее время разработано 3 способа исключения автокорреляции:
Основан на использовании, так называемых, последовательных или конечных разностей.
Основан на определении цепных абсолютных (последовательные) или базисных абсолютных (конечных) разностей.
Модель данным методом имеет вид: ∆yt+1 = a0 + a1∆x1, t+1 + a2∆x2, t+1 +... + ak∆xk, t+1.
Сущность метода заключается в последовательном исключении величины предшествующих уровней из последующих:
∆x = xi - xi-1
∆y = yi - yi-1
∆y1 = yt - yt – 1
……………………
∆x1 = xt - xt - 1
∆x2 = xt- 1 - xt- 2
При коррелировании разностей в общем виде функция зависимости результативного признака от факторных может быть представлена в следующем виде: ∆y= f(∆x)
Для парной зависимости модель имеет вид: ∆y t+1 = a0 + a1∆x1, t+1, k – число факторных признаков; a0, a1,…, an– параметры модели регрессии, определяемые путем решения создания следующей системы уравнений:
для парной зависимости:
Показателем тесноты связей между изучаемыми признаками, представленными последовательными разностями, является коэффициент корреляции разностей:
[-1;1]
Интерпретация коэффициентов корреляции разностей аналогична интерпретации парного коэффициента корреляции. (Характеризует степень тесноты связи между двумя метрическими переменными). Чем ближе он по абсолютной величине к 1, тем ближе статистическая зависимость между x и y к линейной функциональной. Положительное значение коэффициента = связь между признаками прямая (с ростом x увеличивается значение y), отрицательное значение – связь обратная.
|
|
|
Метод отклонений эмпирических значений признака от теоретических по уравнению тренда полученных.
Определяется тенденция исходных рядов динамики. Рассчитывается тренд, и его величина исключается из каждого уровня.
Этапы реализации:
1) произвести аналитическое выравнивание каждого из рядов динамики, составляющих анализируемый связный ряд по любому рациональному многочлену;
2) определить величину отклонения каждого фактического уровня ряда динамики от теоретических, полученных по уравнению тренда: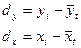 
3) функция зависимости отклонений имеет вид: 
Для парной зависимости модель будет иметь вид:
или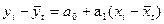 
, где а0 и а1 определяется по формуле:
Модель в общем виде может быть представлена следующим образом:
. Или 
.
Оценка степени тесноты связи осуществляется на основе расчета и анализа коэффициента корреляции отклонений:
Коэффициент корреляции отклонений характеризует степень связи между отклонениями фактических уровней сравниваемых рядов от соответствующих, им выравненных, уровней коррелируемых рядов динамики.
Метод Фриша-Воу
Этот метод заключается в ведении времени как дополнительного факторного признака. В общем виде модель Ф-В имеет вид: 
Даже при наличии парной зависимости при реализации метода Ф-В парные связи обращаются в многофакторные и модель оценки влияния одного фактора на изменение результативного показателя будет иметь вид: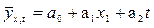 
Параметры данной модели определяются следующим образом:
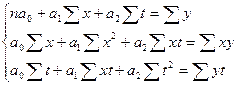
Метод Ф-В заключается в введении времени как дополнительного факторного признака. Это возможно только в случае, если основные тенденции временных рядов одинаковы. В этом случае парные связи обращаются в связи многофакторные и расчеты коэффициента корреляции и уравнения регрессии проводятся методом многофакторной корреляции. Коэффициент корреляции рассчитывается как множественный:
|
|
|
, 
, 
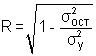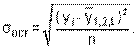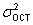— остат. дисперсия; 
— общ. дисперс.
Недостатком 3-х методов является то, что теоретически слабо обоснованы интерпретация и экономическое содержание параметров.
Исходя из этого в рядах динамики, имеющих небольшие периодические колебания, данная методика построения моделей авторегрессионных преобразований не используется. Наибольшее преимущество в экономическом анализе отдается методы Ф-В, т.к. позволяет наиболее точно и без проведения дополнительных вычислительных работ интерпретировать параметры исходной модели. Применение методов авторегрессионных преобразований для анализа связных рядов динамики осложняется наличием временных лагов. Наиболее четко временные лаги прослеживаются в строительстве, при модернизации оборудования и т.д.
Под временным лагом следует понимать несинхронность совпадения связных между собой социально-экономических явлений. Временные лаги различаются на основе различных периодов, сдвигов во времени, изменяя показатели.
Различают лаги со сдвигом 1,2 и более периодов времени. Однако, при сдвиге лага более чем на 10 периодов времени, уже не имеет смысла применение методов анализа связных между собой социально-экономических явлений.
При наличии временного лага коэффициент корреляции рассчитывается при условии, что один их рядов исследуемого связного ряда динамики будет сдвинут на несколько периодов времени. Данный коэффициент корреляции определяется как:
, Vx – ряд фактического признака, Vy – ряд динамики результативного признака, сдвинутого на определенное количество лет во времени.
Следует отметить, что уравнение авторегрессии также строится при условии сдвига одного или нескольких показателей, связных между собой во времени. Однако, в этих случаях всегда принимается во внимание, что лаг является дискретной величиной. В то же время практика показывает, что временные лаги – это непрерывные величины.
содержание
|
|
|
