 |
Прогнозирование на основе кривых роста Гомперца и Перля-Рида.
|
|
|
|
Прогнозирование социально-экономических явлений на основе кривых роста (кривых насыщения) стало применяться сравнительно недавно. Впервые эти методы были использованы в начале ХХ века для прогнозирования роста биологических популяций. Однако кривые роста хорошо себя зарекомендовали и при прогнозировании социально-экономических явлений. Их применение в этом случае требует соблюдения определенных условий.
1. Исходный временной ряд должен быть достаточно длинным (30-40 лет).
2.Исходный временной ряд не должен иметь скачков, и тенденция такого ряда должна описываться достаточно плавной кривой.
3.Использование кривых роста в прогнозировании социально-экономических явлений может давать достаточно хорошие результаты, если предел насыщения будет определен сравнительно точно.
Кривые роста отражают кумулятивные возрастания к определенному заранее максимальному пределу. Особенностью кривых роста является то, что абсолютные приращения уменьшаются по мере приближения к пределу. Однако процесс роста идет до конца. Значение кривых роста как методов статистического прогнозирования социально-экономических явлений состоит в том, что они способствуют эмпирически правильному воспроизведению тенденции развития исследуемого явления. Наиболее распространенными кривыми роста, используемыми в статистической практике прогнозирования, являются кривая роста Гомперца и кривая роста Перля-Рида. Обе кривые, в общем, похожи одна на другую и графически изображаются S-образной кривой. Особенностью уравнений этих кривых является то, что их параметры могут быть определены методом наименьших квадратов лишь приближенно. Для расчета параметров этих кривых используется ряд искусственных методов, основанных на разбиении исходного ряда динамики на отдельные группы. Например, для того чтобы осуществить прогноз на основе кривой роста Гомперца необходимо выполнить следующее:
|
|
|
1. кривая описывается уравнением: 
2. прологарифмировав уравнение, получаем: 
,где: lg a — логарифм максимального значения, к которому приближается прогнозный уровень явления; lg b — расстояние, которое отделяет в каждый данный момент значение уровня от его максимального значения; с — имеет значение от нуля до единицы; х — начало на шкале х, к которому относится первое значение уровня (t = 0, 1, 2, …, n);
3. затем весь ряд динамики разбивается на три приблизительно равные части:
длины ряда;
4. для каждой выделенной части рассчитываются суммы логарифмов значений уровней 
;
5. затем определяются первые разности по этим суммам: 
6. на основании этих расчетов получим параметры уравнения с, 
которые рассчит. следующим образом: 
где:n — число уровней ряда в каждой части; 
, можно прогнозировать, если 
, 
Чтобы использовать данную кривую для экстраполяции за пределы исходного ряда динамики, достаточно подставить соответствующее значение 
в уравнение кривой. Наряду с кривой роста Гомперца достаточно широкое распространение получила кривая роста Перля-Рида, которая в прогнозировании социально-экономических явлений впервые была использована для демографических расчетов американским учеными – биологом Р. Перлем и математиком Л. Ридом.
Эта кривая выражает модифицированную геометрическую прогрессию, в которой возрастание затухает по мере приближения к некоторому определенному пределу. Максимальный предел устанавливается, прежде всего, на основании конкретного изучения исследуемого социально-экономического явления. Так же, как и кривая Гомперца, кривая Перля-Рида использует тот же искусственный прием для определения параметров кривой. Однако следует отметить, что по сравнению с кривой Гомперца прогнозные данные, полученные по этой кривой, имеют некоторую неопределенность. Кривая роста Перля-Рида описывается уравнением: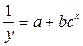 
|
|
|
Параметры уравнения находятся следующим образом: 
Из приведенных расчетов видно, что параметры уравнения кривой роста Перля-Рида определяются так же, как и параметры кривой роста Гомперца, за исключением того, что в последнем случае не используется прием логарифмирования. Кроме того, нужно иметь в виду, что в зависимости от масштаба данных величина 
умножается на 10000, 100000 или 1000000.
содержание
|
|
|
