Примеры. Самостоятельные упражнения. Тема 8. Интерполяция и аппроксимация функций в системе Maple

Примеры

1. Найти неопределенные интегралы (первообразные):

а) ;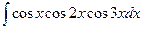

б) .

   > Int(cos(x)*cos(2*x)*cos(3*x), x)=int(cos(x)*cos(2*x)*cos(3*x), x);

  > Int((3*x^4+4)/(x^2*(x^2+1)^3), x)= int((3*x^4+4)/(x^2*(x^2+1)^3), x);

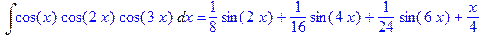
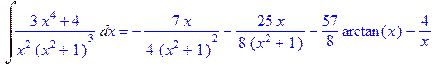
2. Найти определенный интеграл 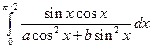 при условии, что параметры a> 0, b> 0.

> assume(a> 0); assume(b> 0);   Int(sin(x)*cos(x)/(a*cos(x)^2+b*sin(x)^2), x=0.. Pi/2)=  int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*sin(x)^2), x=0.. Pi/2);

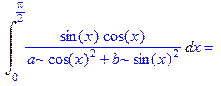
3. Найти несобственный интеграл 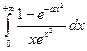 при условии, что параметр a> -1.

  > restart; assume(a> -1);     > Int((1-exp(-a*x^2))/(x*exp(x^2)), x=0.. +infinity)=       int((1-exp(-a*x^2))/(x*exp(x^2)), x=0.. +infinity);

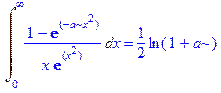
(Здесь нами использована команда restart для того, чтобы полностью очистить внутреннее ядро системы Maple от всех ранее уже использованных переменных и выражений и, тем самым, фактически начать работать заново)

4. Численно найти определенный интеграл .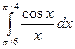

   > Int(cos(x)/x, x=Pi/6.. Pi/4)=evalf(int(cos(x)/x, x=Pi/6.. Pi/4), 15);

(В этом примере значение интеграла будет выведено на экран с 15 знаками после запятой)

5. Полностью проделать все этапы вычисления интеграла  по частям.

   > restart; J=Int(x^3*sin(x), x);

   > with(student): J=intparts(Int(x^3*sin(x), x), x^3);

  > intparts(%, x^2);

  > intparts(%, x);

  > value(%);

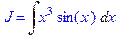
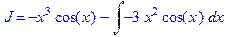
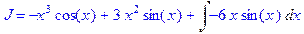
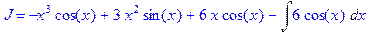
6. Вычислить интеграл 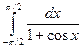 с помощью универсальной тригонометрической подстановки .

 > J=Int(1/(1+cos(x)), x=-Pi/2.. Pi/2);

  > J=changevar(tan(x/2)=t, Int(1/(1+cos(x)), x=-Pi/2.. Pi/2), t);

  > value(%);

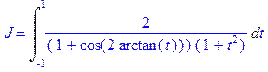
Самостоятельные упражнения

1. Вычислить неопределенный интеграл .

2. Вычислить несобственный интеграл 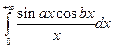 при a> 0, b> 0 для трех случаев: a> b; a=b; a< b.

3. Найти численно (т. е. приближенно) интеграл .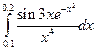

4. Полностью проделать все этапы вычисления определенного интеграла 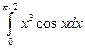, используя для этого формулу интегрирования по частям.

5. Найти значение интеграла , используя для этого универсальную тригонометрическую подстановку .

Тема 8. Интерполяция и аппроксимация функций в системе Maple

В системе Maple имеется несколько команд, реализующих обычную и сплайн-интерполяцию, а также метод наименьших квадратов для приближения экспериментальных данных.

В результате выполнения любой из этих команд формируется выражение, которое затем можно преобразовать в процедуру. Для оформления выражения в виде процедуры используется команда unhappy или команда из пакета codegen:

  > fproc: =codegen[makeproc](f, x);

Здесь fproc - имя формируемой процедуры, х - независимая переменная.

Для построения интерполяционного многочлена относительно переменной var по таблице, заданной векторами Х, Y используется команда interp(X, Y, var).

Массивы, задающие узлы интерполяции, могут быть не упорядочены, но массив Х не должен содержать одинаковых элементов. Векторы Х и Y должны содержать n+1 координат точек исходной зависимости, где n - степень интерполяционного полинома.

Покажем на примере технику применения полиномиальной аппроксимации на основе команды interp с построением аппроксимирующего полинома.

> X: =[0, 1, 2, 3, 4, 5]: Y: =[0, 1, 4, 3, 2, 1]: f: =interp(X, Y, x);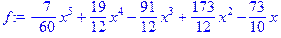

Построение сплайна по переменной var по табличным значениям, находящимся в массивах Х0, Y0, производится при помощи команды spline(X0, Y0, x, d). Отметим, что в массиве X0 хранящиеся значения должны быть отличны друг от друга и строго упорядочены по возрастанию. Длины этих массивов одинаковы и равны N.

Параметр d определяет порядок сплайна, который может быть линейным (linear), квадратичным (quadratic), кубическим (cubic) или четвертой степени (quartic). Порядок сплайна определяет степень полинома, которым приближается таблично заданная функция на каждом из подсегментов.

По умолчанию строится кубический сплайн. Результатом выполнения этой команды будет построение сплайна в виде гладкой функции (для всех случаев, кроме linear), задаваемой соответствующими формулами на каждом из подсегментов.

Результат вычисления сплайна будет представлен в виде следующей записи (формы):

piecewise(x< X0[2], P[1], x< X0[3], P[2],..., P[N]),

что эквивалентно следующей записи:

if x < X0[2] then (выражение P[1]) elif x < X0[3] then (выражение P[2])... else P[N] end if

Приведем пример построения сплайнов всех четырех видов:

> restart; X: =[0, 1, 2, 3, 4, 5]; Y: =[0, 1, 4, 3, 2. 5, 10];   f1: =spline(X, Y, x, linear); fc: =spline(X, Y, x, cubic);

> fq: =spline(X, Y, x, quadratic); fq1: =spline(X, Y, x, quartic);

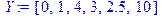
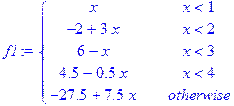
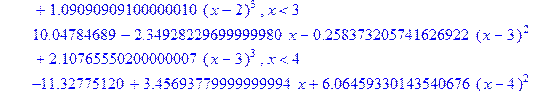
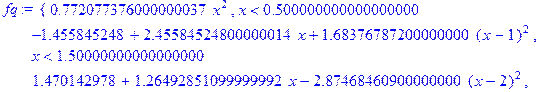
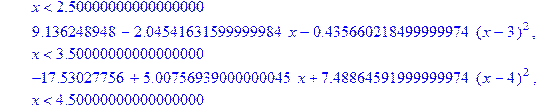
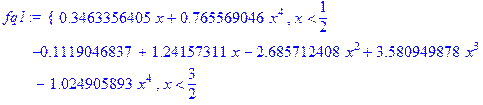
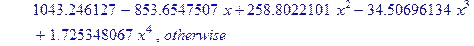
Построим теперь на одном рисунке графики всех четырех полученных сплайнов:

> plot([f1, fc, fq, fq1], x=-1.. 6, color=black);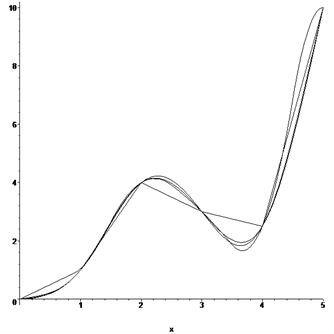

Рис. Графики вычисленных сплайнов (всего 4 кривые)

Далее преобразуем полученное выражение для наиболее употребляемого в практике кубического сплайна (fc) в отдельную процедуру с целью последующего использования в вычислениях:

> fqproc: =codegen[makeproc](fc, x);

> y_0: =fqproc(0); y_1: =fqproc(1); y_2: =fqproc(2);   y_3: =fqproc(3); y_4: =fqproc(4); y_5: =fqproc(5);

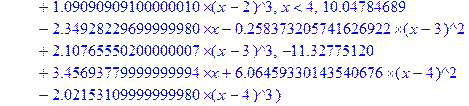
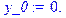
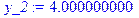
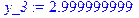
Другим хорошо известным способом приближения числовых данных является метод наименьших квадратов (англ. – least-squares). Результатом применения этого метода является функция заданного параметрического вида, наименее всего уклоняющаяся от заданных точек.

Для применения этого метода в системе Maple можно воспользоваться командами линейной алгебры или использовать команду leastsquare из пакета stats. Входными параметрами команды leastsquare являются имена переменных, вид функции и набор точек.

Построим методом наименьших квадратов приближение в виде кубического полинома тестового набора данных Х, Y, подключив предварительно пакет статистики stats:

> restart: with(stats): X: =[0, 1, 2, 3, 4, 5]; Y: =[0, 1, 4, 3, 2. 5, 10];   least_squares: =fit[leastsquare[[x, y], y=a*x^4+b*x^3+c*x^2+d*x+e]]([X, Y]);

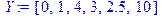
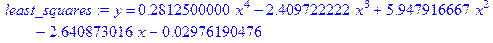
Как и ранее, преобразуем теперь полученное выражение в процедуру, при помощи которой возможно производить расчеты по полученной формуле:

> eq_least_squares: =unapply(rhs(least_squares), x);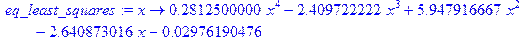

Далее построим график полученной функции (это полином четвертой степени по переменной x):

> plot([eq_least_squares(x), f1], x=-1.. 6, color=black, thickness=[4, 1]);

 

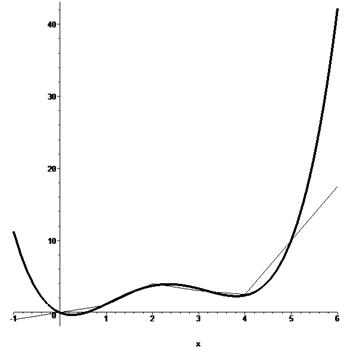
На этом рисунке кривая, нарисованная толстой линии, соответствует графику полинома четвертой степени, построенного по методу наименьших квадратов. Ломаная линия представляет собой ранее построенный линейный сплайн f1.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: