Порядок выполнения кластерного анализа.

1. Формулировка проблемы.

Самая важная часть формулирования проблемы кластеризации — это выбор пере­менных, на основе которых проводят кластеризацию. Включение даже одной или двух посторон­них (не имеющих отношение к группированию) переменных может исказить результаты класте­ризации. Задача состоит в том, чтобы выбранный набор переменных смог описать сходство между объектами с точки зрения признаков, имеющих отношение к данной проблеме маркетингового исследования. Переменные следует выбирать, исходя из опыта прошлых исследований, теории или тестируемой гипотезы. Экспериментатор должен обладать интуицией и уметь делать выводы.

2. Определение метода кластеризации.

Существует два подхода к формированию кластеров — иерархический и не­иерархический. Иерархическая кластеризация может использовать подход «сверху вниз» (все объекты помещаются в один кластер, после чего разделяют­ся — иногда до тех пор, пока каждый объект не окажется в своем «индивидуальном» кластере), или «снизу вверх» (каждый объект находится в своем собственном кла­стере, после чего начинается их объединение — иногда до тех пор, пока все объекты не окажутся в одном кластере). Если объект связан с другим объектом в своем кластере, они останутся вместе и далее.

Программа неиерархической кластеризации отличается лишь тем, что она по­зволяет объектам покидать один кластер и присоединяться к другому в процессе образования кластеров, если это улучшает значение критерия кластеризации. При использовании этого подхода сначала определяется центр кластера, после чего все объекты, которые попадают в заранее определенное пороговое расстояние от него, включаются в этот кластер. Если требуется получить решение с тремя кла­стерами, определяются три центра. Эти центры могут быть случайными числами, а могут быть получены в результате иерархической кластеризации.

Среди неиерархических методов (также известных как итеративное деление или методы k-средних ) тремя наиболее часто используемыми яв­ляются последовательный пороговый метод, параллельный пороговый метод и ме­тод оптимизации.

Последовательный пороговый метод. В данном случае выбирается центр кластера, и все объекты, попадающие в некото­рое заранее определенное пороговое значение, объединяются. Далее выбирается новый центр кластера, и процесс повторяется для не вошедших в кластеры объек­тов и т. д. После того как объект попадает в кластер, он не подлежит дальнейшей обработке.

Параллельный пороговый метод. Этот метод аналогичен предыдущему, за тем исключением, что одновременно вы­бираются несколько центров кластеров, и объекты, попадающие в пороговое зна­чение, относятся в кластер, центр которого является ближайшим по отношению к ним.

Метод оптимизации. Этот метод — модификация двух предыдущих, которая заключается в том, что объекты могут быть переведены из одного кластера в другой в ходе оптимизации по некоторому общему критерию, — такому, как среднее внутрикластерное рас­стояние для данного числа кластеров.

3. Выбор меры расстояния.

Чтобы группировать объекты, необходим некоторый показатель сходства или раз­личия. Схожие объекты группируются вместе, а те, что отстоят от них, попадают в другие кластеры. Среди наиболее часто используемых в кластерном анализе показателей можно перечислить следующие.

Евклидово расстояние. Евклидово расстояние между двумя точками х и у — это наименьшее расстояние между ними.

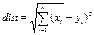
Квадрат евклидового расстояния. Благодаря возведению в квадрат при расчёте лучше учитываются большие разности. Эта мера должна всегда использоваться при построении кластеров при помощи центроидного метода и метода Варда.

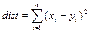
Расстояние городских кварталов – дисперсионная мера называемая дистанцией манхетенского таксиста. Определяется суммой абсолютных разностей по значению. Это и прямолин. Евклидово расстояние между 3-мя точками, а путь кот. Должен преодолеть таксист, чтобы проехать от одного дома к др. пересекается под прямым углом.

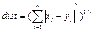
Мера хи-квадрат. Для того, чтобы найти расстояние между двумя наблюдениями, сравнивают частоты выпадения переменных, относящихся к этим наблюдениям. Квадратный корень из значения хи-квадрат будет применяться в качестве дистанционной меры.

Мера фи-квадрат. Эта мера представляет собой попытку нормализации меры хи-квадрат. Для этого она делится на квадратный корень общей суммы частот.

Существуют и другие меры расстояния. Выбор меры расстояния зависит от типа критериев кластеризации (например, для интервальных и относительных переменных целесообразно применять евклидово расстояние, квадрат евклидова расстояния, меру Чебышева и др.), их количества (например, при большом количестве критериев используют корреляцию Пирсона) и выбранного метода объединения (например, для центроидной и дисперсионной кластеризации целесообразно ее осуществление на основе квадрата евклидова расстояния).

4. Принятие решения о количестве кластеров.

Главный вопрос кластерного анализа — как определить соответствующее число кластеров. Существует несколько подходов.

Определение, основанное на предварительной информации. Аналитик может заранее определить это число, исходя из теоретических знаний и логики. Кроме того, у ана­литика могут быть некоторые практические соображения в пользу того или иного числа кластеров — в зависимости от того, как он собирается их использовать.

Определение, основанное на уровне кластеризации. Можно задать уровень кластеризации, который будет выра­жен значением ее критерия. Если критерий кластеризации может быть легко интер­претирован, как, например, средняя схожесть внутри кластеров, следует определить уровень, который и покажет число кластеров.

Определение числа кластеров на основании мо­дели кластеров, которую генерирует программа. В качестве полезного руковод­ства в иерархической кластеризации могут выступать расстояния между кластерами на последовательных шагах, и аналитик принимает решение остановиться, когда расстояние превысит опре­деленное значение или когда расстояние между кластерами после очередного шага скачкообразно изменится. Эти расстояния иногда называют показателями измен­чивости ошибки.

Определение числа кластеров на основе графика зависимости отношения дисперсий от числа кластеров. При неиерархической кластеризации можно построить график зависимости от числа кластеров отно­шения суммарной дисперсии внутри групп к межгрупповой дисперсии. Точка резкого перегиба кривой и показывает соответствующее число кластеров.

Определение числа кластеров, основанное на их размерах. Относительные размеры кластеров должны быть достаточно выразительными и соотносимыми.

5. Интерпретация и профилирование кластеров.

После формирования кластеров аналитику нужно их описать. Одним из часто используемых показателей является центроид — среднее значение объектов кла­стера по каждой из переменных, формирующих профиль каждого объекта.

Полезно профилировать кластеры в терминах переменных, которые не были использованы для кластеризации. Сюда могут входить демографические, психо­графические факторы, характеристики использования продукта и средств массо­вой информации и другие переменные.