Поверхности. Ориентация поверхностей

Поверхности определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:

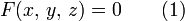
Если функция непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью.

Помимо указанного выше неявного способа задания поверхность может быть определена явно, если одну из переменных, например z, можно выразить через остальные:

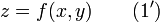
Также существует параметрический способ задания. В этом случае поверхность определяется системой уравнений:

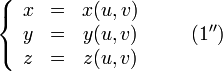
Пусть на плоскости с прямоугольной системой координат u и v задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам 0 < u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u', v') были различными соответствующие точки (x, у, z) и (x', у', z').Примером простой поверхности является полусфера.

Случай неявного задания. Поверхность, заданная уравнением 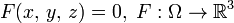, является гладкой регулярной поверхностью, если 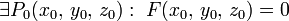, функция непрерывно дифференцируема в своей области определения 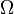, а её частные производные одновременно не обращаются в нуль (условие правильности) на всём множестве :

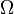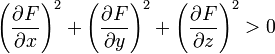
Случай параметрического задания. Зададим поверхность векторным уравнением 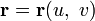, или, что то же самое, тремя уравнениями в координатах:

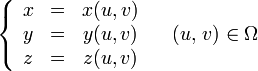
Эта система уравнений задаёт гладкую регулярную поверхность, если выполнены условия:

-система устанавливает взаимно однозначное соответствие между образом и прообразом ;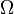

-функции 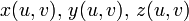непрерывно дифференцируемы в ;

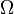-выполнено условие невырожденности: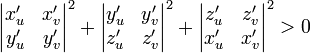

Геометрически последнее условие означает, что векторы 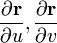нигде не параллельны.

Параметры u, v можно рассматривать как внутренние координаты точек поверхности. Фиксируя одну из координат, мы получаем два семейства координатных кривых, покрывающих поверхность координатной сеткой.

Случай явного задания. Поверхность может быть определена как график функции ; тогда является гладкой регулярной поверхностью, если функция дифференцируема. Этот вариант можно рассматривать как частный случай параметрического задания: .

Поверхность называется двусторонней, если при её обходе по замкнутому контуру из точки М, после возвращения в эту точку, вектор нормали в этой точке не поменял своего направления. Если же направление вектора изменится на 180^о,то такая поверхность называется односторонней. Примером двусторонней пов-ти могут служить: плоскость, коническая пов-ть и т.д.Примером односторонней пов-ти служит пов-ть Мебиуса.

Простейшим примером ориентируемой поверхности является плоскость xOy. Единичные векторы, перпендикулярные плоскости и идущие в положительном направлении оси z, определяют одну сторону плоскости, а векторы, идущие в отрицательном направлении оси z - другую сторону плоскости. Поверхность эллипсоида также ориентируема - выпущенный из какой-либо ее точки единичный вектор нормали во внешность эллипсоида, непрерывно продолжается на всю поверхность.

Этим поверхность ориентирована (определена внешняя сторона эллипсоида). Другая, противоположная, ориентация этой поверхности определяется единичным нормальным к ней вектором, идущим внутрь эллипсоида (внутренняя сторона эллипсоида).

Eсли есть гладкая поверхность S, определенная параметрическими уравнениями (1) с указанными там свойствами, то она ориентируема. Знаку «+» в формуле (3) соответствует определенная ориентация S, а знаку «-» будет тогда соответствовать противоположная ориентация. Cуществуют гладкие поверхности не ориентируемые, лист Мебиуса не ориентируем.