 |
Пови-2.Его определение и свой-ва
|
|
|
|
Рассмотрим двустороннюю поверхность  , гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
, гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
Для определенности предположим сначала, что поверхность задана явным уравнением  причем точка
причем точка  изменяется в области
изменяется в области  на плоскости (х,у), ограниченный кусочно-гладким контуром.
на плоскости (х,у), ограниченный кусочно-гладким контуром.
Пусть теперь в точках данной поверхности  определена некоторая функция
определена некоторая функция 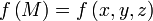 . Разбив поверхность сетью кусочно-гладких кривых на части
. Разбив поверхность сетью кусочно-гладких кривых на части  и выбрав на каждой такой части точку
и выбрав на каждой такой части точку  вычисляем значение функции
вычисляем значение функции  в данной точке и умножим его на площадь
в данной точке и умножим его на площадь  проекции на плоскость (х,у) элемента
проекции на плоскость (х,у) элемента  , снабженную определенным знаком. Составим интегральную сумму:
, снабженную определенным знаком. Составим интегральную сумму:
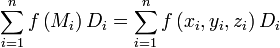
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от 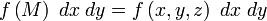
Свойства Пови-2:
1)свой-во линейности: 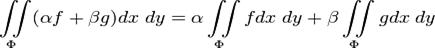
2)свой-во аддитивности: 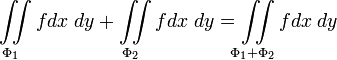
3) При изменении ориентации поверхности, поверхностный интеграл меняет знак/
Вычисление Пови-2
Пови-2 по разным сторонам  и
и  одной и той же пов-ти S вычисляется:
одной и той же пов-ти S вычисляется:

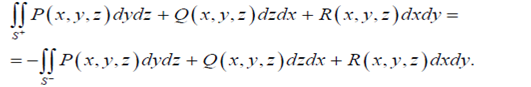
Для Пови-2 существует несколько способов вычисления:
I)Переход от Пови-2 к Пови-1

II) Непосредственный переход к двойному интегралу. 

Векторное поле. Векторные линии поля
 , Это выражение называют векторным дифференциальным оператором или оператором Гамильтона.
, Это выражение называют векторным дифференциальным оператором или оператором Гамильтона.
Если каждой точке М данной области Е соответствует определенный вектор 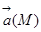 , то говорят, что в области Е задано векторное поле. В декартовой системе координат векторное поле
, то говорят, что в области Е задано векторное поле. В декартовой системе координат векторное поле 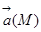 задается тремя функциями P,Q,R, определенными в области Е
задается тремя функциями P,Q,R, определенными в области Е
 .
.
Здесь и в дальнейшем будем предполагать, что эти функции во всей области непрерывны вместе с частными производными. Для плоского векторного поля:
|
|
|
 .
.
Векторной линией данного поля 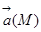 называют такую линию ℓ, в каждой точке которой вектор
называют такую линию ℓ, в каждой точке которой вектор 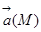 имеет направление касательной к этой линии. Через каждую точку векторного поля проходит (при условии, что
имеет направление касательной к этой линии. Через каждую точку векторного поля проходит (при условии, что  )одна векторная линия. Совокупность всех векторных линий определяется системой дифференциальных уравнений:
)одна векторная линия. Совокупность всех векторных линий определяется системой дифференциальных уравнений:
 .
.
Векторные линии характеризуют векторные поля геометрически и дают известную информацию о структуре этого поля. В векторном поле  векторные линии нормальны в каждой точке поверхностям уровня F(x,y,z) = С; вдоль этих линий функция F(M) изменяется быстрее всего. В случае плоского векторного поля векторные линии определяется уравнением:
векторные линии нормальны в каждой точке поверхностям уровня F(x,y,z) = С; вдоль этих линий функция F(M) изменяется быстрее всего. В случае плоского векторного поля векторные линии определяется уравнением: 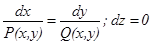
Поток векторного поля
Поток векторного поля 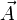 — однопараметрическое семейство диффеоморфизмов
— однопараметрическое семейство диффеоморфизмов  , определяемых дифференциальным уравнением:
, определяемых дифференциальным уравнением: 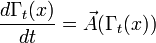
Поток векторного поля через поверхность — поверхностный интеграл первого рода по поверхности  . По определению:
. По определению: 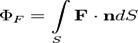
Где  — векторное поле (вектор-функция векторного аргумента — точки пространства),
— векторное поле (вектор-функция векторного аргумента — точки пространства),  — единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — то есть для дифференцируемой поверхности — так, чтобы
— единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — то есть для дифференцируемой поверхности — так, чтобы  было непрерывно; для не ориентируемой поверхности это не важно, так как поток через неё всегда ноль),
было непрерывно; для не ориентируемой поверхности это не важно, так как поток через неё всегда ноль),  — элемент поверхности.
— элемент поверхности.
В трёхмерном случае  , а поверхностью является обычная двумерная поверхность.
, а поверхностью является обычная двумерная поверхность.
Иногда, особенно в физике, применяется обозначение: 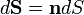 ;тогда поток записывается в виде:
;тогда поток записывается в виде: 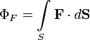
Физическая интерпретация: Пусть движение несжимаемой жидкости единичной плотности в пространстве задано векторным полем скорости течения  . Тогда объем жидкости, который протечёт за единицу времени через поверхность
. Тогда объем жидкости, который протечёт за единицу времени через поверхность  , будет равен потоку векторного поля
, будет равен потоку векторного поля 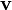 через поверхность
через поверхность  .
.
|
|
|
|
|
|


