 |
Расчёт зубчатых колес редуктора
|
|
|
|
Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками: для шестерни сталь 45, термическая обработка – улучшение, твёрдость НВ 230; для колеса – сталь 45, термическая обработка – улучшение, но твердость на 30 единиц ниже - НВ 200. Разница твердости объясняется необходимостью равномерного износа зубьев зубчатых колес.
Определим допускаемое контактное напряжение:
, (11)
где σHlimb – предел контактной выносливости при базовом числе циклов,
σHlimb=2 HB+70, [1, с. 34, табл. 3.2];
KHL – коэффициент долговечности, KHL=1, [1, с. 33];
[SH] – коэффициент безопасности, [SH] =1.1, [1, с. 33].
Для шестерни
, (12)
482 МПа.
Для колеса
, (13)
=428 МПа.
Для непрямозубых колёс расчётное допускаемое контактное напряжение определяется по формуле
, (14)
[σH]=0,45·([482 +428]) = 410 МПа.
Требуемое условие 
выполнено.
(Для прямозубых передач [σH]= [σH2])
Определяем межосевое расстояние.
Межосевое расстояние из условия контактной выносливости определяется по формуле
, (15)
где Ka– коэффициент для косозубой передачи, Ka=43, [1, с. 32], (Для прямозубых Ka=49,5);
U1 – передаточное число редуктора, U1=3,15, (ПЗ, задание);
М2– вращающий момент на ведомом валу, М2=156,2 Н·м, (ПЗ, табл.1);
КНВ – коэффициент, учитывающий неравномерность распределения
нагрузки, КНВ=1, [1, с.32];
[σH] – допускаемое контактное напряжение, [σH]=410MПа;
ψba – коэффициент ширины венца, ψba=0,4, (ПЗ, задание).
аω= 43·(3,15+1)· 
=110 мм.
В первом ряду значений межосевых расстояний по ГОСТ 2185-66 выбираем ближайшее и принимаем аω=125 мм, [1, с. 36].
Определяем модуль передачи
Нормальный модуль зацепления принимают по следующей рекомендации:
мм.
Принимаем по ГОСТ 9563-60, 
=2 мм, [1, с. 36]. (В силовых передачах ≥1,5 мм.)
|
|
|
Определяем угол наклона зубьев и суммарное число зубьев
Принимаем предварительно угол наклона зубьев β=9º, (ПЗ, задание) и определяем суммарное число зубьев
, (16)
где 
– межосевое расстояние, =125 мм;
– нормальный модуль зацепления, =2 мм.
Z∑ = 
=123,39.
Принимаем Z∑=123.
Определяем числа зубьев шестерни и колеса.
Число зубьев шестерни равно:
, (17)
где U1 – передаточное число редуктора, U1=3,15;
Z∑= 123 – суммарное число зубьев, Z∑= 123.
= 
=29,64.
Принимаем =30.
Определяем число зубьев колеса:
Z2= Z∑ -Z1, (18)
Z2=123-30=93.
Уточняем передаточное число
(19)
где Z1 – число зубьев шестерни, Z1=30;
Z2 – число зубьев колеса, Z2=93.
U1ф= 
3,1.
Уточняем угол наклона зубьев:
, (20)
где mn– модуль передачи, mn=2 мм;
аω – межосевое расстояние, аω=125 мм.
cos β = 
=0,984.
Принимаем 
β=10º26'.
Определяем диаметры колес и их ширину.
Делительный диаметр шестерни:
, (21)
где mn – модуль передачи, mn=2 мм;
Z1– число зубьев шестерни, Z1=30;
– косинус угла наклона зубьев, =0,984.
d1= 
60,98 мм
Делительный диаметр колеса:
, (22)
где Z2– число зубьев колеса, Z2= 93.
d2= 
=189,02 мм
Проверяем межосевое расстояние:
aw= 
мм
Определим диаметры вершин зубьев:
, (23)
da1=60,98 +2·2=64,98 мм;
da2=189,02 +2·2=193,02 мм.
Определим диаметры впадин зубьев:
df1 = d1 -2,5 mn.
df1 =60,98-2,5·2=55,98 мм;
df2=189,02-2,5·2=184,02 мм.
Определяем ширину колеса:
, (24)
где 
– коэффициент ширины венца, =0,4;
аω– межосевое расстояние, аω=125 мм.
b2=0,4·125=50 мм.
Определяем ширину шестерни:
, (25)
b1=50+5=55 мм.
Определяем коэффициент ширины шестерни по диаметру:
, (26)
ψba= 
.
Определяем окружные скорости и значения степени точности изготовления шестерни и колеса.
υ= 
, (27)
где n1– частота вращения шестерни,
n1=967 об/мин, (ПЗ, п.1);
d1 – делительный диаметр шестерни, d1=60,98 мм.
υ = 
=3,09 м/с.
При такой скорости для косозубых колес принимаем 8-ю степень точности, [1, с. 32].
Определяем коэффициент нагрузки, проверяем зубья на контактное напряжение
|
|
|
, (28)
где KHB – коэффициент, учитывающий неравномерность
распределения нагрузки по ширине венца, KHB=1,[1, табл. 3.5];
KHα- коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями, KHα=1,12, [1, табл. 3.5];
KHV – динамический коэффициент, KHV=1,1, [1, табл. 3.6].
Кн=1·1,12·1,1=1,23.
Проверяем зубья на контактные напряжения:
(29)
где aω – межосевое расстояние, aω=125 мм;
M2 – передаваемый момент, M2=156,2 Н·м, (ПЗ, п.1);
b2 -ширина колеса, b2=50 мм;
U1 – передаточное число редуктора, U1=3,1;
270-коэффициент для непрямозубых колес (для прямозубых зубчатых передач 310)
σH= 
=352,81МПа< 
=410 МПа.
< .
Определяем силы, действующие в зацеплении.
Определяем окружную силу:
Ft= 
, (30)
где M1– вращающий момент на валу шестерни, M1= 52,2 H·м;
d1– делительный диаметр шестерни, d1=60,98 мм.
Ft= 
= 1712 Н
Определяем радиальную силу:
, (31)
где 
- угол зацепления в нормальном сечении, = 20°, [1, с. 29];
- угол наклона зубьев, = 10° 26´.
Fr= 
=633 Н
Определяем осевую силу:
, (32)
Fa=1712·tg10º26´=295 Н.
(Для прямозубых и шевронных передач Fa=0)
Полученные данные приведем в таблице.
Таблица 2
| Наименование параметров и единица измерения | Обозначение параметров и числовое значение |
| Материал, вид термической обработки, твердость: шестерни колеса Допускаемое контактное напряжение, МПа: шестерни колеса Расчетное допускаемое контактное напряжение, МПа Межосевое расстояние, мм Нормальный модуль зацепления, мм Суммарное число зубьев Число зубьев: шестерни колеса Угол наклона зубьев Передаточное число редуктора Делительный диаметр, мм: шестерни колеса Диаметр вершин зубьев, мм шестерни колеса Диаметр впадин зубьев, мм шестерни колеса | |
Продолжение таблицы 2
| Наименование параметров и единица измерения | Обозначение параметров и числовое значение |
| Ширина, мм шестерни колеса Коэффициент ширины шестерни по диаметру Окружная скорость, м/c Степень точности изготовления Коэффициент нагрузки Окружная сила, Н Радиальная сила, Н Осевая сила, Н | b1=55 b2=50 ψba=1,23 υ=3,09 8 KH=1,123 Ft=1712 Fr=633 Fa=295 |
Методические указания
Разница твердости зубьев шестерен и колеса для прямозубых передач 25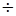 
30 HB, для косозубых передач и шевронных 30 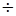50 HB.
|
|
|
Фактическое передаточное число должно отличаться от заданного не более чем на 3%.
Значения межосевого расстояния и нормального модуля рекомендуется выбирать из первого ряда. Угол наклона зубьев рассчитать с точностью до одной минуты, а для этого cosβ рассчитать до пятого знака после запятой.
Диаметры шестерни и колеса рассчитать с точностью до сотых долей мм. Ширину зубчатых колес округлить до целого числа. Окружная скорость для прямозубой передачи должна быть не более 5м/с. Контактные напряжения, возникающие в зацеплении должны быть в пределе до 5% -перегрузка и до 20% недогрузка.
|
|
|
