 |
Глава 1. Целочисленные функции (теоретические факты)
|
|
|
|
Федеральное агентство по образованию
Государственное общеобразовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
«Целочисленные функции»
Выполнила: студентка
V курса математического факультета Мошкина Т.Л.
Научный руководитель: старший преподаватель Семёнов А.Н.
 |
Рецензент:
|
Допущена к защите в ГАК
Зав. кафедрой Вечтомов Е.М.
«»
Декан факультета Варанкина В.И.
«»
|
Киров
2005
Содержание
Введение. 3
Глава 1. Целочисленные функции (теоретические факты) 4
I. Определения. 4
II. Связь с непрерывными функциями. 5
III. Количество целых чисел в интервалах: [ a, b ], [ a, b), (a, b), (a, b ] 7
IV. Спектры. 8
V. ‘Mod’: бинарная операция. 9
Глава 2. Целочисленные функции (применение к решению задач) 11
Литература. 28
Введение
Целые числа составляют костяк дискретной математики, и на практике часто приходится округлять дробные или произвольные вещественные числа до целых.
До недавнего времени для обозначения целой части вещественного числа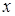 
использовалась запись 
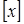. Но в начале 60-х годов Кеннет Э.Айверсон предложил в этом случае писать 
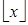и дал удачное название этому обозначению: «пол». Для обозначения верхнего целого он предложил запись 
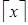и назвал её «потолком», а для квадратных скобок нашёл новое применение. Предложенная Айверсоном нотация оказалась настолько удачной, что за рубежом старое обозначение уже практически не встречается. С появлением русского издания книги Р.Грэхем, Д.Кнут, О.Паташник «Конкретная математика» эта нотация становится популярной и в России.
|
|
|
Цель данной работы — получить представление и навыки в обращении с «полом» и «потолком».
Задачи работы:
1. Осветить теоретические аспекты данной темы:
· Дать определение функций «пол», «потолок»;
· Рассмотреть некоторые свойства этих функций;
· Установить связь с непрерывными функциями;
· Подсчитать количество целых чисел в заданных интервалах;
· Рассмотреть определение спектра и его свойства;
· Дать определение бинарной операции «mod» и рассмотреть приложение этой операции;
· Рассмотреть на примере, как можно вычислить сумму, содержащую «полы».
2. Показать, как теория применяется на практике при решении задач.
Глава 1. Целочисленные функции (теоретические факты)
I. Определения.
Договоримся через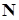 
обозначать множество всех натуральных чисел, т.е. множество всех целых положительных чисел. Определим для любого вещественного числа x функции наибольшего и наименьшего целого:
ë x û — наибольшее целое, меньше или равное x;
é x ù — наименьшее целое, больше или равное x.
Из определения ясно, что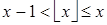 
, 
. Отсюда следует, что
(1)
В целых точках неубывающие функци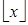и и 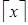совпадают, т.е. 
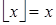Û 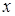— целое Û 
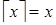. А если они не совпадают, то они отличаются на 1, т.е.
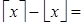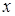[ - не целое] (2)
Эта формула связывает все три обозначения Айверсона. Здесь и далее квадратные скобки используются для произвольного высказывания P в таком смысле:
Функци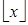и и 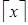являются отображениями друг друга относительно координатных осей, т.е.
, 
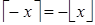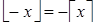(3)
Из определений «пола» и «потолка» легко следуют свойства этих функций: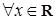 
и 
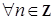
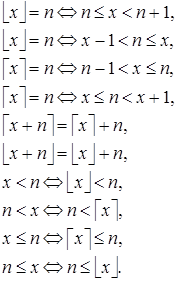(4)
|
|
|
Разность между 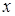и 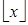называется дробной частью x и обозначается
Иногда 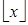называется целой частью 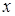, поскольку 
.
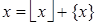Докажем следующее свойство рассматриваемых функций:
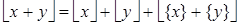(5)
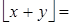
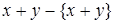
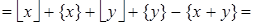
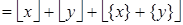
Так как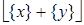 
равно либо 0, либо 1, то 
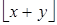равно либо 
, либо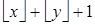 
.
II. Связь с непрерывными функциями.
Пусть 
— некоторая непрерывная монотонно возрастающая функция, обладающая тем свойством, что — целое число Þ 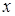— целое число. Тогда
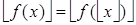(6)
и
(7)
всякий раз, когда определены функции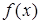 
, 
, 
.
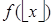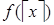Докажем, что
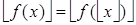
Случай 1: если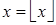 
, тогда 
.
Случай 2: если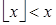 
, тогда 
(в силу того, что функция 
монотонно возрастающая), а так как функция «пол» — не убывающая, то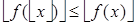 
. Предположим, что 
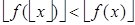, тогда существует такое число 
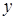, что 
и 
(в силу непрерывности функции ). Из условия следует, что 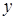— целое число. Это противоречит тому, что между 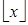и 
нет целых чисел. Значит,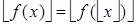 
.
Докажем, что
Случай 1: если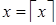 
, то 
.
Случай 2: если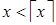 
, то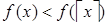 
(в силу того, что функция монотонно возрастающая), а так как функция «потолок» — не убывающая, то 
. Предположим, что 
, тогда существует такое число 
, что 
и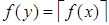 
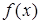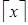(в силу непрерывности функции ). Из условия следует, что — целое число. Это противоречит тому, что между и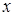 
нет целых чисел. Значит, 
.
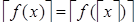Рассмотрев 
, получаем полезное свойство:
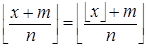и 
(8)
Например, при 
и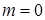 
получаем 
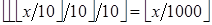, т.е. троекратное деление на 10 с последовательным отбрасыванием цифр остатка — это то же самое, что и непосредственное деление на 1000 с последующим отбрасыванием всего остатка.
III. Количество целых чисел в интервалах: [a, b], [a, b), (a,b), (a, b].
Будем рассматривать указанные интервалы при условии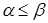 
.
Если a и b — целые числа, тогда интервал [ a, b) содержит ровно 
целых чисел: a, a +1, …,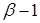 
, аналогично интервал (a, b ] содержит целых чисел, но a и b — произвольные вещественные числа. Из (4) следует
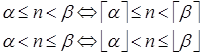, когда 
— целое число
Поэтому интервал [ a, b) содержит ровно 
целых чисел, а интервал (a, b ] содержит ровно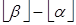 
целых чисел.
Рассмотрим промежуток [ a, b ]. Имеем 
(на основании свойств (4)). Отсюда следует, что рассматриваемый промежуток содержит ровно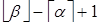 
целых чисел: 
, 
, …, 
, 
.
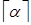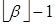Рассмотрим (a, b), причём 
. Имеем 
. Отсюда следует, что рассматриваемый интервал содержит ровно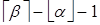 
целых чисел: 
, 
, …, 
, 
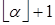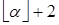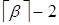. Если не вводить дополнительное ограничение 
то получим, что пустой интервал (a, a) содержит ровно 
целых чисел.
|
|
|
Подытожим установленные факты:
| Интервал | Количество целых чисел | Ограничение |
| [ a, b ] | ë b û - é a ù + 1 | a £ b |
| [ a, b) | é b ù - é a ù | a £ b |
| (a, b ] | ë b û - ë a û | a £ b |
| (a, b) | é b ù - ë a û -1 | a < b |
(9)
IV. Спектры.
Спектр некоторого вещественного числа a определяется как бесконечное мультимножество целых чисел:
Spec (a) = {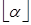 
, 
, 
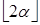,…} (10)
Если , то Spec (a)¹Spec (b), т.е. нет двух одинаковых спектров.
Действительно, если предположить, что 
, то найдётся некоторое положительное целое число 
, такое, что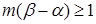 
. Следовательно, 
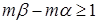и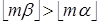 
. Таким образом, Spec(b) содержит менее чем m элементов не больших 
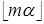, тогда как Spec(α) содержит по меньшей мере m.
Пусть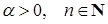 
. Число элементов в Spec(
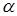), которые не превосходят 
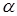, равно
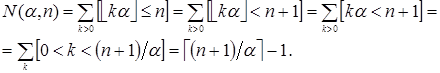(11)
Говорят, что спектры образуют разбиение всех целых положительных чисел, если любое число, отсутствующее в одном спектре, присутствует в другом; но никакое число не содержится одновременно в обоих. Пусть 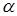и 
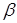— вещественные положительные числа, тогда Spec(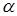) и Spec(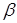) образуют разбиение натуральных чисел тогда и только тогда, когда 
. Интересное свойство спектров будет доказано в задаче 10. В задаче 17 будет показана связь между мультимножествами Spec(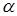) и Spec 
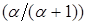, где 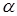— некоторое положительное число.
V. ‘Mod’: бинарная операция.
Если m и n — целые положительные числа, то неполное частное от деления n на m равно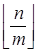 
. Для того, чтобы было удобно работать с остатками, введём определение остатка:
.
Это определение можно распространить на произвольные вещественные числа:
(12)
при 
. Положим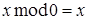 
.
Дробную часть числа x можно представить как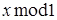 
.
Самым важным алгебраическим свойством операции ‘mod’ является распределительный закон:
(13)
Доказательство следует из (11):
.
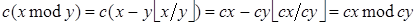Приложение операции ‘ mod ’: разложение n предметов на m групп как можно более равномерных. Решение этого вопроса даёт тождества, справедливые при целых 
и натуральных 
.
|
|
|
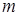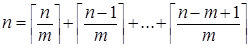— выражает разбиение n на m как можно более равных частей в невозрастающем порядке. (14)
— выражает разбиение n на m как можно более равных частей в неубывающем порядке. (15)
Доказательство этих фактов можно найти в книге Р.Грэхем, Д.Кнут, О.Паташник «Конкретная математика» на с.106-108. Если в (15) заменить n на ë mx ûи применить правило (8), то получим тождество, которое справедливо при любом вещественном x и натуральном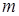 
:
(16)
|
|
|
12 |
