 |
Глава 2. Целочисленные функции (применение к решению задач)
|
|
|
|
Задача 1.
Всякое натуральное число представимо в виде: 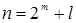 , где
, где 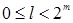 . Приведите явные формулы для l и m как функций от n.
. Приведите явные формулы для l и m как функций от n.
Решение:
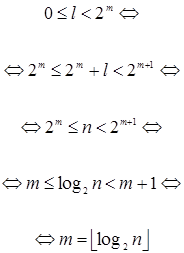

Тогда 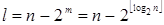
Ответ:  ,
, 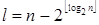 .
.
Задача 2.
Как выглядит формула для ближайшего целого к заданному вещественному числу x? В случае «равновесия» — когда x лежит ровно посередине между целыми числами — приведите выражение, округляющее результат:
a) в сторону увеличения, т.е. до é x ù;
b) в сторону уменьшения, т.е. до ë x û.
Решение:
Пусть вещественное число 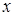 округляется до
округляется до 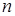 .
.
a) В этом случае до 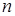 округляются числа
округляются числа 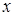 , удовлетворяющие неравенству:
, удовлетворяющие неравенству:
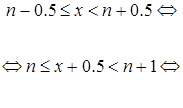
Û 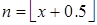 (по свойству (4)).
(по свойству (4)).
b) В этом случае до 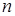 округляются числа
округляются числа 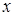 , удовлетворяющие неравенству:
, удовлетворяющие неравенству:
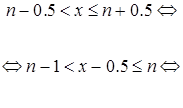
Û 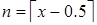 (по свойству (4)).
(по свойству (4)).
Ответ: a) 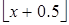 ; b)
; b) 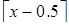
Задача 3.
Вычислите 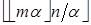 , если m и n — натуральные числа, а
, если m и n — натуральные числа, а 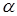 — иррациональное число, большее n.
— иррациональное число, большее n.
Решение:
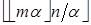 =
= 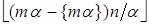 =
= 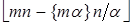 =
= 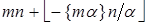 = =
= = 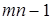 (так как
(так как 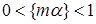 и
и 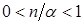 ).
).
Ответ: 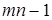 .
.
Задача 4.
Докажите, что 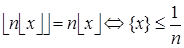 .
.
Доказательство:
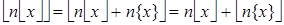 .
.
Отсюда 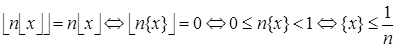 , так как n — натуральное число.
, так как n — натуральное число.
Итак, 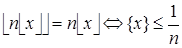 . Что и требовалось доказать.
. Что и требовалось доказать.
Задача 5.
Доказать, что если f (x) — непрерывная, монотонно убывающая функция и f (x) — целое Þ x — целое, тогда 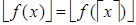 .
.
Доказательство:
1 случай: если 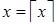 , то
, то 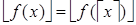 .
.
2 случай: если 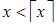 , то
, то 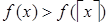 , так как f – убывающая функция;
, так как f – убывающая функция; 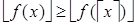 (в силу того, что функция «пол» — неубывающая).
(в силу того, что функция «пол» — неубывающая).
Если 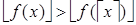 , то существует такое число
, то существует такое число 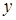 , что
, что 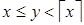 и
и 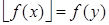 (так как f непрерывна). Поскольку f (y) целое, то по условию
(так как f непрерывна). Поскольку f (y) целое, то по условию 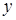 целое. А это противоречит тому, что между x и é x ù не может быть никакого целого числа. Следовательно,
целое. А это противоречит тому, что между x и é x ù не может быть никакого целого числа. Следовательно, 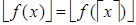 .
.
Что и требовалось доказать.
Задача 6.
Решите рекуррентность при целом 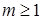
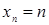 при
при 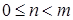 ,
,
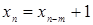 при
при 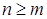 .
.
Решение:
Покажем, что 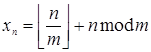 методом математической индукции по
методом математической индукции по 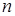 .
.
База: 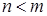 : из того, что
: из того, что 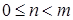 , следует, что
, следует, что 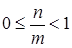 , тогда
, тогда 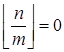 и
и 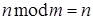 , поэтому для
, поэтому для 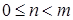 выполняется
выполняется 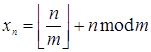 .
.
|
|
|
Переход: пусть для некоторого номера 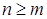 и для меньших номеров утверждение верно:
и для меньших номеров утверждение верно: 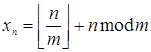 .
.
Докажем, что  .
.
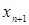 =
= 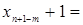
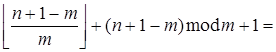
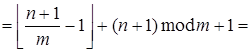
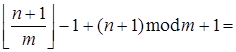
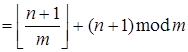 .
.
Что и требовалось доказать.
Задача 7.
Докажите принцип ящиков Дирихле: если n предметов размещены по m ящикам, то некоторый ящик должен содержать не меньше чем é n / m ù предметов, а некоторый ящик должен содержать не более чем ë n / m û.
Решение:
Предположим, что каждый ящик содержит меньше, чем é n / m ù предметов. Тогда наибольшее количество предметов в каждом ящике — это 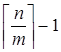 предметов. Следовательно, наибольшее количество предметов, размещённых по ящикам — это
предметов. Следовательно, наибольшее количество предметов, размещённых по ящикам — это 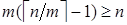 Þ
Þ 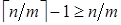 Þ
Þ 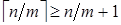 . Это противоречит тому, что
. Это противоречит тому, что 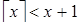 .
.
Значит, существует ящик, который содержит не менее чем é n / m ù предметов.
Предположим, что нет ящика, в котором не более, чем ë n / m û предметов, т.е. каждый ящик содержит более чем ë n / m û предметов. Тогда наименьшее количество предметов в каждом ящике — 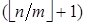 . Следовательно, наименьшее количество предметов, размещённых по ящикам — это
. Следовательно, наименьшее количество предметов, размещённых по ящикам — это 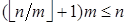 Þ
Þ 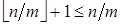 Þ
Þ 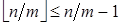 . Это противоречит тому, что
. Это противоречит тому, что 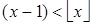 .
.
Значит, существует ящик, который содержит не более чем ë n / m û предметов.
Что и требовалось доказать.
Задача 8.
Покажите, что выражение 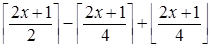 всегда равно либо ë x û, либо é x ù. При каких условиях получается тот или иной случай?
всегда равно либо ë x û, либо é x ù. При каких условиях получается тот или иной случай?
Решение:
1 случай: x = (4 k -1)/2, k ÎZ
Тогда 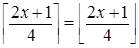 , так как
, так как 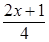 - целое число.
- целое число.
Получим 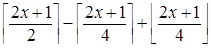 =
= 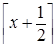 =
= 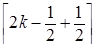 =
= 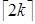 =
= 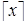
2 случай: x ¹ (4 k -1)/2, k Î Z, тогда 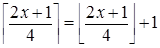 .
.
Получим 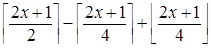 =
= 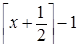 =
= 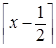
Итак, данное выражение округляет числа до ближайшего целого; в случае «равновесия» — когда x лежит ровно посередине между целыми числами — данное выражение округляет число в сторону чётного.
Задача 9.
Докажите, что  при любом целом n и любом целом положительном m.
при любом целом n и любом целом положительном m.
Доказательство:
Пусть 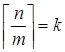 .
.
Покажем, что 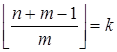 .
.
Имеем 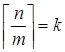 Û
Û
Û 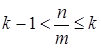 (по свойствам (4)) Û
(по свойствам (4)) Û
Û 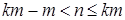 Û
Û
Û 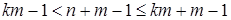 Û
Û
Û 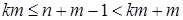 Û
Û
Û 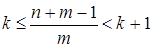 Û
Û
Û 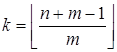
Что и требовалось доказать.
|
|
|
Задача 10.
Пусть α и β — вещественные положительные числа. Докажите, что Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел тогда и только тогда, когда α и β иррациональны и 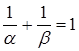 .
.
Решение:
Пусть α и β — вещественные положительные числа.
Докажем, что если Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел, то α и β — иррациональные числа и 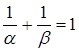 .
.
Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел, тогда 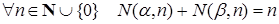 .
.
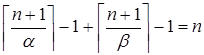 Þ
Þ
Þ 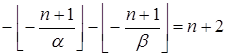 Þ
Þ
Þ 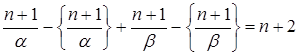 Þ
Þ
Þ  Þ
Þ
Þ 
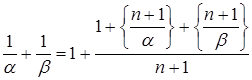
Рассмотрим 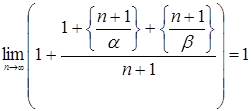 Þ
Þ
Þ 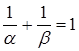 .
.
Докажем, что α и β иррациональны. Так как 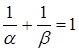 , то числа α и β либо оба рациональны, либо оба иррациональны.
, то числа α и β либо оба рациональны, либо оба иррациональны.
Если α и β оба рациональны, т.е. существует такое целое число m, что 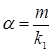 и
и 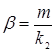 , где
, где 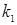 и
и 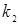 — натуральные числа, тогда
— натуральные числа, тогда 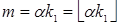 ÎSpec(α) и
ÎSpec(α) и 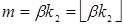 ÎSpec(β).
ÎSpec(β).
Но никакое число не содержится одновременно в двух спектрах, образующих разбиение всех целых положительных чисел. Следовательно, α и β — иррациональны.
Докажем обратное: если α и β иррациональны и 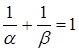 , то Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел.
, то Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел.
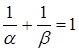 Þ
Þ 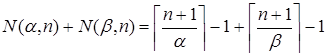
Так как 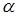 и
и  — иррациональны, то
— иррациональны, то 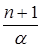 и
и 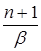 — не целые числа, то
— не целые числа, то
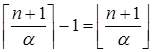
и

Отсюда получаем:
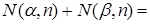
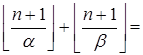
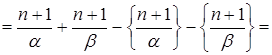
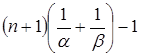 (так как
(так как 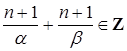 и
и 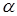 и
и 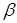 — иррациональны, то
— иррациональны, то 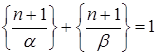 ).
).
Получаем, что 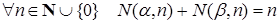 . Отсюда Spec(α) и Spec(β) образуют разбиение всех натуральных чисел.
. Отсюда Spec(α) и Spec(β) образуют разбиение всех натуральных чисел.
Что и требовалось доказать.
Задача 11.
Докажите, что  при целом n.
при целом n.
Доказательство:
· если 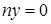 (
(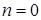 или
или 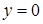 ), то
), то 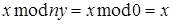 ,
,
тогда 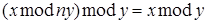 .
.
Получаем верное равенство 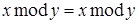 .
.
· если 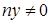 , тогда
, тогда 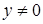 .
.
Правая часть имеет вид: 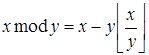 .
.
Преобразуем левую часть:
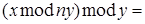
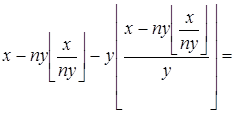
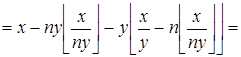
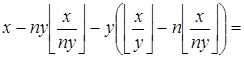
 .
.
Получили, что 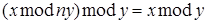 при любом целом
при любом целом 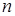 . Что и требовалось доказать.
. Что и требовалось доказать.
Задача 12.
Имеется ли аналогичное (16) тождество, в котором вместо «полов» используются «потолки»?
Решение:
Тождество (16) 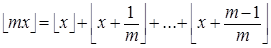 получается из тождества (15)
получается из тождества (15) 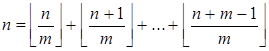 заменой n на ë mx û.
заменой n на ë mx û.
Аналогичное тождество для потолков получается из тождества (14) 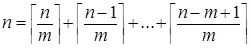 заменой n на é mx ù:
заменой n на é mx ù:
é mx ù = 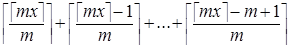 =
=
= 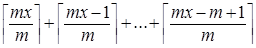 =
= 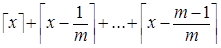
Итак, получили тождество аналогичное данному:
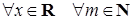 é mx ù =
é mx ù =  .
.
Задача 13.
Докажите, что 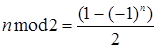 . Найдите и докажите аналогичное выражение для
. Найдите и докажите аналогичное выражение для  вида
вида 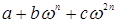 , где ω – комплексное число
, где ω – комплексное число  .
.
Доказательство:
При делении числа на 2 возможны только два различных остатка: либо 0, либо 1.
|
|
|
· если 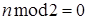 , то
, то 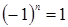 и
и 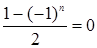 .
.
· если 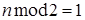 ,
, 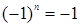 и
и 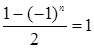 .
.
Следовательно, равенство 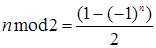 верно для любого натурального n. Что и требовалось доказать.
верно для любого натурального n. Что и требовалось доказать.
Найдём аналогичное выражение для 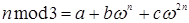 , т.е. найдём коэффициенты a, b, c.
, т.е. найдём коэффициенты a, b, c.
Поскольку 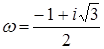 — есть корень третьей степени из 1, то
— есть корень третьей степени из 1, то 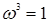 и
и 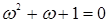 .
.
Так как 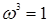 , то
, то 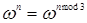 .
.
При делении числа на 3 возможны только три различных остатка: либо 0, либо 1, либо 2.
Если 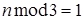 , то
, то 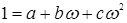 .
.
Если 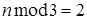 , то
, то 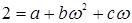 .
.
Если 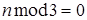 , то
, то  .
.
Решая систему 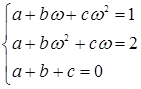 , находим a, b, c.
, находим a, b, c.
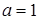 ,
, 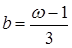 ,
, 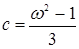 .
.
Итак, получаем следующую формулу:
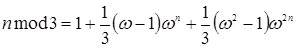 .
.
Задача 14.
Какому необходимому и достаточному условию должно удовлетворять вещественное число  , чтобы равенство
, чтобы равенство  выполнялось при любом вещественном
выполнялось при любом вещественном 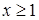 ?
?
Решение:
При любом вещественном 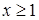 и
и 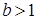 равенство
равенство 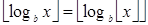 выполняется Û b — целое число.
выполняется Û b — целое число.
Если b — целое число, то функция 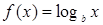 непрерывная, возрастающая функция (так как
непрерывная, возрастающая функция (так как 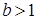 ). Пусть
). Пусть 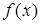 — целое число, т.е.
— целое число, т.е. 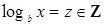 . Тогда
. Тогда 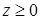 , так как
, так как  и
и 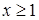 . Выражая
. Выражая 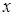 через
через 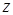 , получим
, получим 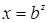 — целое, как натуральное число в неотрицательной целой степени. Поэтому можно применить формулу (6) и получить равенство
— целое, как натуральное число в неотрицательной целой степени. Поэтому можно применить формулу (6) и получить равенство 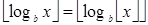 .
.
Если b — не целое число, то при 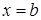 равенство
равенство 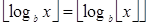 не будет выполняться, так как
не будет выполняться, так как 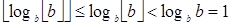
Итак, если 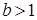 , то равенство
, то равенство 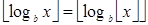 выполняется при любом вещественном
выполняется при любом вещественном 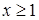 тогда и только тогда, когда b — целое число.
тогда и только тогда, когда b — целое число.
Ответ: b — целое число.
Задача 15.
Найдите сумму всех чисел, кратных x, в замкнутом интервале [ a, b ], при 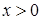 .
.
Решение:
Числа, кратные 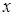 имеют вид
имеют вид 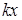 , где
, где 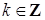 . Нужно просуммировать те из чисел
. Нужно просуммировать те из чисел 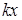 , для которых
, для которых  . Учитывая, что
. Учитывая, что 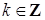 и (4), имеем
и (4), имеем
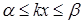 Û
Û 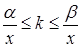 Û
Û 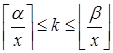 .
.
Нам нужно вычислить следующую сумму:
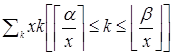 .
.
В этой сумме 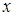 можно вынести за скобки, а в скобке останется сумма всех чисел от
можно вынести за скобки, а в скобке останется сумма всех чисел от 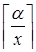 до
до 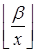 включительно. Применяя формулу арифметической прогрессии получаем:
включительно. Применяя формулу арифметической прогрессии получаем:
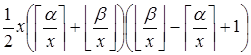 .
.
Задача 16.
Покажите, что n -й член последовательности 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,… равен 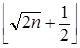 . (Каждое число m входит в данную последовательность m раз.)
. (Каждое число m входит в данную последовательность m раз.)
Решение:
В этой последовательности чисел меньших 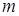 будет
будет 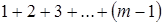 , а чисел не превосходящих
, а чисел не превосходящих 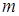 будет
будет 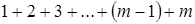 . Поэтому, если xn = m, то
. Поэтому, если xn = m, то
Оценим n:
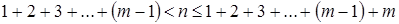 Û
Û
Û 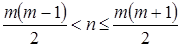 Û
Û
Û 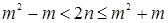 Û
Û
Û 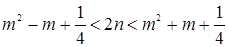 Û
Û
Û 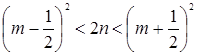 Û
Û
Û 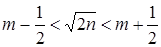 Û
Û
Û 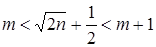 Þ
Þ
Þ 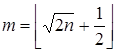 .
.
Следовательно, 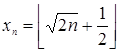 .
.
Задача 1 7.
Найдите и докажите связь между мультимножествами Spec(α) и Spec(α /(α +1)), где α — некоторое положительное вещественное число.
|
|
|
Решение:
Число элементов в Spec(α), которые не превосходят n:
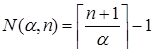 .
.
Число элементов в Spec(α /(α +1)), которые не превосходят n:
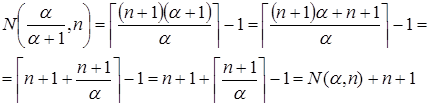 .
.
Итак, получили, что 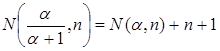 .
.
Покажем на основе этого, что чисел равных 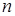 в Spec
в Spec 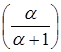 будет на 1 больше, чем в Spec(
будет на 1 больше, чем в Spec(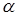 ).
).
При 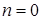 если
если 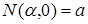 , тогда
, тогда 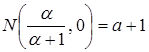 .
.
Пусть в Spec(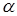 ) элементов не превосходящих
) элементов не превосходящих 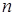 будет
будет 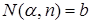 , тогда число элементов в Spec(
, тогда число элементов в Spec(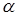 ) равных
) равных 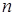 будет
будет 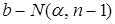 . Подсчитаем количество элементов в Spec
. Подсчитаем количество элементов в Spec 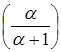 равных
равных 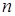 :
:
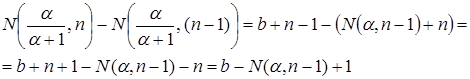
Что и требовалось доказать.
Ответ: чисел равных 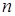 в Spec
в Spec 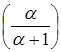 будет на 1 больше, чем в Spec(
будет на 1 больше, чем в Spec(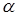 ).
).
Задача 18.
На шахматной доске 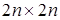 клеток симметрично начерчена окружность с диаметром
клеток симметрично начерчена окружность с диаметром 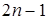 единиц. Через сколько клеток доски проходит данная окружность?
единиц. Через сколько клеток доски проходит данная окружность?
Решение:
Радиус окружности равен 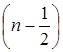 .
.
Горизонтальных прямых, не являющихся сторонами квадрата — ( ).
).
Вертикальных прямых, не являющихся сторонами квадрата — ( ).
).
Окружность каждую из указанных прямых пересекает в двух точках. Она не проходит через углы клеток. Действительно, если предположить, что данная окружность проходит через какой-нибудь угол клетки, то существуют такие целые числа 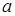 и
и 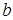 , для которых выполняется теорема Пифагора:
, для которых выполняется теорема Пифагора:  , но
, но 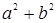 — целое число, а
— целое число, а 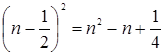 — не целое. Получили противоречие. Следовательно, окружность не проходит через углы клеток.
— не целое. Получили противоречие. Следовательно, окружность не проходит через углы клеток.
Каждую клетку окружность пересекает в двух точках, а каждая точка пересечения принадлежит двум клеткам. Следовательно, окружность проходит через столько клеток доски, сколько имеется точек пересечения её с прямыми: 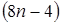 .
.
Ответ: 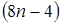 клеток.
клеток.
Задача 19.
Говорят, что f (x) является репликативной функцией, если
f (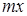 ) = f (
) = f (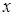 ) + f
) + f 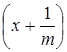 + … + f
+ … + f 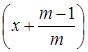
при каждом целом положительном m. Укажите, какому необходимому и достаточному условию должно удовлетворять вещественное число c, чтобы функция f (x) = x + c являлась репликативной.
Решение:
f (x) = x + c — репликативна Û
Û 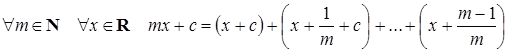 Û
Û
Û 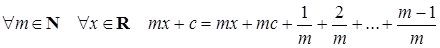 Û
Û
Û 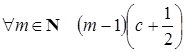 = 0 Û
= 0 Û 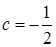 .
.
Ответ: 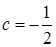 .
.
Литература
Р.Грэхем, Д.Кнут, О.Паташник. Конкретная математика. М.: «Мир» 1998. С 88 - 124.
|
|
|
12 |


